脏污对有砟道床动力特性影响的离散元分析

(北京交通大学轨道工程北京市重点实验室，北京，100044)

有砟轨道是我国铁路的主要结构形式之一，散体道床是有砟轨道的基础，其服役状态是决定线路平稳和安全运营的关键因素[1]。有砟道床由级配道砟组成，其内部存在空隙，随着线路的运营，细小颗粒会侵入道砟颗粒之间的空隙，并逐渐发展成道床脏污现象。脏污改变了道砟颗粒之间的原有接触形式，势必会对有砟道床的服役状态和力学特性产生影响，这直接影响到铁路工务的养护维修及列车的安全运营。因此，针对脏污道床的力学特性研究显得十分重要。既有针对道床脏污的研究大致可以分为试验研究和数值模拟。在试验研究方面，TUTUMLUER等[2]进行了道砟直剪试验，指出脏污会显著降低道床的力学性能，其中对道床抗剪强度的影响最为显著。INDRARATNA 等[3]通过道砟直剪实验分析了土工格栅对脏污道床剪切性能的影响，指出土工格栅能够有效增强道床的抗剪强度。高亮等[4]通过道砟直剪试验分析了不同脏污材质对散体道床剪切力学性能的影响，发现黄沙和煤灰脏污均会显著降低散体道床剪切力学性能，且煤灰对散体道床剪切力学性能的削弱作用比黄沙的更明显。季顺迎等[5-6]基于准静态压缩试验，分析了循环荷载下细沙对铁路道砟弹性模量和沉降量的影响，指出当含沙量较高时，含沙道床的弹性模量会降低而沉降量会增大。INDRARATNA 等[3]通过三轴实验分析了黏土脏污道床的力学性能，指出黏土脏污会降低道床的抗剪强度，不利于道床稳定。FORTUNATO 等[7]开展了三轴实验，指出脏污道床的弹性模量受脏污干湿状态的影响。TRINH等[8]通过三轴试验，分析了路基土侵入有砟道床形成的脏污道床集料在不同含水率下的力学特性，指出当脏污道床的含水率减小时道床的抗剪强度会提高。EBRAHIMI等[9]通过三轴试验，分析了脏污道床在动荷载作用下的变形特性，指出在列车荷载作用下，道床的竖向累计塑性变形随脏污含量的增多而呈线性增加。可以看出，既有针对道床脏污的试验研究多采用直剪试验和三轴试验，虽然试验研究可以获取不同形式脏污道床的抗剪强度、塑性累积变形等宏观参量，但在脏污对道床力学性能影响的细观机理分析方面存在不足。在理论研究方面，徐旸等[10]基于离散单元法进行了道砟直剪试验数值模拟，指出脏污会降低道床的抗剪性能，其下降幅度与道床的脏污程度有关。HUANG等[11]建立了煤灰脏污道床的离散元模型，分析了道床不同位置脏污对其力学性能的影响，指出道床肩部脏污对道床剪切力学性能的影响最大。严颖等[12]采用离散单元法对道砟和细沙颗粒进行建模，分析了不同含沙率对道砟变形模量的影响，结果表明在高含沙率下道床变形模量随含沙率的增加呈线性降低。可以看出人们对道床脏污的理论研究较少，并且其研究也多是停留在对脏污道床的抗剪强度和变形模量等静力分析阶段。另外，就数值模拟方法而言，脏污道床的模拟多采用离散元法，这是由于离散单元法在分析有砟道床这一散粒体结构上存在优势，可以分析颗粒间的相互作用问题，但其他数值模拟方法例如有限单元法等则是将有砟道床模拟为连续体，不能有效地考虑有砟道床的散体特性。综上可知，目前针对道床脏污的研究多围绕道床的抗剪强度等静力学性能，有关脏污对有砟道床动力行为影响的研究鲜有报道，人们对于脏污道床动力特性的认识明显不足，而有砟道床在列车荷载作用下的动力行为直接关系到线路的服役状态及列车的安全平稳运营。基于此，本文作者采用离散单元法建立脏污道床的数值分析模型，对脏污道床的动力特性进行分析，从细观角度揭示脏污颗粒与道砟颗粒之间的相互作用，以期为有砟道床的养护维修提供参考。

1 离散元模型建立

1.1 脏污道床模型的建立

离散单元法通过建立固体颗粒体系的参数化模型，进行颗粒行为模拟和分析，采用局部接触反映宏观问题，可以研究分析颗粒间的相互作用问题、大变形问题等。

道砟颗粒几何特征对其力学特性影响显著，对道砟颗粒几何特性的合理描述是实现有砟道床数值模拟的关键[13]。本文采用图像处理技术获得道砟颗粒的真实外形，并采用圆盘组合的方式获得具有真实外形特征的道砟颗粒离散元模型[14]，如图1所示。

图1 道砟颗粒离散元模型Fig.1 Discrete element model of ballast particle

按照TB/T2140－2018“铁路碎石道砟”[15]中的特级碎石道砟要求生成道床模型，在相应位置生成轨枕，最终建立有砟道床离散元模型，如图2所示。

图2 有砟道床离散元模型Fig.2 Discrete element model of ballast bed

本文选用PFI(percentage fouling index)指标fPFI对道床的脏污程度进行评价，计算公式如下[10]：

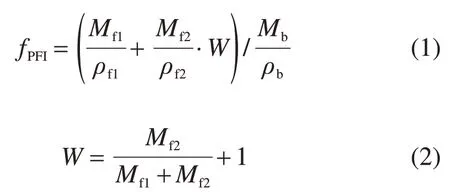
式中：Mf1和ρf1分别为粒径为4.0~9.5 mm脏污的质量与干密度；Mf2和ρf2分别为粒径小于4.0 mm 脏污的质量与干密度；Mb为道砟的质量；ρb为道砟颗粒的干密度。

由于粒径小于4 mm的脏污对道床的力学性能影响更明显[10]，因此，本文采用直径为2 mm 的圆盘单元模拟脏污颗粒。离散元模型中生成道床脏污的过程如下：首先生成随机数(x，y)，当有砟道床离散元模型中在(x，y)位置处生成直径为2 mm的圆盘单元与既有模型不发生重叠时，则生成1个脏污颗粒，若不满足条件则不生成，照此循环以至达到指定的道床脏污率。脏污颗粒生成后在重力作用下重新平衡道床，最终生成的脏污道床的局部模型如图3所示。

图3 脏污道床局部模型Fig.3 Local model of fouling ballast bed

1.2 接触本构的选取

在离散元模型中，接触本构是影响颗粒物质力学特性的重要因素。本文采用线性接触模型定义道砟颗粒之间的接触。

线性接触模型的计算公式如下[16]：

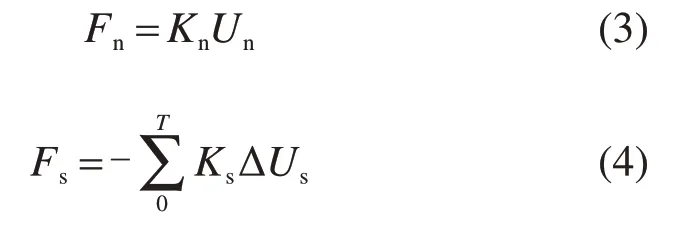
式中：Fn为法向接触力；Kn为接触点的法向刚度；Un为单元之间的法向重叠量；Fs为切向接触力；T为时间；Ks为接触点的切向接触刚度；ΔUs为单元之间切向位移增量。

道砟颗粒之间产生滑动的判别条件为

式中：Fsmax为最大摩擦力，Fsmax=μ|Fn|；μ为摩擦因数。当颗粒之间的切向接触力满足式(5)时，颗粒之间发生滑动，滑动过程中的切向接触力为Fsmax。参考文献[17]，取道床模型的计算参数如表1所示，本文忽略脏污材质的影响，取脏污颗粒的接触参数与道砟颗粒的一致。

表1 离散元模型计算参数Table1 Calculation parameters of discrete element model

1.3 计算工况设置

徐旸等[10]指出，fPFI<30%对应道床轻度污染状态；30%≤fPFI≤70%对应中度污染状态；fPFI>70%对应严重脏污状态。因此，本文设置4种工况的脏污道床并对其动力特性进行分析，见表2。

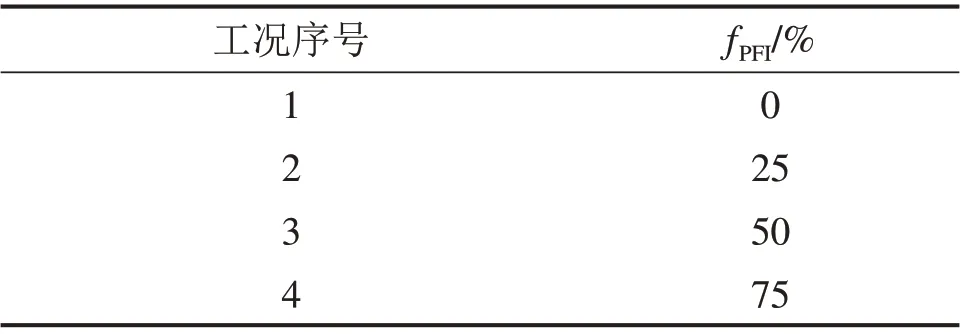
表2 计算工况设置Table2 Calculation conditions details

2 模型验证及荷载施加

2.1 模型验证

将有砟道床在简谐荷载作用下的振动加速度测试结果与离散元模型仿真结果进行对比，验证离散元模型的正确性。张徐等[18]建造了符合我国高速铁路设计规范和施工标准的室内有砟轨道1:1足尺模型，铺设60 kg/m钢轨、弹条V型扣件和混凝土III 型轨枕，轨枕间距为0.6 m，采用特级道砟，枕下道床厚度为0.35 m，道床边坡坡比为1.00:1.75，基床表层厚度为0.7 m。在轨枕的2个承轨槽位置通过液压伺服作动器加载模拟列车荷载作用，对有砟道床在幅值为200 kN，频率分别为2，4 和6 Hz的枕上简谐荷载下的动力响应进行试验研究，测量道床中深150 mm 位置处的道床振动加速度。本文取相同的荷载形式，经平面应变处理后施加在离散元模型的轨枕上，文献[18]测试结果与本文的模型仿真计算结果对比如图4所示。由图4可以看出：道床振动加速度幅值离散元模型仿真计算结果与实测结果较吻合，随着荷载频率的提高而增大的规律也相一致，从而验证了离散元模型的正确性。

2.2 荷载施加

为分析脏污道床在列车荷载作用下的动态响应，参考文献[19]，对轨枕施加的动荷载进行计算：

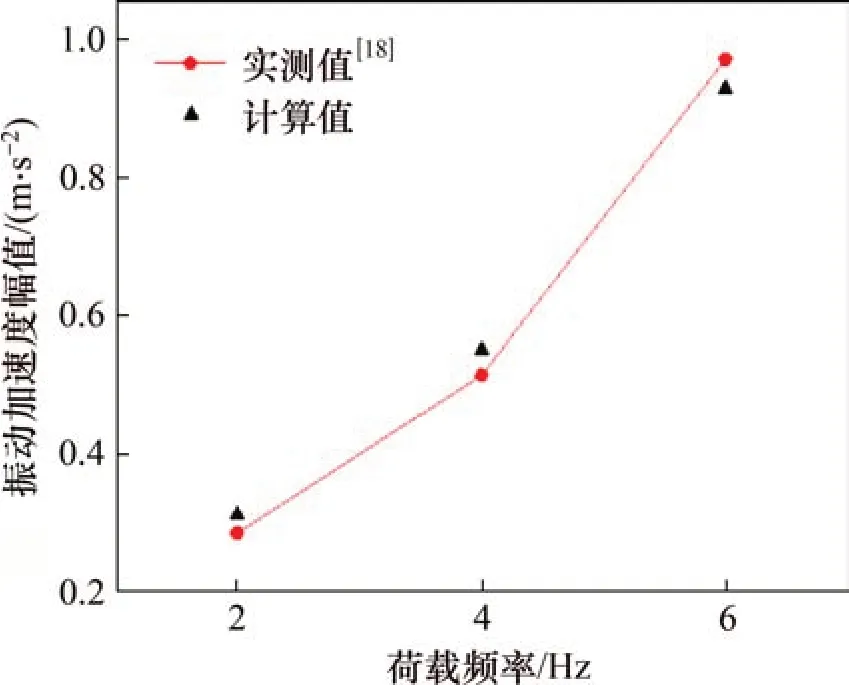
图4 模型振动加速度幅值计算结果与实测结果对比Fig.4 Vibration acceleration amplitude comparisons of model calculation result and field test result

式中：n为车厢节数；v为列车速度，取350 km/h，t为列车荷载作用时间；P0为轮轨作用力，取为96.36 kN[20]；A为常数，其值为单个列车轮轴作用下扣件承受荷载的最大比例，取为0.34；xij为列车轮轴的位置，可以由车辆轴距和定距计算得出，本文列车的轴距和定距分别取为2.5 和17.5 m；w为常数，与单个轮轴荷载的纵向影响范围有关，取为0.76。最终将式(6)计算的枕上荷载经平面应变处理后作为输入荷载施加到模型中。

3 计算结果分析

3.1 脏污对道砟颗粒振动的影响

在仿真计算中对如图5所示位置处的道砟颗粒振动加速度及速度进行监测，此处仅给出工况1和工况4测点处道砟颗粒振动加速度及振动速度时程曲线，如图6所示。由图6可知：工况1 中道砟颗粒的振动加速度和速度幅值分别为1.26g(1g=9.8 m/s2)和4.01 mm/s；工况4中道砟颗粒的振动加速度和速度幅值分别为2.24g和8.60 mm/s，工况4中道砟颗粒的振动加速度和速度较工况1时分别提高了77.7%和114.5%，这说明脏污颗粒会提高道砟颗粒的振动水平。

统计4种工况中测点处道砟颗粒振动加速度和速度的幅值，结果如图7所示。由图7可知：工况1~4中测点处道砟的振动加速度幅值和振动速度的幅值依次增大，且基本呈线性增长趋势。由此可知：在脏污道床中，道砟颗粒的振动加速度和速度受脏污程度的影响，基本上随着道床脏污程度的提高而呈线性增大。

图5 道砟振动加速度测点位置示意图Fig.5 Schematic map of measuring point position of ballast vibration acceleration

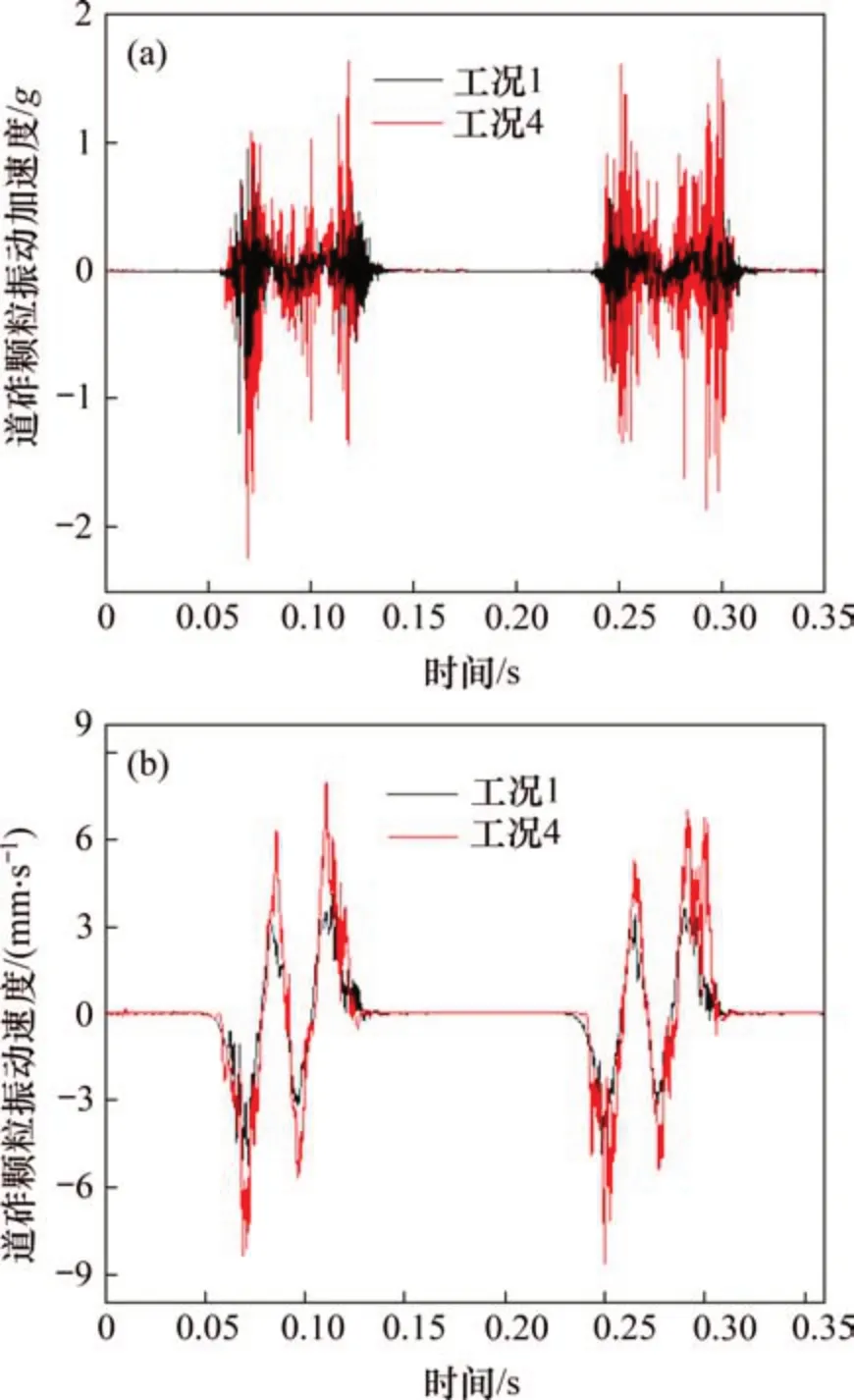
图6 道砟颗粒振动计算结果Fig.6 Calculation results of ballast particle vibration

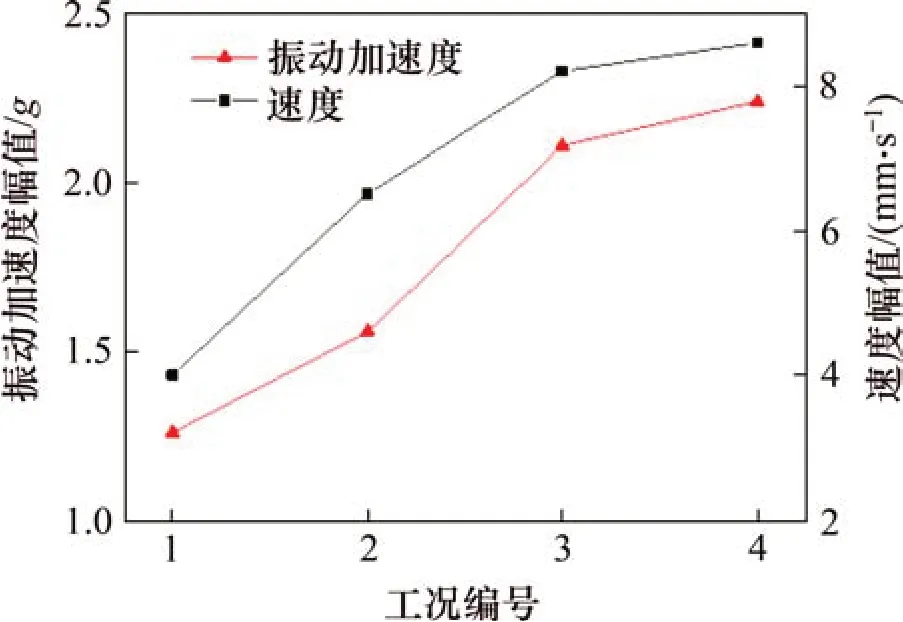
图7 不同工况振动加速度和速度幅值对比Fig.7 Comparison of vibration acceleration and velocity amplitudes under different working conditions

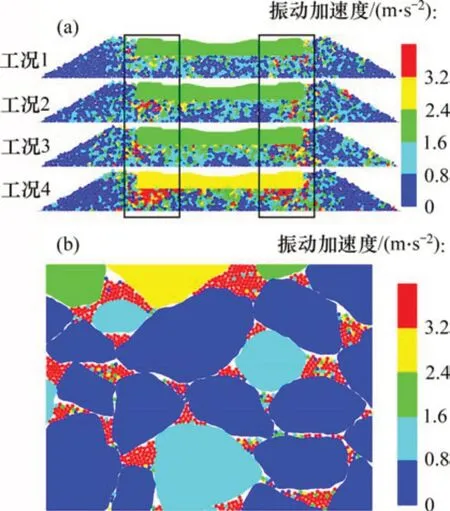
图8 振动加速度云图Fig.8 Nephogram of vibration acceleration

为进一步探究脏污对有砟道床整体振动情况的影响，对列车荷载加载至峰值时刻道床中道砟及脏污颗粒的瞬时振动加速度进行计算，结果如图8所示。由图8(a)可知：当列车荷载加载至峰值时，加速度较大的道砟颗粒主要分布在枕端位置下方区域，且工况1~4中振动幅度较大道砟颗粒的分布区域逐渐扩大，说明脏污对该位置处的道砟振动影响显著，并且脏污颗粒的存在会增大列车荷载对有砟道床的扰动范围；另外，工况4中轨枕的瞬时振动加速度相比工况1~3也有明显提高，说明当道床脏污严重时还会明显地加强轨枕的振动。由图8(b)可知：道砟空隙中脏污颗粒的振动加速度明显大于道砟颗粒的振动加速度，这是由于道砟颗粒在承受枕上动荷载时彼此之间相互咬合，从而使得道砟颗粒之间产生约束作用；而脏污颗粒在道砟空隙中基本处于自由状态，约束较弱从而导致振动水平较高，脏污颗粒的强烈振动对散体道床整体的振动加速度提高起到了促进作用。

3.2 脏污对道砟颗粒受力的影响

为分析脏污颗粒对道砟颗粒受力的影响，根据道砟颗粒之间的接触力计算道砟颗粒的应力状态，道砟颗粒的应力σij计算公式如下[21]：

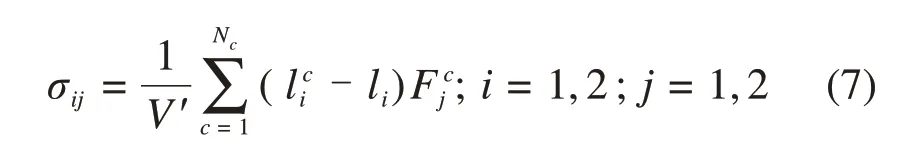
式中：V′为道砟颗粒的体积；Nc为道砟颗粒周围的接触点数；i和j为坐标轴的方向；lci为c接触点的i坐标分量；li为道砟形心的i坐标分量；Fcj为c接触点的接触力在j方向上的分量。

按照式(7)计算列车荷载加载至峰值时道砟颗粒的竖向应力和横向应力，根据道砟颗粒所受应力绘制云图，结果如图9所示。由图9(a)可见：工况1中所受竖向应力较大的道砟颗粒数较少，而工况2~4中道砟颗粒个数明显比工况1的多，并且工况2~4 呈依次增多的规律。图9(b)中有类似的规律，工况1~4中受较大横向应力的道砟颗粒个数依次增多。另外，还可看出整体上道砟颗粒所受的竖向应力大于横向应力，约大1倍。

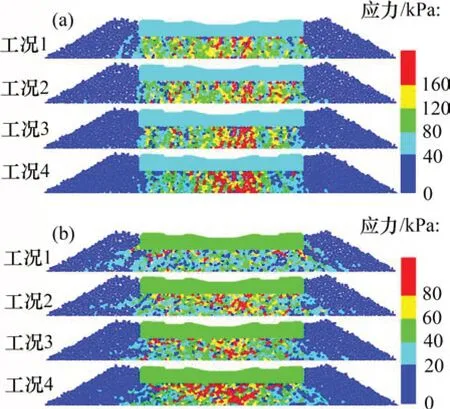
图9 应力云图Fig.9 Stress nephograms

为进一步量化道砟颗粒的受力，统计荷载加载至峰值时道床中道砟颗粒所受的横向应力和竖向应力，结果如图10所示(其中N为道砟颗粒数)。由图10可知：不论是竖向应力还是横向应力，所受应力较小的道砟颗粒数较多；随着应力增大，道砟颗粒的数量逐渐减少，这说明在道床中道砟颗粒的受力并不均匀，仅有小部分道砟承受较大的应力作用。由图10(a)还可看出：当竖向应力大于190 kPa 后，对应同一应力时，工况2~4 的道砟颗粒数比工况1的多，且工况2~4依次增多；由图10(b)可知：当横向应力大于85 kPa 后，对应同一应力时，工况2~4的道砟颗粒数比工况1的多，且工况2~4依次增多。另外，工况2~4中道砟颗粒所受竖向应力和横向应力的最大值均比工况1 的高。由此可知，道床脏污会引起道砟颗粒受力增大，并且脏污越严重对道砟颗粒受力影响越大。

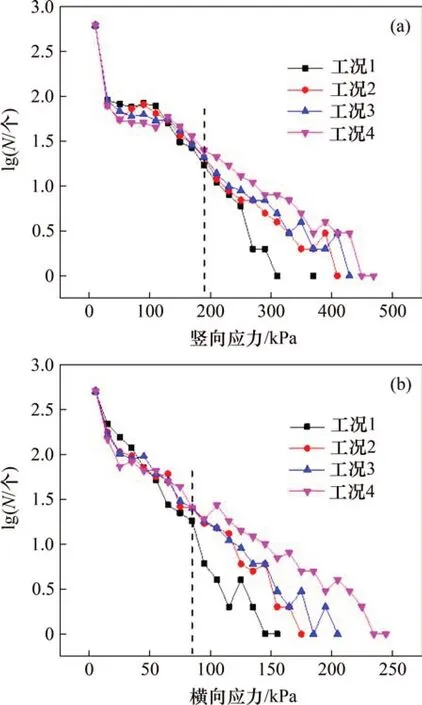
图10 道砟颗粒数与应力的关系Fig.10 Relationship between stress and number of ballast particles

3.3 脏污对道床变形的影响

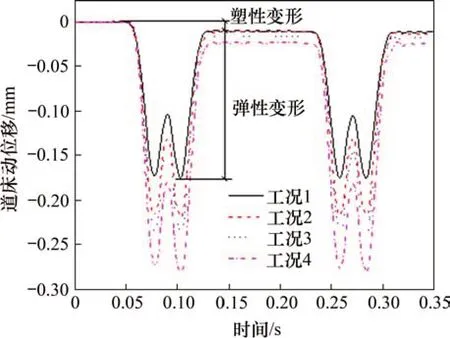
图11 道床变形计算结果Fig.11 Calculation results of ballast bed deformation

本文对列车荷载作用下道床的变形行为进行分析，在仿真计算过程中轨枕底面与道砟颗粒之间始终保持接触，不存在轨枕空吊现象，故本文以轨枕的动位移表征道床的变形行为。记录模型仿真计算过程中轨枕的位移时程，结果如图11所示。由图11可知：在加载过程中有砟道床存在着明显的弹、塑性变形特征。在荷载作用下，道床产生较大的变形，当加载结束后大部分变形以弹性变形的形式得以恢复，但仍留有小部分的塑性变形，在列车荷载重复作用下，这种微小的塑性变形会累积成道床沉降。由图11还可看出：工况1~4 中道床产生的弹性变形依次为0.164，0.203，0.222 和0.254 mm，工况2~4 中弹性变形相比工况1 分别增大23.6%，35.1%和54.9%；加载结束后，工况1~4 中道床产生的塑性变形分别为0.011 5，0.014 8，0.018 9和0.024 2 mm，工况2~4中塑性变形相比工况1时分别增大23.3%，57.5%和101.7%。

将4种工况道床的弹塑性变形绘制成图，如图12所示。由图12可知：列车荷载作用下有砟道床的弹、塑性变形随着道床脏污程度的提高而呈线性增大。

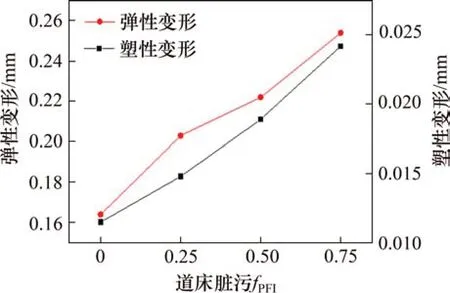
图12 道床变形与脏污程度的关系Fig.12 Relationship between ballast bed deformation and fouing degree

脏污引起道床变形增大的原因主要是脏污颗粒的存在改变了道砟颗粒之间的接触形态，如图13所示。由图13(a)可知：在正常的洁净道床中，道砟颗粒处于点接触状态，在咬合和表面摩擦作用下，在接触点位置处传递接触力；而当道砟颗粒之间存在脏污时(见图13(b)和(c))，在外荷载作用下，脏污颗粒会迁移到道砟颗粒接触点附近从而改变道砟颗粒的接触状态，使得道砟颗粒原本紧密的接触之间产生间隙，道砟之间通过脏污颗粒传力，这不仅破坏了道砟颗粒之间的咬合作用，而且使得原本的咬合和滑动摩擦传力变成了道砟颗粒与脏污颗粒之间的滑动摩擦以及脏污颗粒的滚动摩擦传力，导致道床的稳定性降低，从而在列车荷载作用下产生更大的变形，且在卸载后留有更多的塑性变形，列车荷载长期作用下导致道床产生沉降。另外，在实际线路中，不同里程位置处道床的脏污程度不尽相同，长期运营易使线路产生不均匀沉降。

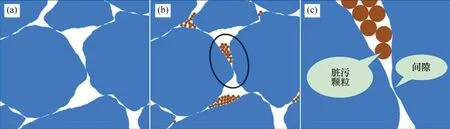
图13 道床离散元模型局部接触Fig.13 Local contact of ballast bed discrete element model

4 结论

1)脏污会提高有砟道床在列车荷载作用下的振动速度及加速度，且二者基本上随着道床脏污程度的提高而呈线性增大；脏污颗粒所受约束较弱，其振动水平高于道砟颗粒振动水平，对道砟振动的提高有促进作用。

2)道床中道砟颗粒所受的竖向应力比横向应力约大1倍，脏污会增大道砟颗粒受力，增加道床中所受较大竖向应力和横向应力道砟颗粒的数量，且脏污越严重对道砟受力影响越明显。

3)脏污会削弱道砟颗粒之间的咬合作用，增大列车荷载作用下道床的变形。道床的弹性变形和塑性变形均随着道床脏污程度的提高而线性增大；脏污不利于道床稳定，易导致线路产生不均匀沉降。