乳制品冷链物流配送中心选址及配送路径优化
王金妹 尹显龙
(福州大学经济与管理学院, 福建福州 350108)
引言
随着国民经济的发展和人们生活水平的提高,乳制品的需求量越来越大。由于乳制品(特别是低温巴氏奶)具有含水量高、保质期短、鲜活性强等特点,且在整条乳制品冷链物流中,配送过程是处于非冷库环境中保护时间较长的一个环节。因此,如何提高乳制品冷链物流配送效率,降低乳制品发生变质的风险,成为乳制品冷链物流研究的关键。近年来,国内乳制品冷链物流发展迅速,但仍存在较多问题,如配送路径不合理、配送效率低、乳制品变质、难以满足客户时间窗等,都在一定程度上制约乳制品行业的发展。乳制品冷链物流配送中心选址及配送路径优化是乳制品冷链物流配送网络建设中的关键环节,合理的配送中心选址及路径规划不仅能提高乳制品冷链物流的运作效率,而且能优化整个供应链网络,从而进一步达到成本最小和效益最大化的目的,保证乳制品冷链物流体系的平稳发展。因此,如何确定乳制品冷链物流配送中心的合理位置,并进一步从整个配送系统的角度对配送路径进行优化,构建有效合理的冷链物流网络配送系统,对于冷链配送企业具有重要意义。
当前,关于乳制品的既有研究主要集中在乳制品供应链构建、质量安全、配送模式、运输组织模式、选址及配送路径规划等方面。在乳制品供应链方面,王爽提出了包含内部和外部供应链的理想型运营机制。[1]Tordecilla-Madera等确定了乳制品供应链的最优配置方案和相关成本。[2]Kim提出了冷链供应链的智能风险管理框架。[3]在乳制品质量安全方面,陈梅和茅宁以乳制品为例,验证了战略性原料投资治理模式的相关影响因素。[4]Moncayo等运用激光诱导分解光谱(LIBS)技术对劣质奶进行了定量和定性分析。[5]在乳制品冷链物流配送模式方面,Reiner等得出不同策略和混合存储格式对物流运作流程效率具有较大影响。[6]张建军构建了可视化供应链配送模式。[7]在冷链物流的运输组织模式方面,Wu等首次提出了评价水产品冷链物流绩效的SISP模型和ACSSN模型。[8]在配送中心选址方面,Lee和Lee等建立了确定配送中心位置和客户分配的广义分层覆盖定位问题的混合整数规划模型,通过禁忌搜索算法取得了良好的求解效果。[9]杨晓芳等对冷链物流中的产品新鲜度进行研究,假设客户满意度主要依赖产品新鲜度和服务时间,进而使用具体算例寻求多目标优化问题。[10]在配送路径规划模型求解算法方面,缪小红等构建了单一冷链配送中心、多客户的冷链物流配送模型,研究表明采用改进的遗传算法更易获得最优解。[11]Errico等研究了考虑硬时间窗和随机服务时间的车辆路径问题,开发了一种准确计算线路成功概率的方法,通过分支切割算法实现对问题的求解。[12]Sarasola等对具有随机需求和动态的车辆路径问题进行了研究,提出了可变邻域搜索算法(VNS),研究表明该算法在求解该车辆路径问题时具有明显的优势,能够获得动态的最小偏差。[13]Silvestrin和Ritt采用禁忌启发式算法对多配送车辆路径问题进行求解。[14]杨玮等研究了基于货架寿命的乳制品配送车辆路径优化问题,并设计了自适应交叉变异的改进遗传算法进行求解。[15]
以上研究成果为乳制品冷链配送中心选址及路径优化研究指明了方向,但现有文献对乳制品冷链物流配送中心选址和路径优化的综合研究仍相对缺乏。虽然部分学者有对单一的乳制品配送中心选址问题或单一的冷链配送路径规划问题进行研究,但未能综合考虑乳制品的特殊性及其配送过程中各个环节的成本结构。基于此,本文充分考虑乳制品的特点,通过系统分析乳制品冷链物流配送过程中各个环节的成本结构,将乳制品冷链物流配送中心选址及配送路径优化问题作为一个组合优化问题进行研究,以期为乳制品相关企业提供一定的理论借鉴和现实指导。
一、问题描述
本文研究带时间窗的乳制品冷链物流配送中心选址及配送路径优化问题。为了研究方便,只考虑由单一生产商、若干个配送中心和若干个零售商组成的三级配送网络,其中由于生产商与配送中心之间运输量较大,采用干线运输,即乳制品是直接从生产商运送至配送中心;而由于配送中心与零售商之间的配送具有需求量小、客户分布分散等特点,采用巡回送货方式对零售商进行配送,以降低配送成本。
结合乳制品的特点及相关理论,将乳制品配送中心选址和路径规划作为组合优化问题进行研究,上层战略目标与下层战术目标具有相互影响关系,上层战略目标确定配送中心选址,选址影响下层配送路径的规划,反过来配送路径不断优化可以确定其配送线路所需的最佳配送中心的位置,由此不断相互影响最终确定最佳的配送中心位置及配送线路(见图1)。本文在分析各环节的成本结构时,上层主要考虑配送中心的建设成本、车辆固定成本和运输成本、货损成本、制冷成本;下层主要考虑货损成本、惩罚成本、制冷成本、车辆固定成本和运输成本,旨在通过合理地分析乳制品配送网络中各项影响因素来确定最佳的选址与配送路径方案。
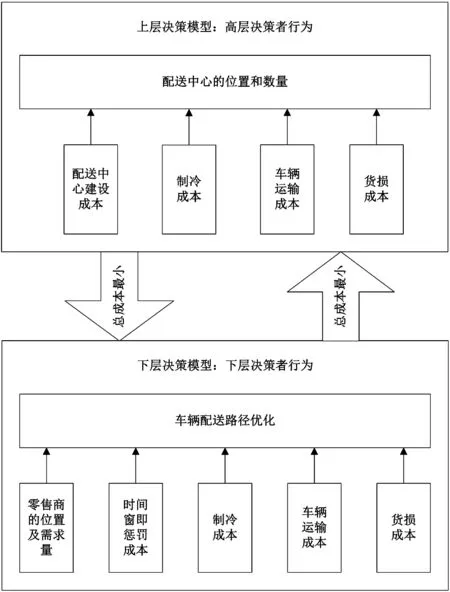
图1 双层规划模型结构
二、模型假设
本文研究的问题是乳制品冷链物流配送中心选址和配送路径规划这一组合优化问题。由于该问题属于NP-Hard问题,为了研究方便,降低计算难度,对模型提出以下假设:
假设1 只考虑一个生产商和六个备选配送中心并且其坐标已知,零售商的位置和需求量已知。
假设2 运输车辆有A种车型,每一种车型的参数都相同。
假设3 每辆车只属于一个配送中心,每辆车服务多个零售商并返回配送中心。
假设4 配送中心每天的额定处理量可以满足零售商的需求。
假设5 运输费用与运输距离成正相关。
假设6 生产商到配送中心采用干线运输,配送中心到零售商采用巡回运输。
假设7 零售商的需求量从配送中心得到满足,不存在零售商之间的相互调配。
假设8 配送中心到零售商的单位运输费用固定,不考虑距离经济理论的影响。
假设9 运输途中不考虑车辆故障、道路堵塞、天气影响等因素。
假设10 末端零售商的位置、需求量等已知,且都有时间窗限制、惩罚成本与时间存在线性关系。
假设11 每种车型的车辆在中途的运输过程中速度保持恒定。
三、模型构建
(一)符号及变量说明
M:表示生产商;
D={i|i=1,2,3,…,d},表示备选配送中心的集合;
R={j|j=1,2,3.…,r},表示零售商的集合;
H=D∪R,表示所有节点的集合;
L={l|l=1,2,3,…,L},表示第l辆运输车辆或者第l条配送路线;
Ci:表示在i处建立配送中心的成本,本文将该成本转化成每天的折旧费;
Xi:0,1变量,表示在i处建立配送中心时为1,否则为0;
dmi:表示生产商M到配送中心Di的距离;
dij:表示配送中心Di到零售商Rj的距离;
djk:表示零售商Rj到零售商Rk的距离;
P:表示单位制冷成本;
P1:表示单位重量的产品价格;
tmi:表示产品从生产商M到配送中心Di的运输时间;
ti:表示产品停留在配送中心Di的处理时间;
tij:表示产品从配送中心Di到Rj的运输时间;
tj:表示产品在零售商Rj的服务时间(即卸货时间);
tjk:表示产品从零售商Rj到零售商Rk的运输时间;
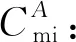

Cl:表示车辆l的固定使用成本;
Zl:0,1变量,其中第l辆运输车辆被使用时为1,否则为0;
Zikl:0,1变量,若第l辆运输车辆从配送中心Di向零售商Rk配送即为1,否则为0;
Yik:0,1变量,若零售商Rk由配送中心Di配送即为1,否则为0;
Ql:表示车辆l的运载量;
Qi:表示配送中心Di的存储容量;
qj:表示零售商Rj的需求量;
qi:表示配送中心Di的需求量;
Pj:表示零售商Rj的惩罚成本;
Wmi:表示产品的初始重量;

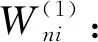

α:表示车辆车厢的劣化程度;
R2:表示热传导率,单位为w/(m2·k);
Sl:表示车辆l的车体平均表面积;
ΔT:表示车厢内外温度差,单位为K;
Vl:表示车辆l的车厢体积;
β:表示车辆开门程度系数;
Uj:0,1变量,表示零售商的时间窗得到满足为1,否则为0;
f1、f2、f3:分别表示生产商到配送中心的货损成本、配送中心内部操作时的货损成本、配送中心到零售商的货损成本;
f4、f5、f6:分别表示生产商到配送中心的运输成本、配送中心到零售商的运输成本、生产商到配送中心以及配送中心到零售商使用车辆时的固定成本;
f7、f8:分别表示生产商M到配送中心Di的运输途中消耗的制冷成本、配送中心Di到零售商Rj的运输途中消耗的制冷成本;
f9、f10:分别表示在配送中心Di进行装卸搬运作业时的制冷成本、在零售商装卸搬运作业的制冷成本。在货物装卸搬运过程中,冷链配送车厢内外会发生冷热空气交换,为简化问题,装卸搬运时的制冷成本可通过计算车门的热交换进而计算消耗的制冷剂成本而获得[16];
f11、f12:分别表示配送中心的建设费用、违背零售商最佳服务时间的惩罚成本。
(二)双层规划模型构建
在传统模型中,通常将配送中心选址和路径规划问题作为两个相对独立的子问题,即在确定配送中心选址方案的基础上,进行配送路径的规划。然而,由于配送中心选址与路径规划是两个层级的决策目标,上层选址问题的优化目标值与下层路径规划目标值之间存在一定的主导和从属关系,该组合优化问题是主从递阶决策问题,具有一定的层次决策和嵌套结构关系,符合双层规划模型的结构特征。因此,本文将双层规划模型融入到乳制品冷链物流配送中心选址和路径规划的组合优化问题的研究中,即上层为选址优化模型,下层为路径优化模型,从而形成相互影响、动态优化的双层规划模型。在该双层规划模型中,上层模型和下层模型都具有各自的目标函数和约束条件,上层决策者在决策变量值(Xi)的同时也影响下层决策者,限制下层决策者的可行性约束级,而下层模型的决策变量(如Zikl)又反过来影响上层决策。
1. 上层模型
在乳制品冷链物流网络配送系统中,配送中心选址问题是冷链物流网络优化的一项重大决策。本文主要考虑乳制品生产商到配送中心的运输成本、配送中心的建设成本、制冷成本、货损成本、车辆固定成本,构建了以配送中心选址费用最低为决策目标的上层规划模型,如下:
s.t.

(2)

(3)
Xi=0,1;i∈D
(4)
其中: 公式(1)表示配送中心选址总成本最小,公式(2)表示乳制品冷链物流网络中至少建立一个配送中心;公式(3)表示配送中心的容量能够满足
零售商的需求;公式(4)表示是否在i处建立配送中心,当在i处建立配送中心时为1,否则为0。
2. 下层模型
乳制品从生产商运输到配送中心后,配送中心要根据零售商的交通状况、地理位置、需求量以及零售商的时间窗进行合理的路径规划,从而提高顾客满意度,降低配送中心的运营成本。下层的配送路径规划模型如下:
s.t.

(6)

(7)

(8)
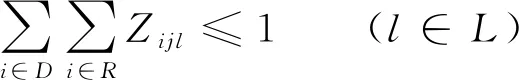
(9)

(10)
ETj≤Tj≤LTj
(11)
Uj=0,1 (j∈R)
(12)
Zl=0,1 (l∈L)
(13)
Zikl=0,1 (i∈D,k∈R,l∈L)
(14)
Yik=0,1 (i∈D,k∈R)
(15)
其中:公式(5)表示双层规划模型中的下层目标函数,总成本涵盖配送中心内部操作的货损成本、配送中心到零售商的固定成本、货损成本、制冷成本、运输成本和惩罚成本;公式(6)表示一个零售商只由一辆配送车进行配送;公式(7)表示配送车辆的运输量不能超过其最大载重量;公式(8)表示每辆车采取巡回配送方式,即车辆到达一个零售商之后,再从这个零售商出发进入下一个零售点;公式(9)表示不存在各个配送中心调派车辆的情况;公式(10)表示任意两个配送中心不存在配送关系;公式(11)表示配送车辆到达零售商的时间限制;公式(12)、公式(13)、公式(14)及公式(15)均表示相应变量为0,1变量。
四、求解算法
本文在研究乳制品冷链物流配送中心选址及配送路径规划组合优化问题中,运用双层规划模型来描述配送中心选址与路径规划之间的动态相互影响关系,试图通过改变乳制品冷链物流配送中心的位置来影响配送路径的最佳方案,而配送路径方案不断优化又反过来影响配送中心的最佳位置。这种相互择优的不断迭代、不断优化的过程计算量大,计算难度复杂,并且可选择的选址与路径规划组合方案众多。由于遗传算法具有较好的寻优过程,并且该算法具有较好的稳定性,能够全局性搜索各种可能的组合方案,从中选出最优,适合双层次规划模型中对计算量的要求,所以本文选择遗传算法对乳制品冷链物流配送中心选址及配送路径优化问题进行求解。具体步骤如下:
Step1 根据优化问题中决策参数的特征,确定决策参数的编码规则,设置染色体的编码长度,完成对参数的编码操作。
Step2 初始化种群,产生一组随机初始解,初始解的个数即为种群规模。
Step3 计算种群中每个个体的目标函数以及各个个体的适应度,判断个体的优劣程度,如果满足条件就输出该个体,否则进入第Step4步。
Step4 选择:选择适应度大的个体,淘汰适应度小的个体。
Step5 交叉:根据一定的方式和概率模拟生物界的遗传规律进行个体交叉得到新个体。
Step6 变异:根据小概率事件变异产生新个体。
Step7 根据Step5和Step6产生的新个体返回Step3。
五、算例分析
(一)基础数据
本文对范围为10000平方公里的区域进行研究,由于具体数据的可获得性问题,在参考已有相关文献的基础上进行了合理假设,假设该区域内有1个乳制品生产商(M)、6个备选乳制品配送中心(Di,i=1,…,6)以及40个零售商(Rj,j=1,…,40)。假设乳制品生产商的生产能力可以满足乳制品配送中心及零售商的需求,其坐标已知;备选乳制品配送中心的日处理量为30吨,设计使用年限为30年,其坐标已知;备选乳制品配送中心的建设成本已知(为简化问题,本文不考虑折旧率,将配送中心的建设成本线性平均分摊成每天的折旧费用);零售商的坐标、需求量、时间窗已知。生产商、配送中心、零售商参数、车辆基本参数如表1至表4所示。

表1 生产商及配送中心参数

表2 零售商参数
续表2

零售商坐标需求量(kg)客户要求时间窗客户接受时间窗服务时间(分钟 )8(4.68,50.4)904(5:50-7:10)(5:30-7:30)209(90.12,76.68)724(4:40-7:15)(3:40-7:30)2010(95.74,76.3)1060(4:00-6:30)(2:50-7:00)2011(87.68,71.88)852(4:30-6:50)(3:30-7:00)2012(82.28,54.82)684(4:10-7:00)(4:00-7:20)2013(85.12,42.04)788(4:50-6:45)(4:30-7:00)2014(65.88,64.9)936(4:30-6:25)(3:30-6:45)2015(5.6,24.5)900(4:50-7:30)(3:30-7:50)2016(68.6,68.02)780(4:00-6:20)(3:50-6:35)2017(75.64,54.48)820(4:50-7:20)(3:30-8:30)2018(70.12,45.73)932(3:50-6:45)(2:30-7:00)2019(10.64,34.75)720(5:20-7:30)(4:30-7:40)2020(20.35,29.87)868(3:20-6:30)(2:30-6:50)2021(25.46,7.95)1156(3:30-6:35)(2:30-7:00)2022(65.67,17.84)780(3:30-6:00)(2:30-6:30)2023(85.94,15.73)624(5:50-8:30)(4:40-8:40)2024(19.27,59.24)1168(4:15-6:50)(3:00-7:00)2025(30.59,72.34)1092(5:30-7:40)(4:20-7:50)2026(38.96,84.38)1012(4:30-7:20)(3:40-7:30)2027(60.48,39.76)900(6:00-8:30)(5:00-8:55)2028(20.47,48.72)604(4:50-6:55)(3:30-7:00)2029(15.68,10.57)904(3:50-6:50)(2:50-7:15)2030(40.59,15.86)608(4:50-7:30)(3:40-7:50)2031(54.71,18.94)952(4:50-6:20)(3:30-6:30)2032(75.37,2.69)624(5:00-6:50)(4:30-7:00)2033(43.61,69.87)1152(6:00-8:30)(4:30-8:40)2034(97.65,98.45)992(5:50-8:30)(4:50-8:55)2035(60.36,94.65)832(3:35-6:10)(2:30-6:40)2036(47.95,96.74)872(3:40-5:50)(2:30-6:00)2037(3.72,5.38)372(4:40-7:20)(3:30-7:30)2038(91.24,30.17)1176(3:30-5:30)(2:30-6:00)2039(85.14,90.67)1052(4:50-5:10)(3:40-5:55)2040(52.4,41.96)692(5:50-6:20)(4:30-6:30)20

表3 其他参数的基本数据

表4 车辆基本参数
(二)算例求解
利用MATLAB2014对所构建的乳制品双层规划模型进行求解,其中遗传算法中设置初始种群规模为100,种群的迭代次数为200,交叉概率为0.8,变异概率为0.3。为了进一步证明该双层规划模型的正确性和遗传算法的有效性,运用遗传算法分别对该组合优化问题和两个独立子问题进行求解。为了保证两组结果具有可对比性,选址和配送路径规划这两个独立子问题的数学模型所考虑的成本因素与双层规划模型相同,但两个子问题之间是相对独立的。
1. 组合优化问题的求解结果
在双层规划模型中,由于配送中心选址和路径优化之间存在动态影响、相互择优的关系。运用MATLAB软件编程,运行得到的结果如图2,双层规划模型最优目标迭代过程见图3。

图2 双层规划模型的求解结果
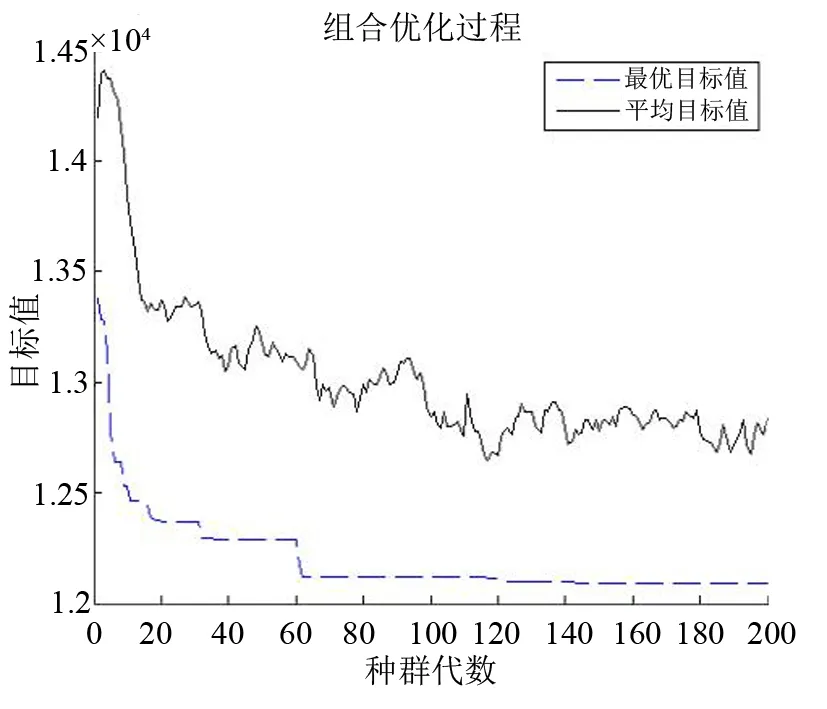
图3 双层规划模型最优目标迭代
由运行结果可知:
(1)由图1可知,在6个备选配送中心选中,由D3、D4这两个配送中心对40个零售商进行配送。D3有8条配送路径,其中6条采用2.5吨冷藏车进行配送,其余2条采用3.5吨冷藏车进行配送;D4有6条配送路径,其中4条采用2.5吨冷藏车进行配送,其余2条采用3.5吨车型进行配送。另外生产商到配送中心D3和D4采用10吨的车型进行干线运输。
(2)由图2可知,当迭代次数大于140次之后,目标值趋于稳定,最优的目标值为12104.52元。同时表明,遗传算法对于求解乳制品冷链物流配送中心选址及配送路径优化双层规划模型具有良好的收敛性。
(3)根据配送中心对零售商配送的路径安排、各个配送中心到零售商之间的距离以及在停留在零售商的服务时间,假设每辆冷藏车从各个乳制品冷链配送中心出发的时间点均为3∶00,则可进一步计算出每条路径中配送车辆到达各个零售商的时间点。计算结果显示,其中7个零售商的配送时间没有在最佳的时间窗送达,但仍处于这些零售商可接受的时间窗范围内。
2. 独立子问题的求解结果
将乳制品冷链物流配送中心选址和配送路径规划作为两个相对独立的子问题分别进行求解,即先对乳制品冷链物流配送中心选址子问题进行求解,在确定配送中心选址方案的情况下,再对配送路径规划子问题进行求解。其他参数设置、约束条件及算法设计均与上一节相同。实验结果得到的配送中心选址及配送路径见图4,配送中心选址优化迭代过程见图5,寻求最优目标迭代过程见图6。
由运行结果可知:
(1)由图4可知,在6个备选配送中心选中,由D3、D5这两个配送中心为40个零售商提供配送服务。D3有5条配送路线,其中3条采用2.5吨冷藏车进行配送,1条采用3.5吨冷藏车进行配送,1条采用5吨冷藏车进行配送;D5有9条配送路线,其中7条采用2.5吨冷藏车进行配送,其余2条采用3.5吨车型进行配送。另外,生产商到配送中心D3采用10吨和5吨的车型进行干线运输,生产商到配送中心D5采用10吨的车型进行干线运输。

图4 独立子问题的求解结果

图6 独立子问题的最优目标迭代
(2)由图5可知,对当种群迭代次数大于10次之后,配送中心选址优化目标值趋于稳定,最优选址方案的目标值为3985.64元。
(3)由图6可知,当种群迭代次数大于100次之后,考虑独立子问题的最优目标趋于稳定,最优方案的目标值为12625.64元。
3. 结果对比分析
根据上述求解过程,得到两类问题的求解结果,如表5所示。
通过上述分析,在总成本方面,组合优化问题中每天的总成本为12104.52元,独立子问题每天的总成本为12625.64元,表明按照组合优化问题求解的乳制品冷链物流配送中心选址及配送路径方案每年能为乳制品企业节省190208.8元。对比结果进一步证明了双层规划模型的合理性和遗传算法的有效性。

表5 两类问题求解结果
六、结论
本文依据乳制品的特点,系统分析乳制品冷链物流配送过程中各个环节的成本结构,将乳制品冷链物流配送中心选址及配送路径优化问题作为一个组合优化问题进行研究,从而构建了更贴近实际情况的双层规划模型;并针对模型的具体特点,采用遗传算法对该模型进行求解。得出以下结论:
(1)在模型构建方面,针对带软时间窗的乳制品配送中心选址和路径规划的双层规划问题,将上层选址和下层路径规划作为一个组合优化问题进行研究更加贴近现实情形。
(2)在算法求解方面,具有较强全局搜索能力的遗传算法对乳制品配送中心选址和配送路径组合优化问题求解具有较好的收敛性。
(3)在算例分析方面,通过对比双层规划模型求解结果和配送中心选址及配送路径优化两个子问题的求解结果,发现将乳制品冷链物流配送中心选址及配送路径规划作为一个组合优化问题能够更好地达到整体最优的状态。
由于现实中的乳制品配送中心选址和路径优化问题比较复杂,本文仍存在一些不足之处,如本文假设两个节点之间为直线距离,而在现实的配送网络中,任意两点之间的实际配送距离往往与直线距离不一致,这将是下一步研究的重点。
注释:
[1] 王 爽:《我国乳品业供应链运营模式研究》,硕士学位论文,天津大学,2008年。
[2] Tordecilla-Madera R.,Polo A.,Muoz D.,et al.,“A robust design for a colombian dairy cooperative's milk storage and refrigeration logistics system using binary programming”,InternationalJournalofProductionEconomics,vol.183,no.3(2016),pp.710-720.
[3] Kim K.,Kim H.,Kim S. K.,et al., “An intelligent risk management framework for context-aware ubiquitous cold chain logistics”,ExpertSystemswithApplications,vol.46,no.15(2016),pp.463-473.
[4] 陈 梅、茅 宁:《不确定性、质量安全与食用农产品战略性原料投资治理模式选择——基于中国乳制品企业的调查研究》,《管理世界》2015年第6期。
[5] Moncayo S.,Manzoor S.,Rosales J. D.,et al.,“Qualitative and quantitative analysis of milk for the detection of adulteration by Laser Induced Breakdown Spectroscopy (LIBS)”,FoodChemistry,vol.232(2017),pp.322-328.
[6] Reiner G.,Teller C.,Kotzab H.,“Analyzing the efficient execution of in-store logistics processes in grocery retailing—the case of dairy products”,Production&OperationsManagement,vol.22,no.4(2013),pp.924-939.
[7] 张建军:《生鲜乳制品冷链物流模式评价及构建研究》,《技术经济与管理研究》2015年第11期。
[8] Wu W.,Deng Y.,Zhang M.,et al., “Performance evaluation on aquatic product cold-chain logistics”,JournalofIndustrialEngineering&Management,vol.8,no.5(2015),pp.1746-1768.
[9] Lee J M.,Lee Y. H.., “Tabu based heuristics for the generalized hierarchical covering location problem”,Computers&IndustrialEngineering,vol.58,no.4(2010),pp.638-645.
[10] 杨晓芳、姚 宇、付 强:《基于新鲜度的冷链物流配送多目标优化模型》,《计算机应用研究》2016年第4期。
[11] 缪小红、周新年、林 森,等:《第3方冷链物流配送路径优化研究》,《运筹与管理》2011年第4期。
[12] Errico F.,Desaulniers G.,Gendreau M.,et al., “The vehicle routing problem with hard time windows and stochastic service times”,EuroJournalonTransportation&Logistics,vol.9,no.1(2016),pp.1-29.
[13] Sarasola B.,Doerner K. F.,Schmid V.,et al., “Variable neighborhood search for the stochastic and dynamic vehicle routing problem”,AnnalsofOperationsResearch,vol.236,no.2(2016),pp.425-461.
[14] Silvestrin P. V.,Ritt M., “An Iterated Tabu Search for the Multi-compartment Vehicle Routing Problem”,Computer&OperationsResearch,vol.81(2017),pp.192-202.
[15] 杨 玮、赵 晶、张 堃,等:《基于货架寿命的乳制品配送车辆路径优化研究》,《包装工程》2019年第11期。
[16] 康景隆:《食品冷藏链技术》,北京:中国商业出版社,2005年。
- 福州大学学报(哲学社会科学版)的其它文章
- 中文网络评论的隐式产品特征提取方法研究
- 创业型人才与创新型人才心理特质对照研究

