基于差异节点集的加权频繁项集挖掘算法
王 斌,房新秀,魏天佑
(青岛理工大学 信息与控制工程学院,山东 青岛 266520)
0 概述
自AGRAWAL提出关联规则[1-2]以来,关联规则挖掘[3-4]引起相关学者的广泛关注。传统的关联挖掘算法通常忽略数据库中各个项目重要程度的区别,而在分析实际数据时,利用加权关联规则[5-6]能够发现出现频率较低但权值较大的重要频繁项集。加权数据库往往出现在真实的应用程序或智能系统中,如销售数据库、股票数据库、文本数据库以及医疗数据库等。
文献[7]较早提出加权频繁项集挖掘(WFIM)算法,该算法使用平均函数来评估权重的一个项目集。研究人员根据加权对象的不同,将加权频繁模式挖掘方法分为两类。一类为高效用项集的挖掘[8],如EFIM[9]、MHUI[10]等算法,其考虑项的数量和权重大小,但是,该类算法在挖掘频繁项集时进行了多次重复的计算,降低了挖掘的效率。另一类考虑项的权重信息,如PWAI[11]、IWS[12]和FWI-WSD[13]等算法,其根据项集的加权支持度来确定加权频繁项集,该类算法广泛应用于挖掘加权频繁闭项集[14]、加权可消除模式挖掘[15]、加权最大频繁项集[16]等任务中。但是,上述算法需要多次扫描数据库或多次遍历树结构来挖掘FWIs[17],因此,在挖掘效率方面仍然存在一定不足。
文献[18]提出了一种基于WN-list的算法NFWI,其采用WN-List数据结构,该数据结构是N-List[18]的扩展。NFWI算法用于大型稀疏的数据集时性能良好,但是在密集数据集中,由于WN-list需要前序编码和后序编码来表示节点,因此NFWI需要进行大量的交集运算,从而降低了挖掘效率。
文献[19]提出一种最大频繁项集挖掘算法DNMFIM,其采用DiffNodeset[20]数据结构,本文在该数据结构中加入权值得到WDiffNodeset数据结构。针对NFWI算法挖掘效率低的问题,本文提出一种使用WDiffNodeset数据结构的加权频繁项集挖掘算法DiffNFWI。该算法采用集合枚举树和混合搜索策略相结合的方法查找加权频繁项集,利用差集策略计算项集的加权支持度。在此基础上,采用集合枚举树生成加权频繁项集,并通过剪枝策略修剪搜索空间。
1 相关定义与问题描述
1.1 相关定义
定义1事务权重tw(tk)指加权数据库(WD)记录事务tk中各项目权重的平均值[18],即为:
(1)
其中,|tk|是事务中项目的总数。
定义2项集X的加权支持度ws(X)是包含该项目的事务权重与总事务权重的比值[18],即为:
(2)
其中,t(X)是包含X的事务集。
定义3∀i1,i2∈F1,F1是一系列频繁项集,当且仅当ws(i2)>ws(i1),有i2>i1。
定义4∃i1i2…ik,L1={ik,…,i2,i1},L1为有序的加权频繁项集,并按照加权支持度降序排列。
1.2 加权节点树
WDiffNodeset数据结构采用加权节点树(WN-tree)[18]节点编码模型,给定WD并设置一个minws后创建加权节点树,然后生成加权频繁1-项集L1和一个WN-tree。假设WD如表1所示(随机设minws=0.5),所构建的WN-tree如图1所示。创建WN-tree的算法(constructing_WN_tree)参考文献[18]。

表1 样本加权数据库WD

图1 WN-tree结构
性质1对于WN-tree中的任意2个节点N1和N2(N1≠N2),当且仅当N1.pre-value
1.3 WNodeset和WDiffNodeset
WDiffNodeset是一种基于WNodeset的数据结构。
定义5(加权频繁1-项集的WNodeset) 给定一个WN-tree,对于加权频繁1-项集i,将所有节点名称为i的WN-code[18]组成的集合定义为i的WNodeset。每一个i的节点集都按照WN-code中的pre-value值升序排列,加权频繁1-项集中的WNodeset如下所示:
C→{(1,8,2.4)},E→{(2,6,2)},A→{(3,3,1.4),(9,7,0.4)},D→{(4,1,1),(7,5,0.4)},F→{(5,0,0.5),(6,2,0.4),(8,4,0.4)}
性质2给定一个项集,假设{(x1,y1,z1),(x2,y2,z2),…,(xl,yl,zl)}是相应的WNodeset,则存在x1x2…xl且y1y2…yl。
定义6(加权频繁k-项集的WNodesets) 令P=i1i2…ik-1ik为一个项集(ij∈L1,i1i2…ik),将P=i1i2…ik-1ik的加权节点集表示为WNodesetP,将P1=i1i2…ik-2ik-1的加权节点集表示为WNodesetP1,将P2=i1i2…ik-2ik的加权节点集表示为WNodesetP2,则有WNodesetP=WNodesetP1∩WNodesetP2。
定义7(加权频繁2-项集的WDiffNodesets) 给定2个项集i1、i2(i1、i2∈L1∧i1i2),用WNodeseti1和WNodeseti2分别表示i1和i2的加权节点集。加权2-项集i1i2的WDiffNodesets用WDiffNodesetsi1i2来表示,即:WDiffNodesetsi1i2={(x.pre-value,x.weight)|x∈WNodeseti1∧(∃y∈WNodeseti2,与y对应的节点是与x对应的节点的祖先)}。WDiffNodesetsi1i2中的元素按pre-order的升序排列。例如:A→{(3,3,1.4),(9,7,0.4)},F→{(5,0,0.5),(6,2,0.4),(8,4,0.4)},其中,根据性质2可得(3,3,1.4)是(6,2,0.4)和(5.0.0.5)的祖先而不是(8,4,0.4)的祖先,而(9,7,0.4)不是任何节点的祖先,因此,FA的WDiffNodesets为(8,0.4)。同理,FD的WDiffNodesets为(6,0.4)。
定义8(加权频繁k-项集的WDiffNodesets) 令P=i1i2…ik-1ik是一个项集(满足ij∈L1∧i1i2…ik)。将P1=i1i2…ik-2ik-1的加权节点集表示为WNodesetP1,P2=i1i2…ik-2ik的加权节点集表示为WNodesetP2。则P的WDiffNodesetP计算公式为:
WDiffNodesetP=WDiffNodesetP1/WDiffNodesetP2
(3)
其中,“/”表示集合差。
性质3给定2个项集P1=i1i2…ik-2ik-1、P=i1i2…ik-1ik,将WDiffNodesetP表示为WDNP,则ws(P)的计算公式为:
(4)
证明令P2=i1i2…ik-2ik,将WNSP、WNS1、WNS2表示为P、P1、P2的加权节点集,由定义6、定义8分别得到WNSP=WNS1∩WNS2,WDNP=WNS1/WNS2。
性质4令P=i1i2…ik-1ik是一个项集(满足ij∈L1∧i1i2…ik),将P1=i1i2…ik-2ik-1的WDiffNodeset表示为WDN1,P2=i1i2…ik-2ik的WDiffNodeset表示为WDN2,P的WDiffNodeset表示为WDNP,则WDNP的计算公式为:
WDNP=WDN2/WDN1
(5)
证明令X=i1i2…ik-3ik-2,Y=i1i2…ik-3ik-1,则X、Y、P1、P2的WNodeset分别定义为WNSx、WNSY、WNS1、WNS2。由定义6和定义8分别可得:
WNS1=WNSX∩WNSY
(6)
(7)
由式(6)、式(7)可得:
WNSX=(WNSX∩WNSY)∪(WNSX/WNSY)=
WNS1∪WDN1
WNS1∩WDN1=∅,WNS1=WNSX/WDN1
同理:
WNSX=WNS2∪WDN2,WNS2∩WDN2=∅,
WNS2=WNSX/WNS2
最后结果为:
WDNP=WNS1/WNS2=(WNSX/WDN1)/
(WNSX/WDN2)=WNSX∩(WDN1)T∩
WDN2=WDN2∩(WDN1)T=
WDN2/WDN1
2 DiffNFWI算法
2.1 搜索空间
加权频繁项集挖掘问题可以用一个集合枚举树表示,以数据库WD(表1)为例,其项xi∈I={F,D,A,E,C},且F 图2 集合枚举树 算法1所示为构建2-项集WDN的伪代码。 算法1Build 2-itemset-WDN(ixiy) 1.WDNxy←∅,k←0 and j←0; 2.lx← the length of WNx(WNodeset of ix) and ly←the length of WNy(WNodeset of iy); 4.if WNx[k].post-value>WNy[j].post-value then: 5.j←j+1; 6.Else 7.if WNx[k].post-value 8.k←k+1; 9.Else 10.WDNxy←WDNxy∪{(WNx[k].post-value,WNx[k].weight)}; 11.k←k+1; 12.End if 13.End if 16.WDNxy←WDNxy∪{(WNx[k].post-value,WNx[k].weight)}; 17.k←k+1; 18.End whlie 19.Return WDNxy 构建2-项集WDN时采用混合搜索策略来构建ixiy的WDiffNodeset。比较WNodeset中的2个WN-code,直到其中一个WNodeset的所有元素都比较完毕。可以通过“祖先-后代”的关系来比较2个节点集中的所有元素以创建WDiffNodeset,但是该操作效率很低,复杂度为O(x·y)。根据性质2和性质4,本文提出算法1,并根据如下3种情况来减少2个元素之间的比较次数,此时时间复杂度为O(x+y)。 情况1若WNx[k].post-value>WNy[j].post-value,此时,与WNy[j]对应的节点不是与WNx[k]对应的节点的祖先。由性质2可得,各项集WNodeset均是按照post-value升序排列,因此,WNy[j]不符合要求,继续选取WNy[j+1]与WNx[k]进行对比。 情况2若WNx[k].post-value 情况3若WNx[k].post-value DiffNFWI算法采用NFWI算法的剪枝策略来修剪搜索空间。 性质5(剪枝策略[18]) 给定项目集P、Q和一个项目i,满足P∩Q=∅,i∈P且i∈Q,如果ws(P)=ws(P∪{i}),则有: ws(P∪Q)=ws(P∪Q∪{i}) (8) 例如在表1中,令P=F,i=E,Q=C,ws(F)=ws(FE)=1.3,因此,ws(FC)=ws(FEC)=1.3。证明过程参考文献[18]。 DiffNFWI算法以事务数据库、一个minws作为输入,算法2所示为DiffNFWI的伪代码。首先进行初始化,DiffNFWI框架由3个部分组成:第一阶段,扫描WD,删除小于minws的项,对每一个事务里的项排序,从而创建WN-tree树;第二阶段,遍历WN-tree确定所有的频繁1-项集及其WNodesets,构造所有层次为1的集合枚举树(即加权频繁项集树);第三阶段,确定所有的加权k-项集及其WDiffNodesets(k≥2),构造层次为k的集合枚举树。其中,第三阶段细分为确定加权频繁2-项集和加权频繁3-项集。DiffNFWI算法采用性质5作为剪枝策略,将满足剪枝策略的项集放入等价项集中,最后输出集合枚举树和等价项集中的所有结果。 算法2DiffNFWI算法 输入WD,minws 输出加权频繁项集F //第1步创建WN-tree 1.F=∅;//初始化F为空集 2.调用constructing_WN_tree(WD,minws) 3.F=F∪L1;//L1为有序的频繁1-项集 //第2步遍历WN-tree,确定频繁1-项集 4.Scan WN-tree to find WNodesets//找到WNodesets 5.Create the node childi with level 1;//构造层次为1的//集合枚举树 //第3步确定所有的频繁k-项集(k≥2) 6. For each 2-itemsets ixiydo//频繁2-项集循环 7.call Build 2-itemset-WDN(ixiy);//调用算法1产生//WDiffNodeset; 9.if ixiy.wsminws*|WD|,then 10.F2=F2∪{ixiy}; 11.Create the node childi with level 2;//构造层次为2的//集合枚举树 12.End For 13.For each weighted frequent itemsets do//频繁k-项集 14.call constructing_frequent_ itemset_tree; 15.End For 16.Return F//输出集合枚举树与等价项集中的所有集合 算法2在挖掘加权频繁k-项集时调用了算法3的函数,然后采用性质3计算加权支持度计数,再利用性质5修剪搜索空间,将满足条件的项放入等价项集中,若不满足剪枝策略再判断是否满足minws,接着对满足条件的节点创建集合枚举树。算法3第7行描述了剪枝策略,其中,N表示当前节点,将满足条件的项保存在等价项集中,该项无需构建当前节点的子节点,原因是与这些项集相关的加权频繁项集的所有信息都保存在当前节点中,从而大幅降低了搜索空间。 算法3constructing_frequent_itemset_tree算法 1.For each k-itemset WDiffNodeset(P) do: 2.X=WNd.itemset;//X=i1i2…ik-1 3.Y=(X-X.last_item)∪{i};//X-X.last_item是从X//中删除的最后一项子集,即Y= i1i2…ik-2 4.P=X∪{i};//P= i1i2…ik-2ik 5.P.WDN=X.WDN/Y.WDN;//利用性质4构造WDN 7.if P.ws=X.ws then://剪枝策略 8.N.equivalent_items=N.N.equivalent_items∪{i}; //将满足剪枝策略的项集放入等价项集中 9.Else if P.ws≥|WD|×minws then//判断阈值 10.Create the node childi with leve k; 11.End if 12.End if 13.F为集合枚举树与等价项集的并集 14.End For NFWI算法采用WN-List数据结构,而本文DiffNFWI算法采用WDiffNodeset数据结构。WN-List和WDiffNodeset都是基于WN-tree来存储加权频繁项集的信息。DiffNFWI算法采用了集合枚举树和混合搜索策略相结合的方法来查找加权频繁项集,其中,有3条搜索原则,而NFWI算法仅采用性质2作为搜索原则。因此,DiffNFWI算法可以实现高效的查找。其次,DiffNFWI采用性质3高效地计算加权支持度,再结合NFWI算法中的剪枝策略,从而取得了良好的效果。 DiffNFWI算法各阶段复杂度分析如下: 1)第一阶段:DiffNFWI算法调用constructing_WN_tree(WD,minws)算法中的constructing_WN_tree函数。首先扫描WD,移除不满足minws的项目,并将每一个事务中剩余的项进行排序,最坏情况下的复杂度为O(m·lt);然后DiffNFWI根据排序后的WD创建WN-tree,最坏情况下的复杂度为O(lt·logalk)。因此,算法第一阶段的复杂度为O(m·lt·logalt·lt)。其中,m为WD中的项目数量,lk为WD中的事务最大长度。 2)第二阶段:算法产生频繁1-项集的过程。DiffNFWI遍历WN-tree并且产生WNodesets的加权频繁1-项集,因此,该阶段的复杂度为O(m·lt),在最坏情况下,m·lt是树的大小。 3)第三阶段:算法产生频繁k-项集的过程(k≥2)。该算法采用集合枚举树与混合搜索策略相结合的方法查找加权频繁项集。算法1中的混合搜索策略的时间复杂度为O(x+y),其中,x和y分别对应2个节点集的长度。集合枚举树的节点数为2n-1(n为加权频繁1-项集的数量),最坏情况下NFWI算法执行WDiffNodeset交集运算后,创建了集合枚举树的所有节点(没有剪枝),因此,该阶段的复杂度为O(2n·(x+y))。 综合上述分析,DiffNFWI算法的时间复杂度为O(m·lt·logalt·lt+m·lt+2n·(x+y)),由于m·lt·logalt·lt+m·lt远小于2n·(x+y),因此DiffNFWI算法的时间复杂度为O(2n·(x+y))。 影响NFWI、DiffNFWI算法运行时间的是系数(x+y)。在NFWI算法中,x和y分别为2个WN-List的长度,在DiffNFWI算法中,x和y分别为2个WDiffNodeset的长度,WDiffNodeset表示差异节点集,是不包含频繁k-项集的集合,而WN-List是包含该项目的集合。在密集数据集中,DiffNFFWI算法的(x+y)系数相对于NFWI算法较小,因此,DiffNFWI算法在密集数据集中性能明显优于NFWI算法。 本文进行3组仿真实验来对比NFWI和DiffNFWI算法的有效性和可行性。实验环境如下:操作系统Window7(64位),开发工具Visual Studio C++2010,语言为C/C++,8 GB内存容量,英特尔i5处理器。 本文选取mushroom、pumsb、T40110D100K和T1014D100K数据集进行评估实验,这4个数据集均下载自SPMF[21]文库。在4个数据集中,项的权重在1~10整数之间随机产生(可参考文献[18]),然后通过改变最小加权支持度阈值来进行加权频繁项集挖掘,最后对比分析2种算法在不同数据集中的时间消耗情况。表2所示为数据集特征。 表2 数据集特征信息 3.2.1 运行时间比较 在每组实验中2种算法所挖掘到的加权频繁项集均相同,图3所示为不同minws下2种算法的运行时间对比。从图3可以看出,在mushroom、pumsb、T40110D100K、T1014D100K数据集中,当minws分别为2%、65%、0.4%、0.02%时,与NFWI算法相比,DiffNFWI算法的运行效率分别提高64.2%、67.9%、48.4%和27.0%,minws越小,DiffNFWI算法性能优势越明显,随着minws的升高,DiffNFWI算法的优势逐渐下降,即本文DiffNFWI算法性能优于NFWI算法,尤其在密集数据集中,算法优势更明显。 图3 2种算法运行时间对比 3.2.2 内存比较 图4所示为DiffNFWI和NFWI在挖掘时的内存消耗情况,从图4可以看出,随着阈值的不断减小,与NFWI算法相比,DiffNFWI算法在4种不同数据集中的内存没有明显的变化,且其内存小于NFWI算法。 图4 2种算法内存大小对比 本文提出一种DiffNFWI算法,以解决NFWI算法在数据集中因大量交集计算导致效率低的问题。DiffNFWI算法在DiffNodeset结构的基础上加入权值得到WDiffNodeset结构,利用该结构挖掘加权频繁项集,从而降低算法的运行时间。实验结果表明,相比NFWI算法,DiffNFWI算法的运行效率较高。下一步将采用基于集合位图表示的前缀编码模型来提高算法性能,并针对加权最大频繁项集挖掘、闭频繁项集挖掘以及top-k频繁项集挖掘等任务进行深入研究。
2.2 主要剪枝性质
2.3 DiffNFWI算法描述
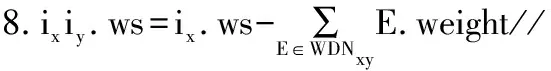
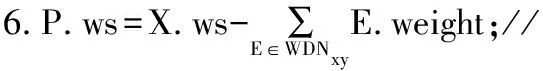
2.4 NFWI算法和DiffNFWI算法的对比
2.5 DiffNFWI算法复杂度分析
3 实验验证
3.1 数据集介绍

3.2 结果分析


4 结束语

