有监督时间序列分割与状态识别算法

史明阳,王 鹏,汪 卫

(复旦大学 软件学院,上海 201203)

0 概述

时间序列分割是获取时间序列内在信息的重要方式,在数据挖掘领域备受关注。当前的时间序列分割算法多为无监督类型,相同的时间序列可以具有多种不同可解释的分割模式。在实际情况中,每一个片段的监控数据通常对应于被监控对象不同的实际物理状态。显然,在通过不同分割方法获得的大量分割结果中,并不是每一种分割模式都符合用户的期望。因此,能够选择分割的模式在整个识别过程中就显得尤为重要。

目前关于时间序列分割方式及其状态判断的研究较少,在此背景下,本文提出一种有监督的时间序列分割与状态识别算法SSR。通过构建特征高斯概率分布模型设计相关序列的特征,在此基础上,利用匹配损失计算和改进的贪心策略设定特征权重约束,并利用增加分割位置约束条件及增量计算2种优化方式进一步提高算法效率。

1 相关工作

关于时间序列分割及状态识别问题的解决方法,目前研究成果较多。文献[1]提出一种基于重要点的时间序列分割方法,将考察时间窗扩展到前一重要点、待考查点和下一指定时间窗之间,再通过考察时间窗口内待考察点两边模式和变化幅度来确定重要点,从而减小分割误差。文献[2]提出一种基于重要点与灰色GM(1,1)模型的时间序列分段算法,在保留全局特征的同时保持局部性质,能够以较小的拟合误差实现序列的压缩。文献[3]提出基于信息颗粒和模糊聚类的时间序列分割方法,使得时间序列的分割具有数据上的同质性,得到既有时间信息又具有同质性的时间序列分割结果。文献[4]则提出一种基于Floyd算法的海温时间序列分割方法。

隐马尔科夫模型(Hidden Markov Model,HMM)是时间序列分割算法中一种常用的典型模型,其中SWAB[5]和pHMM[6]能够从时间序列中进行线性分割。pHMM是基于模式的隐马尔科夫模型[7]和SWAB的改进,旨在揭示生成时间序列数据的系统全局图。AutoPlait[8]是另一种典型的时间序列分割算法,它使用最小描述长度(MDL)和多级链模型(MLCM)对时间序列的替代HMM评分从而进行分割。FLOSS[9]是一种基于Matrix Profile[10]构建的在线流媒体语义分割方法。

现有的时间序列状态识别方法可分为两大类[11],一类是基于形状的方法,其通过相似性度量来测量原始数字数据中时间序列之间的距离,此类方法可以实现高精度,但计算昂贵,基于欧氏距离[12]或DTW距离[13]构建的传统1NN分类器为其典型示例;另一类是基于结构的方法,其使用一些方法来描述类的特征,此类方法更能有效地抵抗噪声,如SAX-VFSEQL[14]和SAX-VSM[15]在SAX[16]表示时间序列上构建分类器。

2 问题描述

为阐述方便,首先给出本文研究的相关概念和问题的基本定义。

2.1 相关定义

定义1(时间序列) 一条时间序列T={t1,t2,…,tn}是长度为n的相等间隔实际值的连续有序序列。

定义2(子序列) 一条时间序列T的子序列s是T的子集,其中s的长度小于或等于T。

通常,时间序列数据是从真实的物理环境中获得的,这意味着其中包含真实的物理意义。根据用户需求和序列的实际情况将时间序列分割为子序列,对于分割结果中分割的子序列和相应的语义描述,称为片段和状态。

定义3(片段) 一个时间序列T的第i个分割片段SEGi,是时间序列T分割后的第i个子序列。所以,时间序列T可以用分割片段表示为T={SEG1,SEG2,…,SEGm},其中m为此分割模式中子序列的数量。

定义4(状态)子序列SEGi的状态ci是指SEGi所属的分类表示。

本文研究目标是将一条完整时间序列分成多个片段并对每一个子序列片段进行状态识别。根据上文子序列和状态的定义,一个时间序列的分割模式可以定义如下:

定义5(分割模式) 一个关于时间序列T的分割模式可以表示为S(T)={,,…,},其中,m为这个分割模式中片段的数量,ri表示第i个片段的分割点位置,ci表示第i个片段的状态类别。分割模式S(T)的第i个分割片段可以表示为SEGi={tri-1+1,tri-1+2,…,tri}。

SSR针对状态类别已知的时间序列数据,使用有监督的方法建立分类模型。所需要的训练集为带有状态标记的子序列集合。

2.2 问题定义

根据上文描述,本文目标为寻找时间序列的一个分割模式,并根据已知限定信息找到每个段的状态,使得这个分割模式能够最大程度符合用户的期望。此处给出一个形式化的问题定义如下:

定义7给定带有状态类别标记的训练数据集TS和待分割时间序列T={t1,t2,…,tn},寻找T的最优分割模式S*(T)={,,…,}使匹配损失最小。匹配损失的计算将在3.3节给出。

3 时间序列分割与状态识别算法SSR

SSR基于特征高斯概率分布模型及概率最大化思想进行时间序列状态识别,基于调整后的贪心策略进行时间序列分割,其中时间序列状态识别主要分为2个过程,即建立特征高斯概率分布模型和计算匹配损失。

3.1 特征高斯概率分布模型

带有良好标记的训练集可以提供有价值的指导作用,基于有监督的方法可以获得更符合用户期望的分割模式,而能够从训练数据集中提取相关信息并合理利用是整个过程中的关键一步。本文通过对训练集中同一类别的样本数据提取相应特征,构建特征高斯概率分布模型。

3.1.1 特征选择

首先应合理选择需要从训练集中提取的特征,从而更准确地描绘不同的序列。在综合考虑各种特征指标之后,选定以下6个特征作为衡量标准,分别是样本序列的长度、均值、标准差、过零率、拟合斜率以及根据拟合斜率所产生的均方误差(Mean Squared Error,MSE)损失。

通过不同状态类别样本序列的平均值,结合序列的长度、标准偏差和过零率,可以得到该类别序列的近似振动程度。同时,通过斜率和MSE损失能够对时间序列的趋势进行大致判断。通过上述6个特征,可以粗略描绘出不同状态类别时间序列对应的特点。

3.1.2 特征高斯概率分布模型

特征模型是根据不同的状态类别建立的。在训练数据集中,每一个特征类别下都有多个样本序列数据。在确定提取特征以后,对每一个状态类别中样本序列的每一个特征进行计算,同时记录该特征值数值的均值和方差,以建立一个特征高斯概率分布模型,表示为M和Σ。Mi,j和Σi,j分别表示状态类别i中的样本序列集关于第j个特征值的均值和方差,计算公式为:

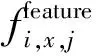
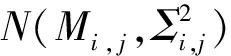
3.2 特征的权重约束设定

上文给出了特征选择及特征高斯概率分布模型的建立过程。但是在真实场景的数据中时间序列的形态多样,其特点属性各异,在全部6个特征中,对于不同的时间序列,不同的特征对于状态类别的区分度是不同的。所以,对于特征设定不同的权重约束是必要的。本文通过引入置信度分数来设定特征的权重约束,通过在训练阶段评估每个指标的分类性能来学习置信度分数。

在训练阶段,分别使用单一的特征进行类别区分,计算针对当前类型时间序列数据当前特征的分类准确度,再对6个对应的准确度分数进行归一化处理,得到调整后的置信度分数w1,w2,…,w6作为每个特征的权重。

3.3 匹配概率及损失

(1)

通过上述计算,可以得到对于一个T的分割模式S(T)={,,…,}(下文简写为S)的匹配概率为:

(2)

其中,fSEGi,j表示SEGi第j个特征值。

在实际计算过程中,程序处理精度也是需要考虑的问题,由于1以内浮点数的运算会引入较大的误差,因此需要对计算过程做进一步处理。在整体寻找最佳匹配状态类别的过程中,关注的并不是概率的绝对数值,而是概率之间的相对关系,可以对匹配概率做如下处理:

对式(2)进行代数变换,得到:

(3)

定义匹配损失为:

(4)

将上文给出的权重约束引入损失计算,改写式(4),可得到分割模式S的匹配损失为:

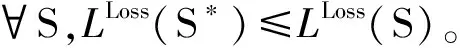
3.4 片段分割算法

SSR基于贪心的思想,通过迭代的方式进行时间序列的分割。

设对于时间序列T,当前已进行i-1轮分割过程,第i-1个分割片段的分割点为ri-1,第i轮的分割过程如下:

对于每一类别由下式进行匹配损失计算,得到ci,使得:

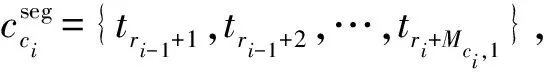
在确定当前分割片段的状态ci以后,根据前一分割点ri-1、状态ci长度特征的均值Mci,1和标准差Σci,1,对分割点ri的范围进行限定,得到:

ri-1+Mci,1-3×Σc1,1≤ri≤ri-1+Mci,1+3×Σc1,1

最后,在限定范围内逐点扫描,得到匹配损失最小的点ri作为具体分割点,使得:

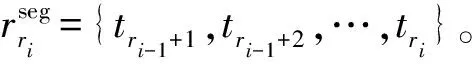
至此,得到及第i个分割片段SEGi。

为避免单一类别匹配所产生的局部偏差造成全局的负面影响,本文对SSR的分割过程进行调整。在状态类别匹配损失计算的过程中,不仅考虑当前分割片段SEGi的状态类别,同时考虑下一序列片段SEGi+1的状态类别,从而减小当前序列片段的影响程度。

在确定类别的过程中,每次使用2个状态类别进行匹配损失计算,得到ci、ci+1,使得下式成立:

这种调整可减少当前片段的影响程度,从而减小局部偏差对全局的影响。

4 算法效率优化

为提升SSR的算法效率,本文提出了2种算法效率优化方式,即通过增加分割点的约束条件及采用增量计算的方式进行特征提取。

4.1 分割点约束条件

在上文介绍的算法过程中,对于分割片段SEGi具体分割点位置ri的选定,采用的是扫描并计算匹配损失的方式。显然,在不靠近真实分割边界的部分,相邻点之间的匹配损失差值极小,逐点计算匹配损失会产生大量冗余的计算过程。

时间序列中状态发生变化的位置,通常伴随一个或多个特征大幅变化,称时间序列中发生这样巨大变化的点为特殊点。特殊点通常在时间序列上显示为不一样的形状,例如拐点、峰值点等,而实际的分割点也更可能在这些特殊点中产生。因此,在算法过程开始之前首先预处理可能的候选分割点集,并在寻找具体分割点的过程中只扫描候选区间内的候选点,从中确定具体分割位置。具体求取方法为:以设定滑动窗口的方法求取窗口内各特征值的极值点,在对原始序列数值及每一个特征单独判断后,得到特殊点集合,即分割点候选集A。

那么,对于时间序列T的第i个分割片段SEGi,其状态分类为ci,在寻找具体分割点ri时,约束条件为:1)ri∈[lci-3×dci,lci+3×dci];2)ri∈A。

这样的处理方式,实际上是对扫描及对应的损失计算过程进行剪枝操作,从而在不影响精度的情况下降低运算量。

4.2 增量计算优化

在算法计算过程中,需要根据当前分割点截取序列并从子序列中提取特征,而如果每次均重新计算特征,显然会带来大量重复的计算。笔者通过分析选定的6个特征指标发现,平均值、标准偏差、斜率及过零率4个指标都可以通过预处理增量序列的方式减少冗余的计算过程。

在开始分割过程之前,计算待分割时间序列T的前缀和序列、平方前缀和序列及过零次数和序列。这样在每次提取特征的过程中,不需要重复累加的过程,从而节省了大量的时间。同时采用文献[17]的方法,将时间序列片段的拟合斜率及截距改写为:

(5)

(6)

同理,在式(5)及式(6)中也可以使用前缀和序列进行增量计算,从而减少计算量。限于篇幅,此处不作展开说明。

4.3 时间复杂度估算

基于SSR的算法原理及2种优化方式,在整个分割及识别过程中,将大量的计算复杂度转移到训练阶段,使预测阶段的复杂度大幅减小。

由于整个时间序列分割及状态识别过程的计算复杂度受分段模式选择的影响较大,因此本文基于分段数量及子序列长度对预测过程进行计算复杂度的估算。

然而在实际情况中分割模式多样,片段数量及片段长度都存在不同且差异巨大,并不能简单地根据平均长度进行估算,且各特征特殊点常有重合或近似,也并不会对所有分割点都进行匹配。此处给出的复杂度仅为平均情况下的粗略估算值。

5 实验及结果分析

针对本文算法SSR,在真实场景的数据集上进行多角度的实验验证。实验主要从状态识别的准确度、用户意图的匹配程度进行分析,并进一步对算法加以扩展,验证其在多维数据上的效果,同时对优化方法的效果进行对比实验。

5.1 实验环境

实验平台基于Windows 10,64位操作系统,Intel®Core(TM) i7-7700K处理器,4.20 GHz主频,带有16 GB内存的台式计算机。SSR算法使用Python语言实现。

5.2 数据集

本文实验在以下3个真实场景的数据集上进行:

1)PAMAP行人运动数据集,下文简称运动数据集。PAMAP是一种有氧运动数据监测方案,用于记录老年人身体的监测数据。此数据监测系统监测受试者的全球活动,识别基本的有氧活动并估计其强度水平[18-19]。整个数据集包含6个被试,每个科目有40多个维度的数据,主要包括4种类型的监测传感器数据,即心率、IMU手部监测、IMU胸部监测和IMU足部监测数据,其中共7种运动状态:步行非常慢,正常步行,越野行走,跑步,骑自行车,跳绳和踢足球,其中每个时间序列长度约180 000。

2)卫星桌面联试试验数据集,下文简称卫星数据集。此数据集源自于真实的卫星桌面在线试验,记录了卫星运行的指标。实验主要关注电池电压和姿态控制的变化。电池电压序列包括3种不同的充电和放电过程,姿态控制包括2种不同的运动状态,其中所有序列的长度均为207 908。

3)地铁运行工况监测数据集,下文简称地铁数据集。此数据集记录了真实的地铁运行的监测数据,通过安装在内部托架上的传感器监测地铁运行过程。本文实验主要关注速度和角速度序列。此数据集包括加速、减速、匀速和转弯4种运行状态,其中每个时间序列数据的长度均为94 221。

真实场景的数据对应于现实世界物理对象的活动。对于所有实验,本文将数据集中约70%的数据设置为训练集,其余作为测试集。

5.3 序列分割与状态识别实验

时间序列的分割及状态识别是时间序列分析的经典主题。本文实验中选用pHMM[6]和AutoPlait[8]作为对比算法。AutoPlait是一个无参数算法,pHMM由seg_error和rel_error 2个参数控制,实验中将调整pHMM的参数以获得更好的结果。

图1和图2展示了卫星数据集和地铁数据集的实验结果,每组结果的第一张图为原始标签的分割及状态展示,后三组结果分别为SSR、AutoPlait和pHMM的实验结果。由于pHMM运算规模的限制,在运动数据集上仅能使用1/4长度的序列进行实验。图1(d)中seg_error和rel_error分别为0.1和4.0,图2(d)中则分别为0.1和0.8。

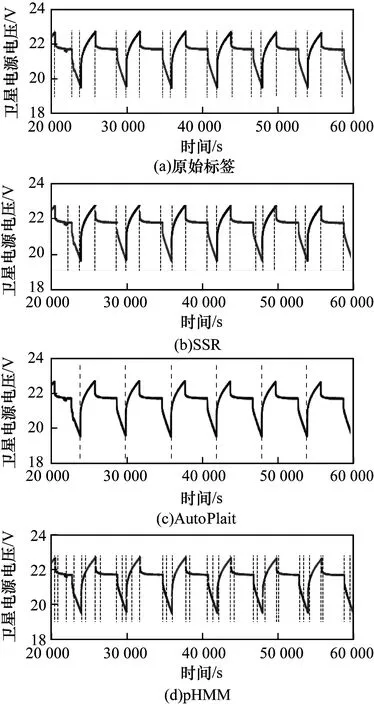
图1 在卫星数据集上的实验结果1

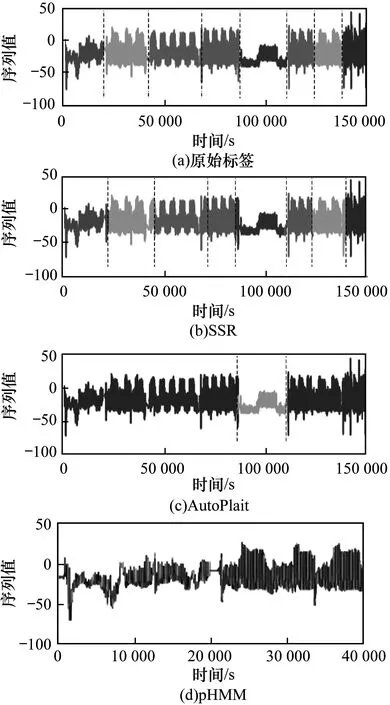
图2 在地铁数据集上的实验结果1

在两组实验下,SSR都显示了其优越性。pHMM使用长度和斜率来描述序列,AutoPlait通过平均值和方差来区分序列类别。SSR采用了6种特征对序列进行描绘,可以全面地表达状态类别,展现了其在状态类别区分的明显优势。从特征选择上,AutoPlait很难对具有稳定均值和方差的序列进行分割。因此,AutoPlait在这类序列中效果并不理想。pHMM展现了对状态的识别优势。在卫星数据集上,pHMM所得到的状态结果区分明显,但是难以与实际电池充放电过程相关联;而在运动数据集上,pHMM得到分类结果非常杂乱。这两种算法的分割和状态识别结果均不理想。SSR在这两组实验中都有着比较好的表现,可以很明显地区分卫星数据的充放电过程及不同的运动状态。这是因为使用了6个特征识别状态类别,可以对序列进行更精细的描绘。在SSR的分割结果中,分割点仍然存在一定的偏差。这样的误差产生主要是由于被试者之间的个体差异非常大,例如被试的年龄、性别、身高和体重。相对于整个序列的长度和状态类别的多样性,这样的误差是可接受的。

此外,pHMM和AutoPlait均只能获得单一的分割模式。经过参数调整后,pHMM的结果显示了一定的周期性。然而,pHMM结果的周期性显然不符合通常理解下对于周期性的要求。而SSR可以根据用户意图实现不同的分割模式。通过对比实验结果可知,相比pHMM和AutoPlait,SSR在时间序列状态识别和分割中性能更好。

表1中给出了本文算法在3种数据集上的实验结果准确度,其中状态分类准确率表示正确识别状态的序列片段比例,最大分割点误差表示在正确状态识别的分割片段中的最大的误差值占序列总长度的比例。所有的实验均得到与用户的意图一致的分割模式。

表1 实验结果准确度统计

5.4 用户意图理解实验

获得与用户意图一致的分割模式是SSR主要期望实现的目标,用户意图理解实验在卫星数据集上进行。

对于卫星数据集,主要关注每个指标的电压和位置数据的状态变化。通过图3(a)上的标注,可以看到3个非常明显的状态变化点,图3(b)中则显示了一个卫星电源电池电压变化过程中充电和放电3个阶段:充电过程,缓慢放电过程及迅速放电过程。

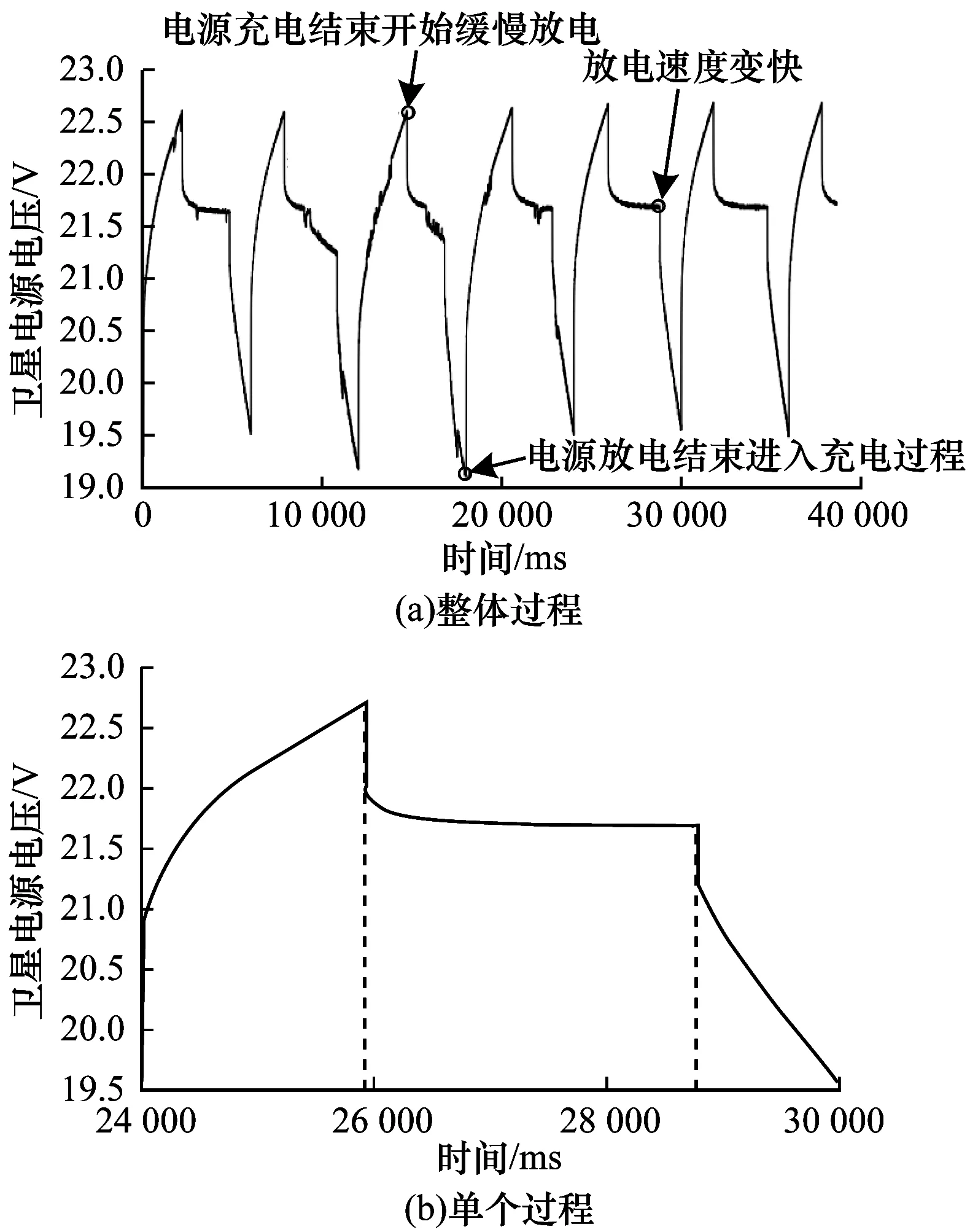
图3 卫星电源电池数据形态示意图

实验针对整个过程设计了2种分割模式的训练集:考虑单个充放电为一个状态类别(模式1)以及考虑一个完整充放电周期为一个状态类别(模式2)。同样的模式分割方法也适用于姿态控制序列。图4和图5分别展示了本文算法针对2种分割模式的结果。其中,图4为电池电压序列上的实验结果,图5为姿态控制序列上的实验结果。可以明显看出,SSR可以根据用户设定进行序列的分割及状态识别,并得到2种不同分割模式的结果,而且分割位置的结果也比较准确。由此可知,SSR可以很好地理解用户的意图并获得相应的分割模式。

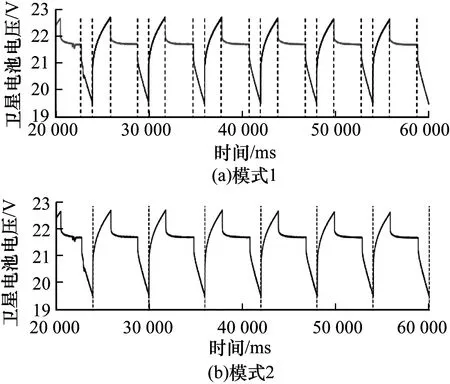
图4 在卫星数据集上的实验结果2

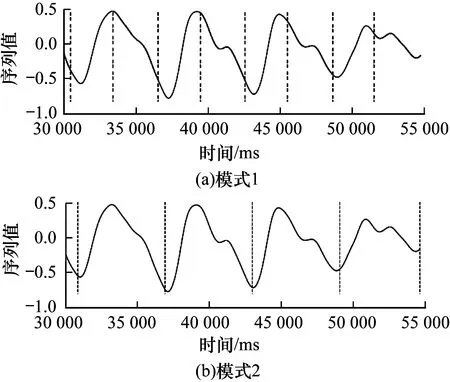
图5 在卫星数据集上的实验结果3

5.5 多维扩展实验

在本文研究中,期望算法能够具有更好的扩展性。多维扩展实验在地铁运行监测数据集上进行,实验结果如图6所示。

图6 在地铁数据集上的实验结果2

从图6可以看出,在速度序列中,SSR算法可以区分4种运行状态,即加速、减速、匀速与转弯;在角速度序列中,只关心是否处于转弯状态。可以看出,在角速度序列上,几乎所有转弯与非转弯状态都可以很好地区分。对于速度序列,在加速与减速过程中,斜率特征可以起到良好的区分作用。而针对于匀速与转弯的状态,在角速度序列上的均值特征有着明显的不同,从而可对不同的状态加以区分。

5.6 优化验证实验

优化验证实验在运动数据集上进行。在优化实验中,对比了基础版本的算法(basic-SSR)、增加了增量计算的基础算法(incre-SSR)以及添加全部优化的最终算法(SSR)的效率。3个版本的算法在分割准确度上没有明显的区别。运行时间对比结果如图7所示,可以看出,增加了优化策略以后,在实验结果准确度几乎没有改变的情况下,时间效率获得了大幅的提高。

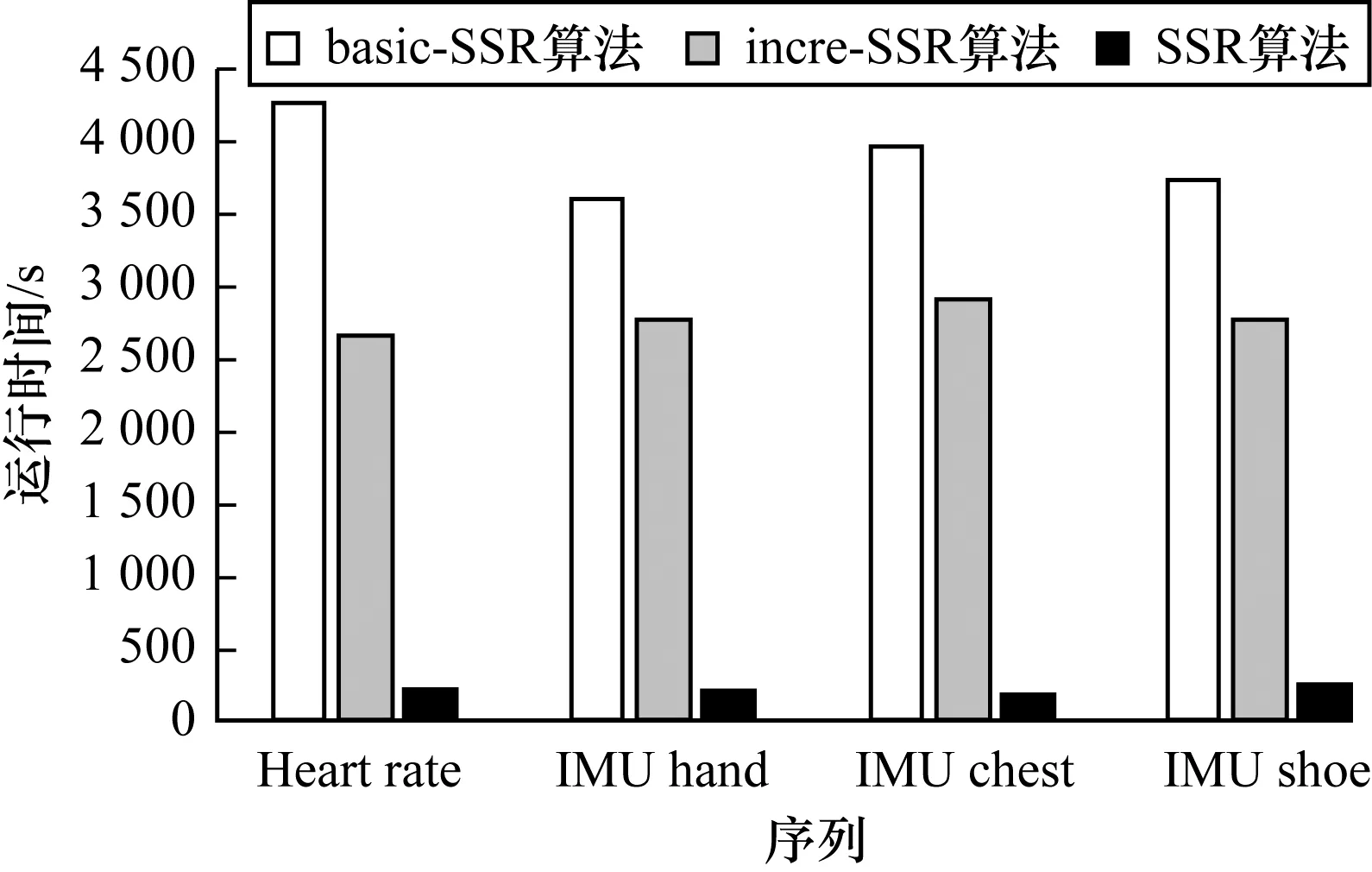
图7 算法优化前后的运行时间比较

6 结束语

针对同一时间序列有多种可解释分割模式的情况,本文提出一种有监督的时间序列状态识别方法,以期获得与用户意图一致的时间序列分割结果。通过建立特征高斯概率分布模型,设定特征的权重约束,利用概率最大化的思想判断状态类判别,基于调整后的贪心策略的进行序列分割,同时设计算法的效率优化策略与多维扩展方式。在真实场景数据集上的实验结果验证了本文研究的有效性与可扩展性。为进一步提高算法的可扩展性,后续将扩展有关优化策略,并基于Apache Spark[20]等分布式计算平台实现本文算法及相应的优化剪枝策略,以应对分布式情景下更大数据规模和更高效率要求所带来的技术挑战。