一种分类型矩阵数据的初始聚类中心选择算法

田 璐,曹付元,余丽琴

(1.山西大学 计算机与信息技术学院,太原 030006; 2.计算智能与中文信息处理教育部重点实验室,太原 030006)

0 概述

在数据挖掘中,多数算法的输入是由n个对象组成的一个集合,每一个对象对应一条记录且被多个属性所描述[1]。然而在实际应用中,一个对象的描述常常不止一条记录,通常由多条记录描述的对象称为矩阵型对象,由矩阵型对象构成的数据集称为矩阵数据集,即由包含多条记录的对象组成的数据集。例如,在超市购物时,每个用户购买的商品不仅种类不同,而且在购买同一种商品时,购买的商品数量和频率也不相同。通常,可以根据人们购买一个商品的数量和频率来预测该用户是否喜欢这个商品。因此,矩阵数据蕴含了丰富的用户行为特性,对于行为分析具有重要的价值[2]。

在实际生活中,矩阵数据广泛存在于通信、超市、银行、保险以及各大电子商务应用领域。为了给用户提供更好的服务,需要挖掘这种数据中潜在的有用信息并加以利用。然而,在实际应用中大部分矩阵型数据没有标记,如果给全部数据进行标记,需要耗费大量的人力物力,代价昂贵。通过无监督学习来对这类型数据进行分析是一种最直观的方法,其中聚类是无监督学习中一种最广泛的应用。文献[3]提出了k-mw-modes聚类算法来处理分类型矩阵数据,该算法定义了一个新的相似性度量公式来计算两个分类型矩阵对象之间的距离,并且给出了一种新的启发式方法去选择类中心。但是该算法是在随机选取初始类中心之后,通过不断地迭代更新聚类中心实现数据的划分,容易受到不同初始类中心对聚类结果的影响。为了找到一个更好的解决方案,该类型算法需要多次使用不同的初始类中心来重新运行。此外,随机初始化类中心的方法只有在类的个数较少且至少有一个随机初始化结果接近于一个好的解决方案时才有效。因此,初始类中心的选择对划分聚类算法是非常重要的,有必要发展一种面向分类型矩阵数据的初始类中心选择算法以获得更好的聚类效果。

针对分类型矩阵数据,本文根据属性值的频率定义了矩阵对象的密度和矩阵对象间的距离,扩展了最大最小距离算法,在此基础上,提出一种面向分类型矩阵数据的初始类中心选择算法(An Initial Cluster Center Selection Algorithm for Categorical Matrix Data,IC2SACMD)。

1 相关工作

聚类是数据挖掘中一个非常重要的研究方向,也是无监督学习中使用最广泛的一种方法[4]。聚类算法是基于数据的内部结构来寻找观察样本的自然集群。在实际应用中,聚类算法也是一种寻找不同用户群最普遍的方法,使用案例主要包括细分客户、新闻聚类、异常点检测[5]和网络识别等。在k-type聚类算法中,初始类中心的选择至关重要。根据数据类型的不同,初始类中心的选择算法可分为数值型数据和分类型数据初始类中心选择算法。针对数值型数据,研究人员提出几种解决初始化类中心问题的方法[6-8]。相应地,针对分类型数据,研究人员提出了多种解决初始类中心的方法[9-11]。最常见的方法是从数据集中选择前k个不同的对象作为初始类中心。为了避免随机选择初始类中心对聚类结果的影响,文献[9]将由每个属性下频率最高的属性值组成的向量作为初始类中心。虽然文献[9]提出的方法使初始中心多样化,但是对于初始k个中心的选择还没有给出统一的准则。文献[10]提出一种基于密度和距离的方法,通过计算对象自身的密度及对象间的距离来选取初始类中心。虽然该方法一定程度上避免了离群点、初始类中心过于密集的问题,但是在计算密度的过程中没有考虑到不同属性之间的差异、数据对象作为聚类中心的准确性以及第一个类中心的选取可能为全部数据集正中间的一个数据对象。文献[11]提出了一种新的初始化类中心的方法,虽然考虑到数据对象作为类中心聚类的不精准性,并且避免了第一个类中心可能位于全部数据集正中间的一个密度最大值点的情况,但是在计算密度过程中,采用对象间的平均距离作为相似度,该算法也没有考虑到不同属性间的差异性。以上初始类中心算法都应用于每个对象仅由一个特征向量描述的数据集,目前笔者尚未发现针对分类型矩阵数据在选择初始类中心方面的相关工作。

2 k-mw-modes算法

k-mw-modes算法是面向分类型矩阵数据的k-type聚类算法,主要由3个部分组成:1)聚类中心的表示;2)将对象分配到聚类中;3)更新聚类中心。该算法定义了两个矩阵对象之间的距离公式,给出一种更新类中心的方法。

2.1 矩阵对象间的距离

给定两个矩阵对象Xi和Xj,每个对象由m个分类型属性{A1,A2,…,Am}来描述,则Xi和Xj的距离公式定义为:

(1)

其中:

(2)

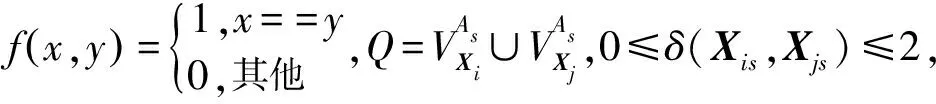
2.2 多加权模式聚类中心

(3)

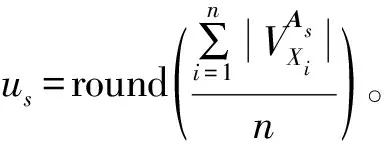
k-mw-modes算法对分类型矩阵数据进行了聚类,但是该算法随机选取初始类中心,没有考虑到随机初始类中心的不稳定性以及必须至少存在一种较优的初始类中心选择才会得到有效的聚类结果。

3 初始类中心选择算法

目前许多专家学者提出了多种方法来度量数据对象间的内聚性[10-12]。最常见的一种方法是使用数据对象与全部数据对象之间的平均距离来测量数据对象的密度[12],因为其简单且没有参数。而对于矩阵数据集,对象Xi对应ri条记录,并且每个对象在每条属性上有多个属性值,即vips表示对象Xi在As属性上的第p个属性值,则需要考虑到同一属性上不同记录之间的差异性。因此,本文根据属性值的频率来定义对象的平均密度。

3.1 基本定义

(4)

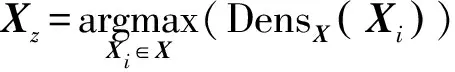
为便于理解,下文给出一个计算矩阵对象的平均密度示例,如表1所示。

表1 矩阵对象的平均密度

根据式(3)计算出在每个属性上各个记录值的权重。

在A1属性上:

在A2属性上:

在A3属性上:

根据式(4)计算每个对象的平均密度如下:

DensX(X1)=w(42)+w(-198)+w(-191)+

w(-109)+w(-142)+

w(-110)=2.333 3

DensX(X2)=w(42)+w(-198)+w(-191)+

w(-190)+w(-199)+

w(-142)+w(-102)=2.000 0

DensX(X3)=w(40)+w(42)+w(-191)+

w(-173)+w(-159)+

w(-142)+w(-63)=1.333 5

可得出对象X1的平均密度最大。

定义2给定数据对象Xi∈X(Xi≠Xz),Xi作为类中心的代表能力定义为:

Pro_Repre(Xi)=DensX(Xi)×d(Xi,Xz)

(5)

图1中的数据集被分为两类,Xz为密度最大值对象,其处于两个类的边界处,所以不能很好地代表一个类,则需寻找一个自身密度大的对象,且与Xz距离最远,如图1中E1,相对于一个虚拟类中心C1,E1并不能充分地表示类簇,因此不将E1作为初始类中心,而应该在E1周围选择一个合适的虚点C1作为初始类中心。

图1 E1作为类中心差的情况

本文基于所选的类中心代表能力最强的点E1来构造多个候选对象集合,通过每个集合可以得到一个虚点作为候选类中心。下面给出候选对象集合的定义和求取候选类中心的定义。

定义3设Ca_Sets(1≤s≤m)是第s个候选对象集合,被定义为:

Ca_Sets={Xi∈X|d(Xi,E1)≤s}

(6)

根据式(3),可以计算出Ca_Sets的类中心cas。令Ca_Cluster1={ca1,ca2,…,cam}。

对于任意的两个矩阵对象Xi和Xj,满足0≤δ(Xis,Xjs)≤1,且0≤d(Xi,Xj)≤m。因此,可以根据对象与E1的距离得到m个候选对象集合,第s个集合Ca_Sets是由与E1的距离小于等于s的对象构成的。随着属性s的增加,Ca_Sets集合中的对象数也会逐渐增加。也就是说,cas+1会比cas包含更多的对象信息。因为当s=m时,Ca_Sets=X,此时cas是全部数据对象聚类得到的一个候选类中心。可见Ca_Sets包含过多的对象会削弱cas对第一个类的代表性。可见对于s的取值,并不是越大越好。

采用Microsoft Excel 2016软件对实验数据进行分析及制图，并采用SPSS18.0和Design-Expert 8.0.5对数据进行统计分析，显著水平p＜0.05。

若只考虑DensX(cas)最大,则只能说明cas周围邻居对象数最多,但不能保证cas与E1距离最近以及不能避免cas是边界点,因此还需要考虑到d(cas,E1),并且保证cas与密度最大值对象Xz距离最远。

定义4令Xz(Xz∈X)为密度最大值对象,E1∈X(E1≠Xz)为第一个类中心代表能力最强的点,cas(cas∈Ca_Cluster1)为第一个类的第s个候选类中心,则cas作为类中心的能力为:

Pro_Center(cas)=DensX(cas)+d(cas,Xz)-d(cas,E1)

(7)

令C1=argmaxcas∈Ca_Cluster1Pro_Center(cas),则C1为第一个类中心,即在候选类中心集合中选择一个离密度最大的对象Xz最远、自身密度最高,且更接近于E1的候选类中心作为新的类中心。因为所选择对象的密度越大意味着其周围邻居对象数越多,此外离密度最大值点越远意味着其成为每个类边界点的可能性越小,并且需更加接近于类中心代表能力最强的点。图2为第一个类中心生成过程。

图2 第一个类中心的生成过程

从图2可以看出,空心点表示生成的第一个类中心代表点E1。根据式(6)生成多个候选集合Ca_Sets,其中圈1中的对象表示集合Ca_Set1中包含的对象,同理,圈2和圈3分别表示Ca_Set2和Ca_Set3中包含的对象,且Ca_Set3⊆Ca_Set2⊆Ca_Set1。图2中的五角星是生成的3个候选类中心{ca1,ca2,ca3}。根据定义4得出第一个新的类中心为ca1,记为C1。

定义5给定Xi∈X,k′∈{2,3,…,K},则第k′个类中心代表能力定义为:

(8)

其中,Ck表示第k个类中心。取Pro_Repre(Xi)的最大值所对应的对象作为第k′个类中心代表能力最强点,即:

Ek′=argmaxXi∈X,Xi∉{E1,E2,…,Ek′-1}Pro_Repre(Xi)

则cas(cas∈Ca_Clusterk′)作为第k′个类中心的能力为:

Pro_Center(cas)=DensX(cas)+

(9)

其中,Ck′=argmaxcas∈Ca_Clusterk′Pro_Center(cas)为第k′个类中心。对于其他类中心的选择,本文考虑到对象与所选出的类中心之间的距离,距离越大说明该对象与选出的其他类中心差异越大,能很好地代表一个类中心,同时采用最大最小距离算法用于计算其他类中心。

3.2 算法流程

算法实现流程如下:

算法1IC2SACMD 算法

输入X:由m个属性描述的n个对象矩阵数据集;K:聚类个数

输出数据集X的K个初始类中心C={C1,C2,…,CK}

1.初始化:C = φ;

2.fork′=1to K,do

3.if(k’==1)

4.根据式(3)和式(4)计算数据集X所有对象的平均密度,找出密度最大值的对象记为Xz;

5.对于除Xz之外的其他对象,根据式(5)计算每个对象的代表能力Pro_Repre(Xi)=d(Xz,Xi)×DensX(Xi);

6.获得第一个类中心代表能力最强的点E1=argmaxXi∈X,Xi≠XzPro_Repre(Xi);

7.根据式(6)得出候选对象集合Ca_Sets(1≤s≤m);

8.通过候选对象集合得到候选类中心集合Ca_Cluster1;

9.对于集合Ca_Cluster1中的每个候选类中心,根据式(7)计算Pro_Center(cas)=DensX(Cas)+d(Cas,Xz)-d(Cas,E1);

10.获得第一个类中心C1=argmaxcas∈Ca_Cluster1Pro_Center(cas);

11.else

12.for i=1to n,do

13.根据式(8)求得Xi作为第k′个类中心的代表能力Pro_Repre(Xi);

14.end for

15.获得第k′个类中心代表能力最强的点Ek′=argmaxXi∈X,Xi∉{E1,E2,…,Ek′-1}Pro_Repre(Xi);

16.for k=1to(k′-1),do

18.endfor

19.获得第k′个类中心Ck′=argmaxcas∈Ca_Clusterk′Pro_Center(cas);

20.end if

21.C=C∪Ck′;

22.end for

23.return C.

4 实验结果与分析

为验证本文算法的有效性,在7个不同的真实数据集上进行实验。对数据集进行简单介绍,给出实验所需评价指标,将算法与其他方法进行比较,并对实验结果进行分析。

4.1 实验数据

本文实验使用了7个真实的数据集,其中musk[13]数据集是从UCI上下载,其余数据集是由Veronika Cheplygina整理[14]存放在(http://www.miproblems.org)网站上。mutagenesis[15]和musk是由药物活性预测问题引起的,在这些数据集上,可将每个分子的每个形状看作一个特征向量,由多个形状构成的分子看作一个矩阵对象。mutagenesis根据难易程度分为两种,即文中的mutagenesis1和mutagenesis2。ucsb_breast[16]是一个图像数据集,可以从网址(http://www.bioimage.ucsb.edu/research/biosegmentation)上下载。elephant和tiger是从(http://www.cs.columbia.edu/～andrews/mil/datasets.html)下载的图像数据集[17],可将每张图片的一个分割部分看作一个特征向量,则多个分割部分合成的图片就是一个矩阵对象。component[18]是从(http://www.biocreative.org/tasks/biocreative-i/task-2-functional-annotations/)下载的一个文本数据集,可以将每个段落看作一个特征向量,多个段落组成的一个文本就是一个矩阵对象。表3给出全部数据集的相关信息。

表3 实验中使用的数据集

因为缺少公开的分类型矩阵数据集,且已有的分类型矩阵数据集的维度较低,对于计算属性间距离有比较大的影响,所以本文用数值型矩阵数据集来验证提出算法的有效性。由于数值型数据的属性值是连续的,因此需要对其进行离散化处理。对于musk数据集,数据的属性值是整数型,可以认为是离散型数据,则只需对除musk数据集之外的其余数据集进行归一化处理,归一化公式定义为:

(10)

然后将归一化后的数据集进行均匀离散化处理,将其平均分成10份,相对应的值分别设置为{1,2,…,10}构成了实验所需数据集。

4.2 评价指标

为评价本文提出的初始类中心算法的有效性,使用5个评价指标,即精度(AC)、查准率(PR)、召回率(RE)、标准互信息(NMI)[19]和调整兰德指数(ARI)[20]评价算法的优劣[3]。

4.3 结果分析

为验证本文提出的初始类中心选择算法的有效性,将该算法与一种随机初始化Random算法[3]进行了比较,并与另外两种典型的初始类中心选择算法CAOICACD算法[10]和BAIICACD算法[11]也进行了比较。对于初始类中心算法IC2SACMD、CAOICACD和BAIICACD,只需聚类一次即可。而对于实验中的Random算法,由于该算法采取随机初始化类中心,则需要对每个数据集进行50次聚类,将其均值作为最终的结果。由于目前在分类型矩阵数据上的相关工作较少,本文选用了针对普通分类型数据比较典型的两种初始类中心选择算法CAOICACD和BAIICACD来进行比较,因此需要将本文中的7个真实的数据集进行简单处理,即先将矩阵数据集进行了压缩,每个矩阵对象用频率最高的属性值来表示。在新生成的数据集中,一个对象只有一条记录,然后将后两种算法在新生成的数据集中进行实验。本文实验结果如表4所示,其中,表中加粗字体为不同算法针对每个数据集在不同评价指标上的最优结果。

表4 不同算法在各数据集上的实验结果

从实验结果可以看出,在7个真实数据集上,本文IC2SACMD算法优于Random算法、CAOICACD算法和BAIICACD算法,并在5个评价指标上都产生了比较好的聚类效果,尤其是在mutagenesis2数据集上的聚类效果显著,相比Random算法提高了22%的精度,相比ucsb_breast数据集提高了5%的精度。而CAOICACD算法和BAIICACD算法在不同数据集的5个评价指标上的效果相差不大,仅在tiger和component数据集上相差比较明显,特别是BAIICACD算法在component数据集上达到相对最优,甚至超过了本文算法2%的精度,可见,BAIICACD算法在component数据集上效果更好。但是CAOICACD算法和BAIICACD算法因为数据集进行压缩时,会导致许多信息的丢失,以至于精确度较低。

5 结束语

分类型矩阵数据在实际应用中广泛存在。针对分类型矩阵数据,本文根据属性值的频率定义了矩阵对象的密度和矩阵对象间的距离,扩展了最大最小距离算法,从而实现初始类中心的选择,在此基础上,提出一种面向分类型矩阵数据的初始类中心选择算法。实验结果表明,与传统初始类中心选择算法相比,该算法具有较优的聚类效果。在未来的工作中将结合半监督学习来选择初始类中心。