基于Niederreiter密码体制的抗量子签密方案

王 众,韩益亮

(武警工程大学 密码工程学院,西安 710086)

0 概述

目前,人们的日常生活已经离不开复杂网络与频繁通信,在享受网络通信带来便利的同时,网络安全问题日益突出,如何保障用户的隐私、所发送信息的不可否认性以及通信过程的安全性成为网络通信领域的研究重点。密码学中的签密技术[1]可以提供签名以及加密的功能,其原理是在签密时用发送方的私钥进行签名,用接收方的公钥进行加密,解签密时用发送方的公钥进行签名验证以保证信息的不可否认性,用接收方的私钥进行解密以保证信息的机密性。虽然签密技术能够在一个逻辑步骤内完成签名与加密,为信息提供良好的安全保护,但是,随着量子技术的发展以及量子计算机研究的不断推进,基于经典数论问题的公钥密码方案,如RSA公钥加密算法、椭圆曲线密码(Elliptic Curves Cryptography,ECC)和属性基密码等,未来将无法再为复杂庞大的网络通信提供可靠的安全保证。

近年来,量子技术在密钥安全领域得到应用[2]。现有能够抵御量子计算攻击的密码体制有基于编码的密码体制[3]、基于格的密码体制LWE(Learning With Errors)[4]、基于Hash函数的密码体制[5]以及基于多变量的密码体制[6]。上述密码体制均是在困难问题的基础上而建立,量子计算机与电子计算机在面对这些问题时都不能在有限的资源条件下将其攻破,因此,这类密码体制可以有效抵抗量子计算攻击。其中,基于编码的密码体制具有易于操作以及计算效率较高的特性,因此备受学者们的青睐,该密码体制所依赖的困难问题是码字的译码问题,较早的基于编码的公钥密码算法由文献[7]所编造,其私钥主要为一个二元即约Goppa码的生成矩阵,相对应的公钥为该矩阵被随机处理之后的矩阵。另外一个经典的编码密码算法Niederreiter由文献[8]提出,该算法为文献[7]算法的对偶体制,两者的安全性完全相同,但Niederreiter算法在传信率方面具有一定的优势。截止目前,仍没有能够有效攻击这2种算法的方法。编码密码仍在不断发展之中,为了保证编码密码的安全性、实用性并降低方案的密钥尺寸,由较早的Goppa码、Reed-Solomon码[9],到现在的准循环中密度奇偶校验(QC-MDPC)码[10]、低密度奇偶校验(LDPC)码[11]以及准循环低密度奇偶校验(QC-LDPC)码[12]等,通过优化码字的选择来不断减少编码密码的公钥量,但是,其安全性并未得到实质上的提升。

双公钥加密技术是公钥加密算法中有效提高算法安全性的手段之一,有较多学者将编码密码与双公钥加密思想相结合。文献[13]利用双公钥对文献[7]算法进行改进,安全性有较好的提升,但是其通过双公钥的方式加密,增加了密钥量,实用性不高。文献[14]提出基于QC-LDPC码的双公钥Niederreiter密码方案,由于采用了QC-LDPC码,使得双公钥方案的密钥量有所下降,安全性有较高提升,但是,该方案的密钥量和安全性仍有较大的提升空间。文献[15]提出基于改进Niederreiter密码体制的双公钥加密方案,该方案可以有效抵抗ISD攻击并采用双公钥加密的方式进一步提升安全性,但采用系统码避免双公钥加密的方式降低了运行效率。本文通过对Xinmei签名方案[16]与基于改进Niederreiter密码的双公钥加密方案进行研究,提出一种抗量子签密方案,通过采用系统码的方式在增加方案安全性的同时保证其有效性与实用性。

1 相关知识

1.1 SDP问题

1.2 基于改进Niederreiter的双公钥加密方案

王众等提出的基于改进Niederreiter的双公钥加密方案[15],在第2步加密时对错误向量e的重量进行了隐藏,使得该方案可以较好地抵抗ISD攻击,且其采用双公钥的加密方式提高了安全性。该方案具体步骤如下:

3)解密过程。当接收者收到密文(x1,x2,x3)后,进行以下解密操作:

(1)运用私钥A、B、C、Q以及译码算法β2Ht(),进行第1步解密:

(1)

(2)

(3)

(2)完成第1步解密得到c1后,第2步解密就是普通的Niederreiter密码体制的译码解密。运用私钥S、T和码G1的译码算法β1Ht()进行解密,具体如下:

(4)

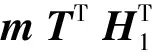
1.3 Xinmei签名方案修正

王新梅教授于1990年在编码密码的基础上提出Xinmei签名方案[16],随后又有许多学者提出了对该方案的攻击以及改进方法,王新梅根据这些攻击方法在2000年提出了针对Xinmei签名方案的修正版[18],以使其可以对选择性明文攻击(简称AW攻击)等进行有效的防御。

设用户在有限域GFq上选择一个(n,k,t)二元即约Goppa码,该码的校验矩阵H的维度为(n-k)×n,生成矩阵G为k×n维,其中,t代表错误向量所允许的最大译码汉明重量。用户再选择2个可逆置换矩阵P与T,其中,P为k×k维,T为n×n维。Xinmei签名方案修正版的具体过程如下:

2)签名过程。待签名信息为kbit的向量m,随机生成一个nbit的向量z,z的汉明重量满足wt(z)≤t,h为Hash函数,发送方进行如下签名:

E(m)=(z+h(z,m)PG)T=c

(5)

签名后产生签密文c,并将(m,c)发送给接收方。

3)解签名过程。当接收方收到(m,c)后,进行如下的签名验证过程:

(1)右乘公钥矩阵V:

D1(c)=cV=[(z+h(z,m)PG)T]T-1HT=

zT-1HT

(6)

(2)运用译码算法Y对D1(c)进行译码得到z。需要注意的是,若wt(z)>t,则说明传输过程有误,无法正确译码,需要发送方重新发送。

(3)右乘公钥矩阵J:

(7)

(4)根据上述结果再进行如下运算:

D3(c)=D2(c)+zW=h(z,m)°

(8)

当且仅当h(z,m)°=h(z,m)时,签名验证过程成功。

1.4 安全模型

根据文献[19-20],本文提出基于编码密码的签密方案的安全模型。

定义2若在下述机密性游戏中,攻击者在任何多项式时间中赢得游戏的优势是可以忽略的,则说明该签密方案满足选择明文攻击下的不可区分性,也即IND-CPA安全。

设多项式时间内的攻击者为α,α赢得下述游戏的优势为Advα,该机密性攻击游戏包括以下步骤:

1)挑战者选择合适参数并运行系统,产生发送者以及接收者的公私钥对(pkS,skS)、(pkR,skR),然后将发送方与接收方的公钥(pkS,pkR)以及发送方的私钥skS发送给攻击者α。

2)攻击者产生2个明文(m0,m1),并将该明文对以及公钥对(pkS,pkR)发送给挑战者。挑战者投掷一枚均匀的硬币,选择(m0,m1)中的一个mb,将公钥对(pkS,pkR)与mb发送给签密预言机,签密预言机将产生的签密文返回给挑战者,由挑战者返回至攻击者α。

3)攻击者收到返回的签密文后,输出1 bit 的b1。当b=b1时,攻击者α赢得游戏,该获胜优势定义为:

(9)

定义3若在下述不可伪造性攻击游戏中,攻击者在任何多项式时间中赢得游戏的优势是可以忽略不计的,则说明本文签密方案在适应性选择消息攻击下满足不可伪造性安全,也即EUF-CMA安全。

设多项式时间内的攻击者为η,η赢得下述游戏的优势为Advη,该不可伪造性游戏包括以下步骤:

1)挑战者选择参数并运行系统,产生发送者S以及接收者R的公私钥对(pkS,skS)、(pkR,skR),然后将接收方的(pkR,skR)与pkS发送给攻击者η,并把发送者的公私钥对(pkS,skS)发送给签密预言机。

2)攻击者可进行签密询问,并验证签密文的合法性。

3)攻击者提交挑战信息m以及伪造的签密文n,并把接收方与发送方的公钥对(pkS,pkR)提交给挑战者,攻击者提交信息(m,n,pkS,pkR)给挑战者。挑战者知道发送方的私钥skS,对签密文n进行解签密运算,产生明文m。针对m,若攻击者之前未对其进行过签密询问,则说明攻击者挑战成功,对明文进行了伪造。

攻击者η的优势可以表示如下:

pkR,m),skR,pkS)]

(10)

2 基于改进Niederreiter双公钥加密的签密方案

2.1 签密方案构造

本文基于改进Niederreiter双公钥加密方案与Xinmei签名方案修正版进行签密方案构造,具体的参数选择、公私钥生成以及签密解签密过程如下:

(2)c=(z+f(r||m)PAG1A)TA。

(3)FB·c→(x1,x2,x3)。

(4)Output (x1,x2,x3)。

3)解签密过程,具体计算如下:

(3)Y(D1(c),t1)→z

Whilewt(z)≤t1continue

Else Receive error occurred,sender A resend

(5)D3(c)=D2(c)+zW=f(r||m)。

Outputm。

Else output⊥。

2.2 正确性分析

当接收者收到签密文(x1,x2,x3)后,首先需要使用自己的私钥对其进行解密,解密成功后得到向量c,由签密步骤2可知,c的产生是由Xinmei签名算法对函数f的结果f(r||m)进行签名所得,其中,随机向量z是由随机向量r和明文m通过安全Hash函数所产生。

3 安全性分析

3.1 不可伪造性

Pr[B]=Pr[X1∩X2∩X3]≤1/(qf+qSC+qH)·

(11)

其中,qSC、qDSC、qH、qf分别代表攻击者η所能进行的签密询问、解签密询问以及对预言机H和f询问的最大次数,分别设立4个询问列表Hlist、flist、SClist、DSClist来对询问进行记录。

1)预言机H询问。攻击者η进行H询问,向H预言机中输入r||m,首先查询表中是否有相应记录,存在记录则返回给攻击者;不存在则生成z,将其记录在表Hlist中并返回给攻击者。

2)预言机f询问。攻击者η进行f询问,向f预言机中输入r||m,首先查询表中是否有相应记录,存在记录则返回给攻击者;不存在则生成v,将其记录在表flist中并返回给攻击者。

4)解签密询问(DSC)。向解签密预言机进行询问时,输入签密文n,首先查看表DSClist中是否有相应记录m,若存在则返回给询问者,否则执行解签密算法得到r,通过r的值,在表Hlist、flist中进行查询得到明文m。

不可伪造性攻击游戏的过程如下:

1)运行签密系统,生成必要参数。

2)攻击者进行预言机H询问和预言机f询问。

3)攻击者提交明文m与伪造的签密文n,并对n进行解签密询问,若询问返回结果为m,并且没有对其进行过签密询问,则说明攻击者成功赢得游戏。

证明在签密询问时,首先查询表SClist中是否有相应记录,若存在相应记录则返回给询问者,否则需要产生对应的结果。在没有记录的情况下,要调用预言机H与f来产生相应的z与v的值,若H与f中已经存在对应于m的z或v的值,则说明模拟过程失败,需要预言机SC、H与f对同一明文进行成功的询问,这样才能完成签密询问,将此记为事件X1,其发生的概率为:

Pr[X1]=1/(qf+qSC+qH)

(12)

在解签密时,输入签密文n,首先查看表DSClist中是否有相应记录m,若存在则返回给询问者,不存在则执行解签密算法得到r,由r的值在表Hlist、flist中进行查询找到相应的明文m,若没有相应的记录,则说明模拟失败。将通过r的值可在表Hlist、flist中进行查询找到明文m记为事件X2,其发生的概率为:

Pr[X2]=(qH/22n)·(qf/22n)=(qH·qf)/22n

(13)

(14)

由上述分析可知,攻击算法B需要在以上3个相互独立的事件都成立的前提下才可以成功,其优势表示如下:

Pr[B]=Pr[X1∩X2∩X3]≤1/(qf+qSC+qH)·

综上,本文签密方案满足EUF-CMA安全。

3.2 机密性

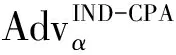
证明将本文签密方案所涉及的SDP问题实例交由攻击算法K尝试解决,攻击算法K作为攻击者α在游戏中的挑战者,而α作为攻击算法K的子程序。具体步骤如下:

1)攻击算法B得到SDP问题实例中发送方以及接收方的公私钥对(pkS,skS)、(pkR,skR),然后将发送方与接收方的公钥(pkS,pkR)以及发送方的私钥skS发送给攻击者α。

2)攻击者产生2个明文(m0,m1),并将该明文对以及公钥对(pkS,pkR)发送给挑战者。挑战者投掷一枚均匀的硬币,选择(m0,m1)中的一个mb,将公钥对(pkS,pkR)与mb发送给签密预言机,签密预言机将产生的签密文返回给挑战者,由挑战者返回至攻击者α。

3)攻击者收到返回的签密文后,输出1 bit 的b1作为猜测。

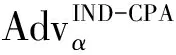
(15)

因此,本文签密方案满足IND-CPA安全。

3.3 相关攻击分析

针对编码密码体制,目前较为有效的攻击手段包括直接译码攻击和信息集译码攻击(ISD)等。

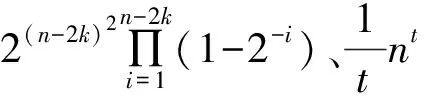
本文签密方案采用基于改进Niederreiter的双公钥加密方案实现加密功能,在机密性上能够为签密方案提供较好的保障。

4 效率分析

4.1 加密方案优势

本文签密方案通过基于改进Niederreiter的双公钥加密方案实现加密功能,其采用系统码进行构造,以双公钥加密方式进行加密,密钥量会有所增加但仍在可接受的范围内,安全性得到较大提升。将文献[14-15]中的2种方案进行比较,结果如表1所示。基于改进Niederreiter的双公钥加密方案在第2步加密时采用了改进版Niederreiter方法,对重量t有隐藏功能,允许其选择维度较小的码字而达到与普通Niederreiter同样的安全级别。

表1 文献[14-15]方案中的第2步加密密钥尺寸对比

从表1可以看出,在达到282bit安全级别时,文献[14]方案的密钥尺寸为20 904 bit,而文献[15]方案为5 040 bit,密钥尺寸有明显下降,在2128bit安全级别下两者具有同样的效果,即隐藏重量t能够显著提升本文签密方案的效率。

4.2 密钥与密文量分析

在有限域GFq上选取二元系统码G1、G2,维度分别为(120,40)、(80,40),进行如表2所示的对比。由表2可以看出,本文签密方案在私钥量与密文量方面相比先签名后加密的方法有较大的提升。私钥量下降是因为在签密方案构造时,其中n×n维的矩阵T在签名以及加密中共用,从而减少了一个n×n维的矩阵,也即14 400 bit的私钥量。在密文量方面,先签名后加密或者先加密后签名的方法会产生签名以及密文,而本文签密方案是对签名进行加密,只有对签名进行正确验证后才可以得到相应的明文信息,签密方案的签密文即对签名进行加密后的密文(x1,x2,x3),由1.2节对加密方案的描述可知该签密文的大小为120 bit,即本文方法的密文量相比先签名后加密的方法减少了50%。

表2 4种方案的密钥与密文分析

Table 2 Key and ciphertext analysis of four schemes bit

方案公钥量私钥量密文量文献[15]方案1120032000120Xinmei签名方案1600019200120先签名后加密方案2720051200240本文签密方案2720036800120

5 结束语

本文通过对Niederreiter密码体制进行研究,采用基于改进Niederreiter的双公钥加密方案来构造抗量子签密方案。相比改进Niederreiter方案以及基于QC-LDPC码的双公钥Niederreiter密码方案,该加密方案在安全性方面得到较大的提升,且其采用系统码来保证双公钥的加密方式不会带来过大的密钥量。在此基础上,本文将基于改进Niederreiter的双公钥加密方案与Xinmei签名方案相结合,提出一种基于编码密码的签密方案。分析结果表明,该方案能够满足EUF-CMA与IND-CPA安全,相比先签名后加密或者先加密后签名的方案,其私钥量和密文量均较低,在后量子时代具有良好的使用前景。下一步尝试在该签密方案中增加如混合签密、代码签密等功能,以适应更加复杂的网络环境。