基于种子变异潜力的模糊测试方法
王 乔,宋礼鹏
(中北大学大数据学院,太原 030051)
模糊测试是一种通过向目标系统或软件提供大量自动生成的畸形数据来发现漏洞的软件安全测试方法。模糊测试时,被测程序的代码覆盖率越高,发现漏洞的机会越大。自第一代模糊测试技术[1]出现以来,研究人员为提高代码覆盖率提出了覆盖率导向策略,以覆盖率信息指导测试进行。在收集覆盖率信息方面,目前主要有两种策略:第一种是收集已测试种子的覆盖率信息,如AFL(American fuzzy loop)对覆盖新路径的种子进行变异[2];AFLfast[3]以覆盖不被频繁覆盖的路径数量作为判断种子变异潜力高低的条件;AFLgo以种子覆盖路径和目标之间的距离来决定种子变异的优先级[4];FairFuzz则通过收集对分支的命中情况,选择命中稀有分支的种子进行变异[5]。第二种策略则是利用程序分析技术,如CollAFL[6]和Vuzzer[7]使用了静态分析技术[8]来提取控制流和数据流情况,而Driller[9]则通过利用符号执行[10]技术处理复杂约束。
覆盖率导向策略的主要问题是如何得到更精确的覆盖率信息以及如何判断种子变异潜力的高低。在选择优质种子时,变异潜力的高低应该是衡量种子优质程度的最主要标准,而诸如选择覆盖新分支的种子或选择覆盖稀有路径的种子进行下一轮变异等策略往往会导致变异结果不够理想,这是因为种子效果好和种子变异潜力高并不等价,新分支可能在下次变异后不被覆盖而失去价值,或者新分支可能导向一个错误处理块或程序终止块,这种类型基本块并不具有高的漏洞挖掘价值,因此覆盖这种类型分支的种子价值较低、变异潜力也较低。
针对上述问题,提出了一种基于种子变异潜力分析的模糊测试方法,首先提取程序控制流图,以基本块入口地址作为其标记,考虑基本块自身情况以及互相之间调用情况来赋予其权值。同时,在每一代种子运行结束后,根据种子覆盖路径附近未被覆盖的基本块权值情况以及种子运行时资源开销情况来计算适应度,从而筛选优质种子,投入下一代变异。本文策略能体现种子变异潜力主要由于以下两个方面。
(1)以种子覆盖路径附近未被覆盖的基本块数量作为衡量标准之一,这样得到的高适应度种子通过变异到达未探索基本块概率大,并且可能到达的未探索基本块数量多。
(2)对基本块进行赋权操作,将变异潜力体现在底层基本块上。对于两个不同的未覆盖基本块,后继块多的基本块往往意味着如果通过变异实现对该基本块的覆盖,则通过该基本块到达新基本块的可能情况越多并且可能性越大,因此覆盖该基本块的价值就越大。
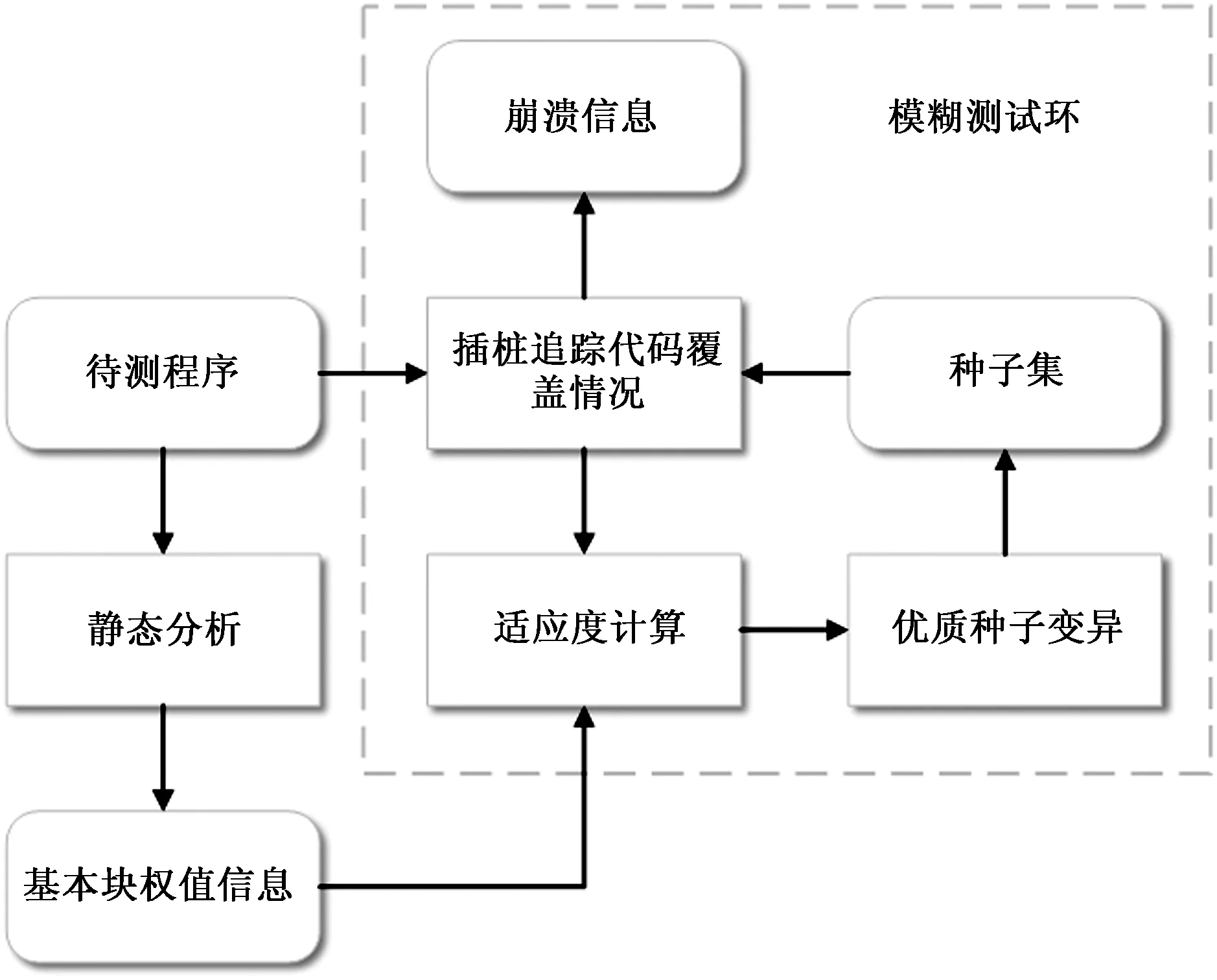
图1 PAFuzz结构Fig.1 Structure of PAFuzz
1 基于种子变异潜力的模糊测试技术
模糊测试技术整体设计如图1所示,首先在AFL的基础上增加静态分析模块,提取该程序中不同基本块信息和控制流图,根据权值计算策略计算基本块权值。其次对被测程序进行插桩,追踪种子在测试期间的路径信息以及覆盖情况,结合基本块权值,根据适应度函数计算种子适应度,选择适应度大的部分种子投入变异池进行变异,利用生成的新一代种子进行下一轮测试,迭代上述过程,并基于以上策略设计了模糊测试工具PAFuzz。所用方案一方面在适应度计算时加入路径潜力信息,提高了适应度函数的筛选效果,另一方面以入口地址标记基本块,以前驱和后继两个基本块的入口地址组成的元组标记分支,避免了传统模糊测试策略标记分支时不同分支间的碰撞问题。
1.1 基本块赋权
为了得到更有效更精确的路径信息,在开始测试前先对被测程序进行静态分析,提取控制流和数据流信息,以便在后续测试过程中能更有效地计算种子的覆盖情况。在静态分析方面,选择使用IDA python插件对被测程序进行分析,提取函数基本块的入口地址,出口地址和调用情况。
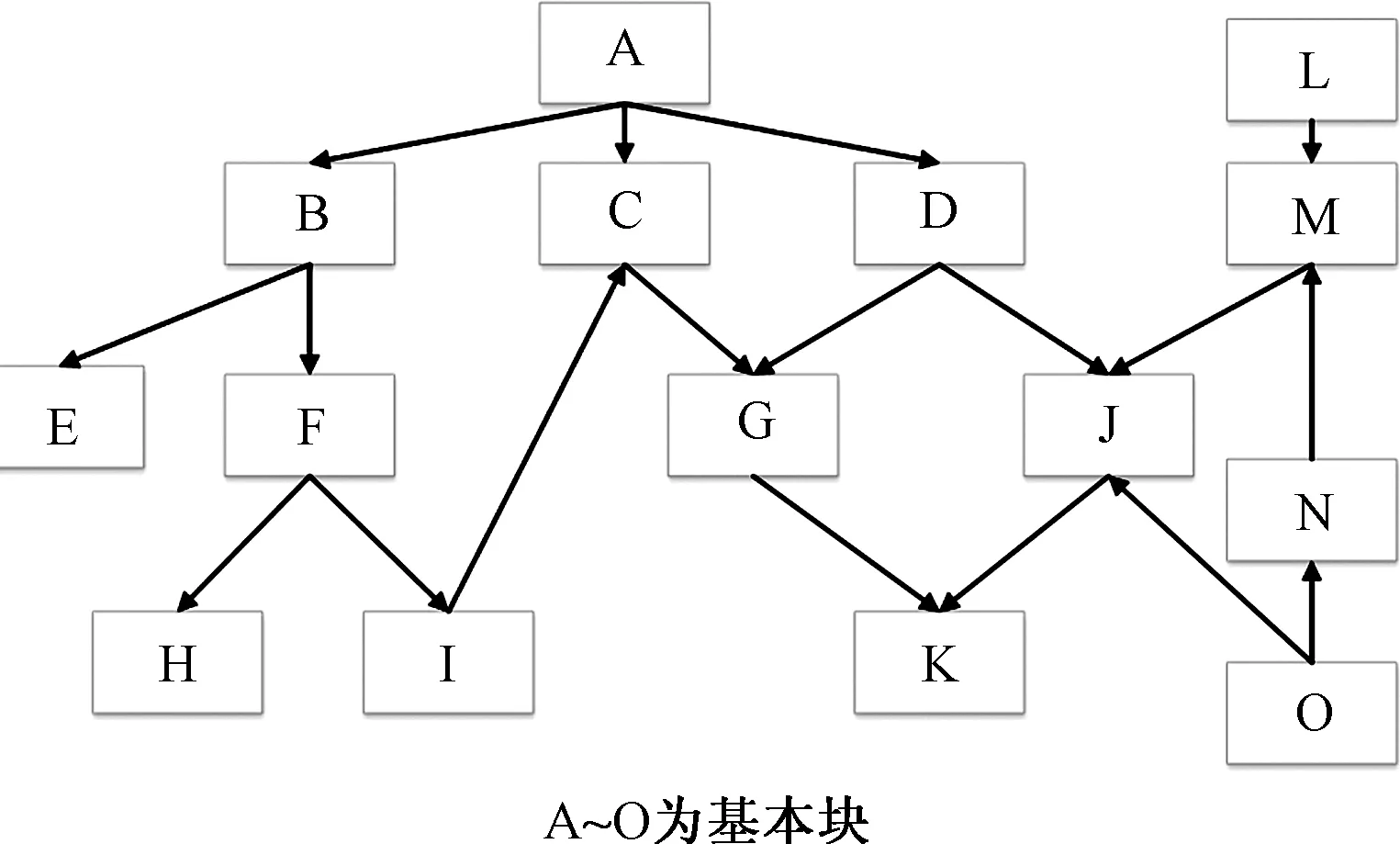
图2 控制流图Fig.2 Graph of Control flow
图2为控制流图,每个方块代表一个基本块,A代表主函数Main,箭头表示调用关系。传统的覆盖率导向策略主要考虑种子的优质程度,例如,对于种子a,如果a覆盖的路径为(A、B、F、H)而分支{F->H}为新分支,则将a视为优质种子,分配更多变异机会。但一方面新分支{F->H}可能在变异之后不被覆盖,另一方面H是一个程序终止块,无后继块不具备任何变异潜力,因此这样的筛选策略效果并不理想。权值计算方法综合考虑两个方面的信息。
(1)离根节点(孤立节点)越近的基本块权值参数越高,而每远一层,参数减半,在大多数情况下,处于越高层的基本块往往意味着可能存在更多的子孙块,例如基本块B,对覆盖B的种子进行变异,可能到达的基本块有E、F、H、I、C、G、K,而对覆盖G的种子进行变异则可能覆盖的基本块为K。虽然处于低层的基本块F实际上比处于高层的C和D存在更多的子孙块,但认为通常情况下高层的基本块存在更大变异潜力。由于同一基本块可能存在于不同路径中导致其在程序中所处层次不同,本文以距离根块最短的路径作为基本块位置;
(2)对于每一个基本块来说,后继块的个数越多,则代表对覆盖该基本块的种子进行变异,可能到达的不同基本块越多,而无后继块的基本块,除该块本身可能存在的漏洞以外,无任何变异潜力,因为无论如何变异,只要到达这个基本块,则程序运行走到终点,这种基本块的典型代表就是错误处理块,当程序运行满足不了既定条件时,转向错误处理块、报错并终止程序,考虑到基本块本身可能存在的漏洞可能使其存在一定价值,在计算基本块后继时进行了加1操作,可以有效提高适应度函数的效果。
此外,还考虑到孤立块以及不在根块的子孙集合中的基本块的情况,如图2所示的L、M、O、N,对于孤立块,则赋予其和根块一样的权值参数,而对于既是根块A的子孙块,又是孤立块L、O的子孙块,以其在主函数下的位置情况赋予其权值。
定义入口地址的集合为Ast,基本块的集合为BBAst,程序入口地址为ADD,基本块权值参数集合为WHbb.Ast,基本块权值集合为FWbb.Ast,考虑到要计算基本块处于的最高层情况,采用层次遍历的算法计算基本块权值,具体算法描述如算法1所示。
算法1
for bb in BBAst:
if bb.Ast==ADD and len(list(bb.preds()))==0:
WHbb.Ast=n
FWbb.Ast=WHbb.Ast*(len(list(bb.succs()))+1)
V.append(bb.Ast)
T.append(bb)
while len(T)!=0:
cb=T.popleft
for cbb in cb.succs():
if cbb.Ast not in V:
WHcbb.Ast=WHcb.Ast/2
FWcbb.Ast=WHcbb.Ast*(len(list(cbb.succs()))+1)
V.Add(cbb.Ast)
T.Add(cbb)
而对于孤立块和非根块子孙集合中的基本块,则执行算法2处理。
算法2
for bb in BBAst
if bb.Ast!=ADD and len(list(bb.preds()))==0:
WHbb.Ast=n
FWbb.Ast=WHbb.Ast*(len(list(bb.succs()))+1)
V.append(bb.Ast)
T.append(bb)
while len(T)!=0:
cb=T.popleft
for cbb in cb.succs():
if cbb.Ast not in V:
WHcbb.Ast=WHcb.Ast/2
FWcbb.Ast=WHcbb.Ast*(len(list(cbb.succs()))+1)
V.Add(cbb.Ast)
T.Add(cbb)
else:
pass
1.2 适应度函数
适应度函数的计算是最能体现种子潜力的部分,对于模糊测试环来说十分重要。一旦一个种子生成,那么该种子能否参与下一代变异取决于该种子的适应度函数大小。采用二进制插桩的方法,收集种子运行过程中对代码块的覆盖情况。考虑图2所示的例子,如果种子S1经过的路径为(A、B、F、H),种子S2经过的路径为(A、C、G、K),基础权值参数为n,而测试过程中覆盖过的基本块为A、B、C、F、G、H、K,如果考虑种子覆盖基本块的权值,则S1权值和为(4+1.5+0.75+0.125)n=6.375n,S2权值和为(4+1+0.5+0.125)n=5.625n,因此S1覆盖路径比S2有更大变异潜力,但是对于这种策略,对于覆盖较高权值基本块的种子将不断获得变异机会,测试前期能够实现对附近分支多的种子分配更多变异机会,实现覆盖率的快速提高,但是由于所有基本块权值固定,覆盖较高权值的基本块无论其附近基本块覆盖情况如何,将不断获得变异机会,导致测试后期种子多样性降低,不利于测试持续高效进行。因此在该策略的基础上提出收集种子覆盖路径附近基本块情况,由其中未被覆盖的基本块权值和来体现路径种子变异潜力,则S1覆盖路径周围未探索基本块为D、E、I,权值和为(1.5+0.25+0.25)n=2n,S2覆盖路径周围未探索基本块为D,权值和为1.5n,因此S1覆盖路径比S2有更大变异潜力。
除此之外,考虑到计算机资源开销问题,处理时间和种子文件大小也是影响适应度的两个因素,在处理效果相同时,处理时间较短和文件大小较小的种子往往意味着更高的处理效率和更小的资源开销,因此对于一代种子S,将以下两个参数加入到适应度函数计算中。
Tseed=time(s)/avet(S),s∈S
(1)
Lseed=length(s)/avel(S),s∈S
(2)
式(1)表示种子s在处理时间上的优质程度,式(2)表示种子s在大小上的优质程度,其中avet(S)和avel(S)代表所有种子平均时间开销和平均长度。结合基本块权值信息,可以计算得到种子的适应度函数,如式(3)所示:
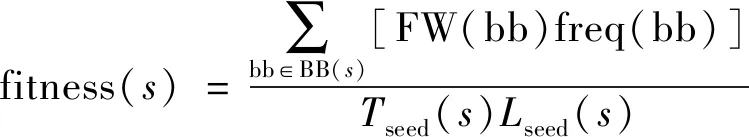
(3)
式(3)中:BB(s)代表s周围未覆盖的基本块集合;FW(bb)为bb的权值;freq(bb)为bb出现在s周围的次数,选择每一代中适应度最高的部分种子进行下一代变异。
1.3 变异策略
AFL在种子变异方面主要采用了按位翻转(将二进制位1变成0或0变成1)、整数加减、特殊内容替换、自动生成或用户提供的token插入和文件拼接五种策略,主要结合遗传算法[11]实现种子变异,主要策略如下。
1.3.1 交叉变异
如图3所示,从优质种子中随机选取两个,对随机选择的一段比特位进行交换,得到两个子代种子。
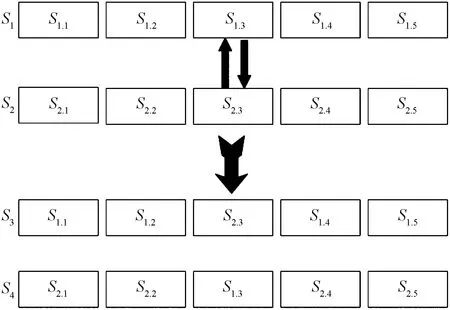
图3 交叉变异Fig.3 Cross variation
1.3.2 替换变异
如图4所示,对优质种子的随机选择的一段比特位,使用特殊数据或随机数据进行替换。
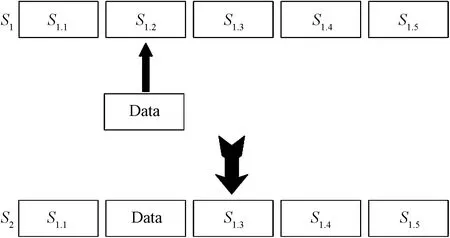
图4 替换变异Fig.4 Replacement variation
1.3.3 大规模突变
适应度函数筛选优质种子不可避免会导致种子池在后期多样性降低,无论交叉还是替换操作都不能再给种子质量带来有效提高,因此当程序在一定轮数之后未发现新块,则选择执行大规模突变,提升种子池多样性并一定程度恢复种子探索新路径能力。
2 实验
为了测试所用模糊测试方案的效果,将本文方案在LAVA-M数据集[12]和真实Linux程序上进行了测试,实验结果与目前广泛使用的模糊测试工具AFL(2.52b)在漏洞发现能力、覆盖率、漏洞发现速度和输入数据总大小方面进行了对比,测试环境为Ubuntu系统,并为其配置了4-core的CPU和4GB内存,测试初始种子集相同。
2.1 漏洞挖掘能力
发现漏洞的能力是模糊测试工具优劣的集中体现,因此比较了24 h内发现漏洞情况,AFL使用QEMU对二进制程序进行插桩,被测程序选择LAVA-M数据集,漏洞发现情况结果如表1所示。同时,将本文方案和AFL在真实Linux应用进行了对比测试,结果如表2所示。
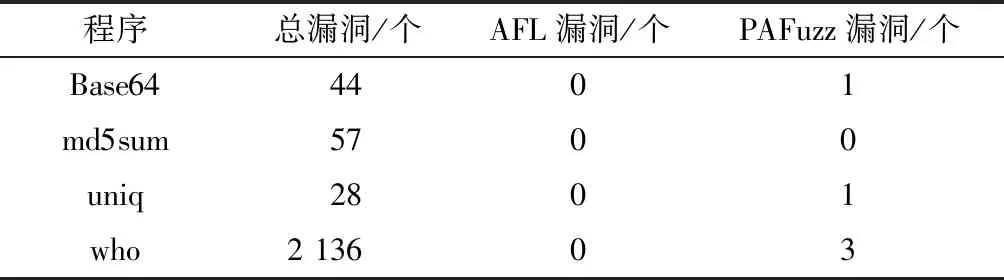
表1 LAVA-M上漏洞发现能力对比Table 1 Comparison of vulnerability discovery capabilities on LAVA-M

表2 真实程序上漏洞发现能力对比Table 2 Comparison of vulnerability detection capabilities on real programs
由表1、表2可知,在变异策略基本相同的情况下,基于本文策略的模糊测试工具在漏洞挖掘能力方面相比于以是否发现新分支作为种子优劣标准AFL有明显提高,充分说明本文策略筛选出的种子变异后测试效果优于AFL。
2.2 覆盖率情况
代码覆盖率情况是衡量技术性能的重要指标,一方面能反映筛选策略的优劣程度,另一方面体现变异策略的效率,在对上述程序进行测试时,收集并统计了本文方案和AFL在24 h内覆盖的总路径情况,结果如表3所示。

表3 覆盖率情况对比Table 3 Comparison of coverage
由表3可知,被测程序的路径覆盖率平均提高了14.73%,这是由于所筛选策略将种子变异后可能到达的新基本块情况作为衡量标准,变异后种子覆盖新路径的可能性比AFL更大,在变异策略基本相同的情况下,所筛选策略得到的覆盖率情况明显优于AFL。
2.3 输入数据
对24 h内测试过的种子总大小进行统计,结果如表4所示。分析结果可知,相比于AFL,PAFuzz将种子大小和运行速度作为衡量标准之一,整个测试过程中生成的测试用例空间开销更小,效率更高。
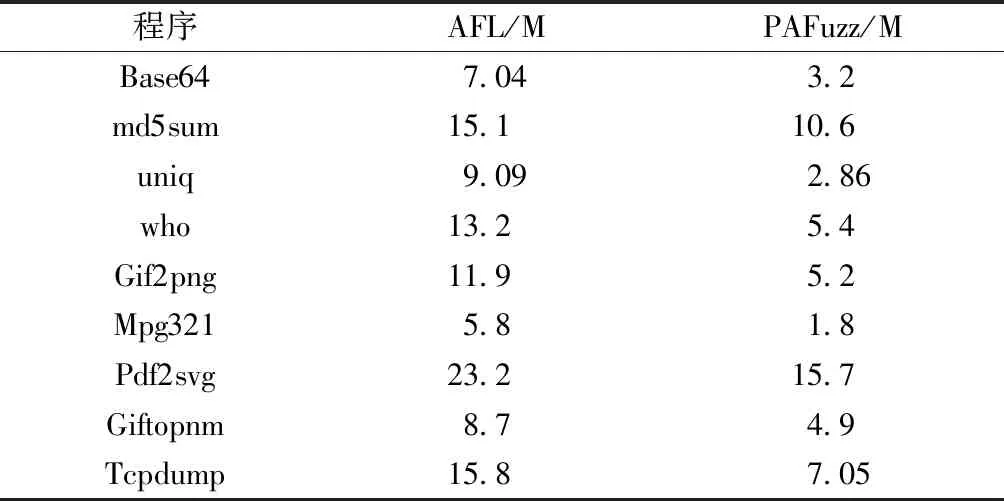
表4 测试用例总大小对比Table 4 Comparison of test case total size
2.4 漏洞发现速度
为了对比整个实验过程中AFL和PAFuzz在24 h内各个时间段漏洞发现情况以及整体漏洞发现趋势,以2 h为间隔对两个方案漏洞发现情况进行采样,对比了两个方案的漏洞发现速度,对比结果如图5所示。分析图5可知,由于本文方案筛选出的优质种子执行速度快变异潜力大,变异后可能覆盖的新路径多,因此本文方案能够快速提升代码覆盖率并在测试前期触发更多漏洞。同时,AFL由于使用简单的遗传算法,导致种子在后期的差异性变小,替换变异和交叉变异的效果大幅度减弱,发现漏洞能力严重下滑,而本文方案则有效避免了这一情况,同时由于存在大规模突变机制,可以有效提高测试后期种子多样性,因此在后期发现漏洞的能力也优于AFL,更加证明本文策略的有效性。

图5 漏洞发现情况对比Fig.5 Comparison of vulnerability discovery
3 结论
针对传统模糊测试在种子筛选时数据粗糙、算法简单、无法真正分辨种子变异潜力的问题,提出一种改进方案,主要是结合基本块的位置和后继基本块的数量分析基本块的变异潜力,追踪种子覆盖路径附近未被覆盖的基本块情况,综合种子的处理速度和大小,给出其适应度函数值。实验表明在相同时间内,本文方法在漏洞发现数量、漏洞发现速度和代码覆盖率方面都有所提高,同时还避免了覆盖率导向技术中存在的碰撞问题。
在下一步的研究中,将结合诸如污点分析[13]、符号执行等技术对变异策略进行进一步优化以应对程序中的复杂约束,覆盖程序深处代码块。

