连续弯梁桥盆式支座摩擦滑移特性分析

许汉铮,李晓涛,刘 青,潘 宏,陈武浩,胡 眺

(1.长安大学公路学院，西安 710054；2.中设设计集团股份有限公司，南京 210001)

与直线桥相比，弯桥因其在适应复杂地形条件，舒缓交通压力等方面的天然优势，使其伴随着城市交通线中匝道桥的设计施工充分发展起来[1]。弯桥受力复杂，弯扭耦合效应明显，梁体横向位移过大，严重时会引起主梁侧倾，同时伴随着支座脱空、伸缩缝剪切破坏、桥墩的环向裂缝、挡块挤压破坏等病害[2]。桥梁支座是重要的传力构件，支座的破坏会引起结构传力路径的改变或者中断，对桥梁结构承载力和安全运营会产生较大影响。

Steelman等[3]建立全桥的有限元模型，研究了支座摩擦滑移效应对桥梁整体受力性能的影响；Huth等[4]通过对瑞士的铁路桥支座体系进行长期监测和实验室模拟测试，分析了盆式支座服务32年后各项力学特性；Lomiento等[5]提出了一个计算支座摩擦效应的模型，同时经试验验证发现循环荷载产生的摩擦升温会使研究者过高的估计支座的摩擦耗能能力。

拟采用大型有限元分析软件建立盆式橡胶支座的三维实体模型和混凝土弯梁桥有限元模型，分析盆式支座力学性能，并且通过与交通运输部公路科学研究院完成的2.5 MN(兆牛)盆式橡胶支座的承载力试验结果进行对比，验证有限元模型的准确性，为后续进行支座摩擦滑移特性分析奠定基础。

1 盆式橡胶支座的基本结构

普通盆式橡胶支座主要由顶板、不锈钢冷轧钢板、聚四氟乙烯板、中间钢板、黄铜密封圈、橡胶板、钢盆、锚固螺栓、防尘圈和防尘围板组成。双向活动支座的结构示意图如图1所示。

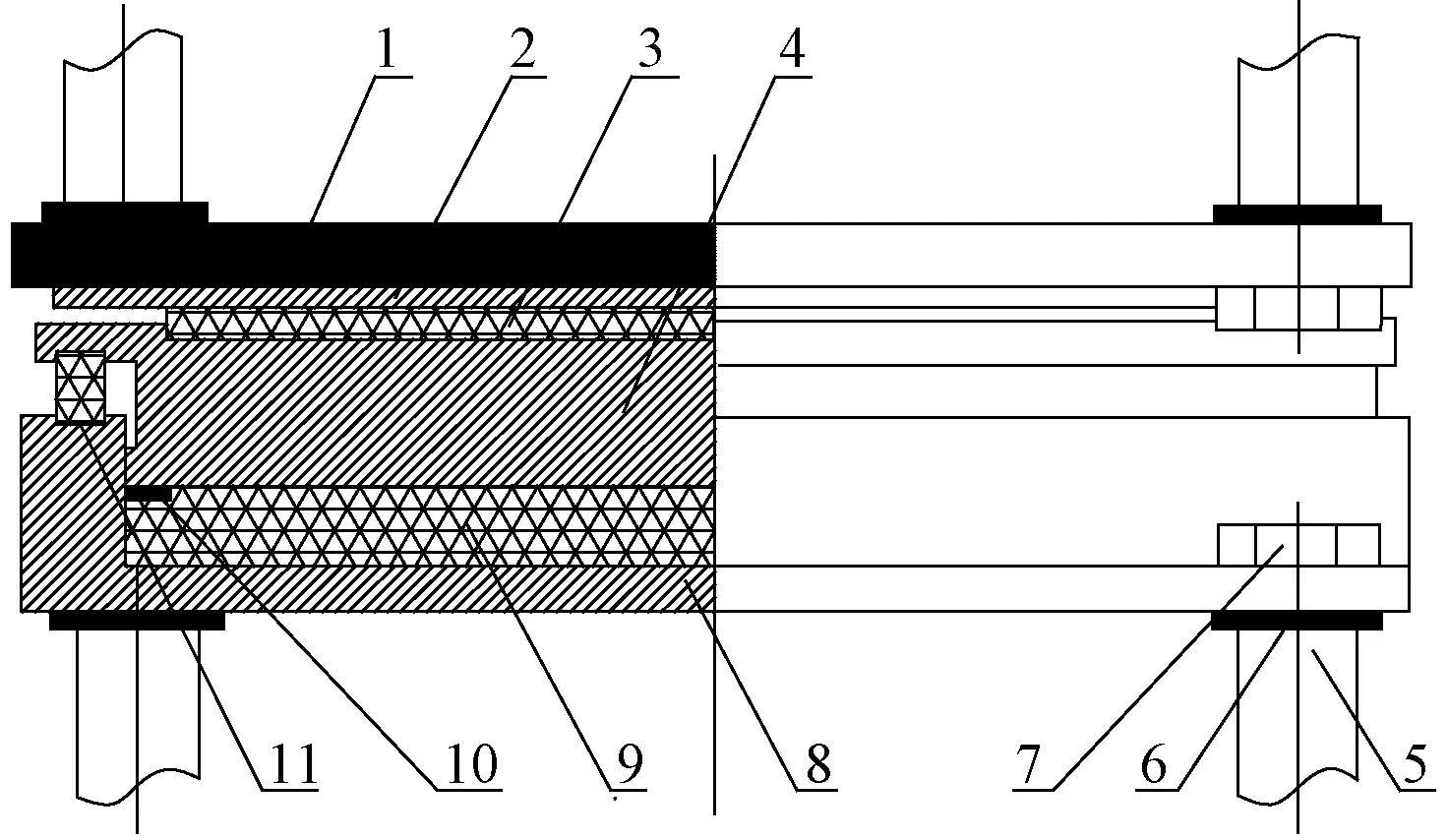
1为顶板;2为不锈钢冷轧板；3为聚四氟乙烯板；4为中间钢板；5为套筒；6为垫圈；7为锚固螺栓；8为钢盆；9为橡胶板；10为黄铜密封圈；11为防尘圈图1 双向活动结构示意图Fig.1 Diagram of two-way active structure

盆式橡胶支座中顶板和梁底采用固结的方式，这种联结方式使得主梁受力后底板和支座上顶板同步变形，这样支座顶板会将结构上部力传给聚四氟乙烯板，接下来荷载顺次传递给承压橡胶和支座底板，然后传递给桥墩等下部构造，而在此过程中支座则通常主要承受压应力。当支座承受压力时，在盆底应力集中现象比较明显，产生较高的局部应力，而该数值较盆环应力要大很多[6-9]。

分析可知，盆式橡胶支座主要通过橡胶块的承载力、盆环约束力、聚四氟乙烯板与不锈钢滑板之间的摩擦滑移来完成传力与变形。

2 盆式支座有限元模型

以往对盆式支座的有限元模拟过于简化，大多有限元模型通常不建立聚四氟乙烯板结构，只考虑精轧不锈钢板与聚四氟乙烯板接触面之间的接触刚度，摩擦系数等参数。但是盆式支座的水平位移是依靠聚四氟乙烯板和精轧不锈钢板之间的滑动实现的，在上部荷载作用下发生变形也会影响其他构件应力分布情况，所以聚四氟乙烯板的工作性能直接影响支座的滑动性能，是进行摩擦滑移必不可少的结构之一。

借助通用有限元分析软件ANSYS对普通盆式橡胶支座进行精细化模拟，建立包括上顶板，聚四氟乙烯板、钢盆的实体模型，以此分析普通盆式支座的基本力学特性。

2.1 建模的基本假定

盆式支座承载力可分为33个等级，选择公路桥梁盆式橡胶支座支(SX表示双向活动)座，支座高度129 mm；盆内承压橡胶块高度26 mm，直径360 mm；支座顶板尺寸为L×L=590 mm×590 mm；支座盆底厚度17 mm；盆环厚度40 mm。聚四氟乙烯板厚度7 mm，直径300 mm。(以上mm均表示厘米)支座结构示意图如图2所示。

图2 盆式支座结构尺寸示意图Fig.2 Diagram of structural dimensions of basin bearing

为正确模拟支座结构同时提高计算速度，根据工程实际和理论计算对普通盆式支座做以下假定：①假定支座底板与支座垫石刚接;②支座上顶板与主梁刚接，同时变形，主梁上部荷载均匀传递到支座上顶板;③橡胶四周和钢盆内环内侧、中间钢衬板四周和钢盆内侧均采用接触分析。

2.2 盆式支座材料模拟

2.2.1 聚四氟乙烯材料特性

聚四氟乙烯板与铸铁之间的摩擦系数很低，容许抗压强度为30 MPa。支座模型材料有铸钢、橡胶，聚四氟乙烯板三种，其中铸钢力学特性比较明确，分析时不考虑钢盆的塑性变形。聚四氟乙烯板的弹性模量约为铸钢材料的1/100，但其厚度小，变形量相对于其他构件很小，因此可以忽略聚四氟乙烯板的变形，在有限元计算中将其看作线弹性材料，钢盆与聚四氟乙烯板均采用Solid185来模拟。

2.2.2 承压橡胶块材料特性

基于统计热力学理论及应变能函数理论，国内外学者提出了不同的模型来模拟橡胶。比如基于应变能函数理论的模型有：Mooeny-Rivlin模型、Yeoh模型、Valanis-Landel模型、Ogden模型等；基于统计热力学理论的模型有：高斯链网络模型、非高斯链网络模型、混合模型等[10-11]。各种模型特点以及使用范围如表1所示。

表1 橡胶材料模型及其使用范围Table 1 Rubber material model and its application range

工程上多采用Mooney-Rivlin本构模型来模拟橡胶的本构特性，其应变能密度函数模型为[12]

(1)

式(1)中：W为应变势能；I1、I2、I3为变形张量不变量；Cij、dk和N为材料常数，可由材料试验确定，也可以通过经验公式拟合；对于不可压缩的橡胶材料，I3=1。

典型的二项三阶展开式可以表示为

W=C10(I1-3)+C01(I2-3)

(2)

在模拟钢盆中橡胶特性时选用两参数的Mooney-Rivlin模型来研究支座橡胶层的本构关系。采用经验公式法确定橡胶Mooney-Rivlin模型参数。橡胶材料具有各向同性，其剪切模量G与弹性模量E的关系如式(3)所示：

(3)

式(3)中：μ为泊松比。

假设橡胶为不可压缩材料，即泊松比μ趋近于0.5，则G=E/3。橡胶剪切模量和弹性模量与Mooney-Rivlin模型参数的关系分别为

G=E/3=2(C10+C01)

(4)

E=6C10(1+C01/C10)

(5)

橡胶邵氏硬度HA与弹性模量E的经验公式为

E=(15.75+2.15HA)/(100-HA)

(6)

在小变形范围内，C01/C10取0.25时可以达到理想的拟合效果，根据测得的橡胶硬度，代入式(4)、式(5)中，即可求得Mooney-Rivlin模型的两个参数。

将根据经验公式来确定C10和C01的值，橡胶的硬度取为60。根据式(4)和式(5)可求得：C10=0.482 5 MPa和C01=0.120 6 MPa，因橡胶具有不可压缩性，其泊松比取为0.499 8。分析可知，支座相关参数取值如表2所示。

表2 支座材料参数Table 2 Bearing material parameters

2.3 支座接触面模拟

ANSYS中面-面接触单元可以有效模拟各实体接触面摩擦行为。其中橡胶与钢盆接触属于刚体-柔体接触，钢材被视作刚性目标面，采用ANSYS中接触单元TARGE170单元进行模拟，橡胶则被视作柔性接触面，采用ANSYS中接触单元CONTA173来模拟，目标面与接触面相互对应，从而形成接触对。同时钢盆与橡胶之间的摩擦系数取0.7；而聚四氟乙烯板与精轧不锈钢板的摩擦系数则取0.03。通过控制单元特性KEYOPT(12)参数来控制接触方式。

2.4 支座有限元模型

建立支座三维实体模型，主要分析盆式支座力学特性以及各接触面之间摩擦滑移特性，将盆底看做刚接在墩台上，采用完全固接的约束方式。盆内橡胶与盆环内侧、橡胶顶面与中间钢板、橡胶底面与钢盆底面之间均为接触面，采用接触分析。建立的模型如图3所示。

图3 盆式橡胶支座实体模型及网格划分图Fig.3 Solid model and mesh drawing of basin rubber bearing

3 盆式橡胶支座基本性能分析

盆式橡胶支座的传力路径比较明确，假定支座顶板与梁底完全固接，同时受力，同时变形。竖向荷载由钢盆内的承压橡胶块承担，水平荷载只要依靠聚四氟乙烯板与不锈钢滑板之间的摩擦力承担。

3.1 聚四氟乙烯板受力特性分析

聚四氟乙烯板厚度很小，主要提供水平位移，有横向位移限制的抗压弹性模量和抗压比例极限都远大于无侧向约束值。模型按照支座实际建模，聚四氟乙烯板厚度4/7嵌固在中间钢板顶部凹槽内，此时聚四氟乙烯板抗压比例极限约为99 MPa。图4、图5分别为聚四氟乙烯板应力和变形云图。

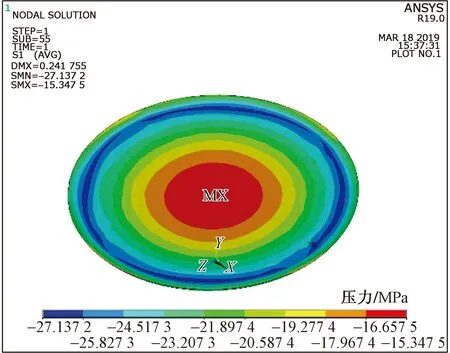
图4 聚四氟乙烯板应力云图Fig.4 Stress cloud chart of polytetrafluoroethylene plate

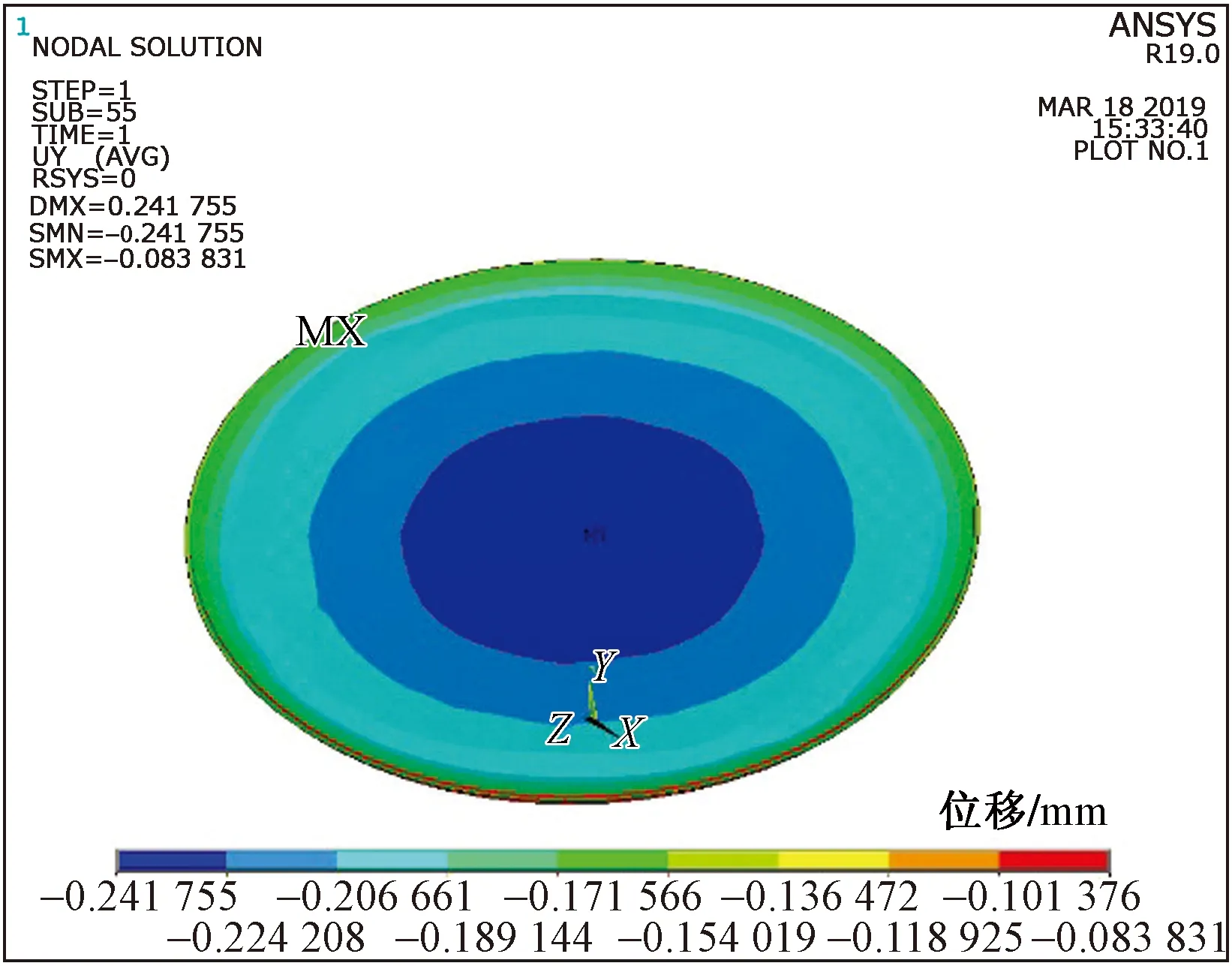
图5 聚四氟乙烯板变形云图Fig.5 Polytetrafluoroethylene plate deformation cloud picture

从图4应力分布来看，聚四氟乙烯板全截面受压，最大等效应力为27 MPa，小于容许应力值30 MPa，聚四氟乙烯板正常工作。聚四氟乙烯板中心的应力值较小，向外侧环形增加，边缘的应力最大。聚四氟乙烯板的最大应力远远小于抗压比例极限，塑性变形不足以发生，因此在有限元分析中，线弹性模型的基本假设是正确的。

从图5位移云图的分布规律可知，聚乙烯四氟板中心变形较大，向外侧环形减小，边缘位移最小。聚四氟乙烯板的位移值为0.08～0.24 mm，对支座整体变形影响不大。

3.2 橡胶块受力特性分析

橡胶块是盆式支座主要承压构件，用来承担支座反力，传递水平位移和转角，因此要求橡胶块具有可靠的承压性能和较小的弹性压缩。在模型中，橡胶的直径采用360 mm，而其抗压弹性模量为4 000 MPa，容许应力值为25 MPa。

图6 承压橡胶板主应力云图Fig.6 Principal stress nephogram of pressure rubber plate

图7 承压橡胶板变形云图Fig.7 Deformation nephogram of pressure rubber plate

在设计荷载作用下最大主应力为22.65 MPa，小于容许压应力值25 MPa。由图6可知，橡胶块压应力分布规律为橡胶板中心等效压应力较小，向边缘呈环形增加，在橡胶块与盆环接触面上出现局部应力集中现象。应力集中点沿橡胶边沿均匀分布。

图8 橡胶板边缘应力分布Fig.8 Edge stress distribution of rubber plate

从橡胶块的位移云图(图7)可以看出，橡胶的竖向变形为0.067～0.26 mm，压缩变形占支座总变形量的1%～2%。最大变形出现在橡胶块底部边缘，且各个方向的位移相差不大，分布均匀。位移较大的点与应力集中点的分布位置基本相同。提取橡胶块边沿上各点应力值，如图8、图9所示，分析其分布规律。

图9 橡胶板上下表面应力分布Fig.9 Stress distribution of upper and lower surface of rubber plate

由图8可以看出,橡胶边缘应力分布规律呈锯齿形，应力有正有负，出现拉应力可能是因为盆环变形。由图9可以看出,橡胶上边缘的应力值大于底边边缘的应力值，上下表面应力值分布规律一致。橡胶上下表面应力值沿直径的分布规律相同，上表面与下表面应力最大值均在橡胶板中心附近，最大相差4 MPa。

图10 盆环应力变形云图Fig.10 Stress-deformation nephogram of basin ring

3.3 盆环受力特性分析

盆环应力应变等效云图如图10所示，应力分布如图11所示。

由图10可知，盆环等效应力分布在9～83 MPa，盆环在钢盆中橡胶提供的侧向压力作用下承受拉力，最大拉应力出现在橡胶顶面与盆环接触面上。盆环竖向压缩变形很小，最大为0.37 mm，径向位移最大为0.014 mm，小于容许变形量0.22 mm。沿盆环高度提取不同高度盆环等效应力值，结果如图11所示。由图11可知，不同高度上盆环应力分布规律相同，压应力出现在盆口。

3.4 盆底受力特性分析

盆底应力云图和应力分布如图12、图13所示。

由图12可以看出，下支座板在设计荷载作用下，最大应力为70.2 MPa，低于铸钢材料的容许应力值。提取从盆底中心沿直径到钢盆边缘的应力值，如图13所示。由图13可以看出，距盆底中心1/2R范围内压应力向边缘逐渐增大，但增大幅度较小。180～220 mm盆环处，应力突然增大，最大值为103.23 MPa。由于盆环处出现较大的应力集中。钢盆底部在此发生微小翘曲，产生拉应力。

由表3可以看出，支座各部分受力均满足设计要求，正常使用荷载下有稳定的受力和变形能力。

图11 盆环应力分布Fig.11 Stress distribution of basin ring

表3 设计竖向荷载作用下各部分最大应力、变形Table 3 Maximum stress and deformation of each part under design vertical load

4 有限元模型验证

为了验证计算的正确性以及模型是否与实际支座的约束条件、受力特性一致，采用交通运输部公路科学研究院完成的2.5 MN盆式橡胶支座的承载力试验结果与有限有模型计算结果进行对比。为了说明验证的可行性，首先对试验条件与有限元模拟条件做一个对比，对比结果如表4所示。

表4 试验条件与有限元参数对比Table 4 Comparison of test conditions and finite element parameters

表4所示的基本试验条件与有限元模拟的基本条件一致，因此试验数据与有限元计算结果相互验证是可行的。

交通运输部公路科学研究院对2个2.5 MN的盆式支座进行了成品验证性试验，加载分为预加载和正式加载。正式加载前对支座进行了三次预加载，预加荷载为2 500 kN，在支座底板与顶板之间布置位移计。正式加载时分10步进行，加载到3 500 kN。在有限元计算时将荷载步分为10步，以均布荷载的形式施加在支座顶板。提取每一荷载步对应的竖向压缩变形值，得到荷载-变形曲线并与试验结果进行对比，结果如图14所示。

图14 理论与试验结果对比Fig.14 Comparison of theoretical and experimental results

由图14可以看出，该型号支座的竖向压缩变形理论最大值为0.62 mm，试验最大值为0.65 mm，二者均满足支座竖向压缩容许值。试验测得的最大压缩变形量与有限元计算结果相差4.8%，属于可接受误差范围。试验结果与理论计算得到的荷载-变形曲线的变化规律也比较吻合。盆环径向变形量较小，在设计竖向荷载作用下盆环径向变形值为0.015 mm，文中计算结果为0.014 mm，二者相差不大。因此可以证明该有限元计算模型能够准确地模拟实际支座的受力和变形。

5 结论

(1)盆式支座依靠钢盆内三向受压橡胶块承受竖向荷载，橡胶块变形使与之接触的盆环受拉，支座底板与盆环接触面存在局部应力集中现象，但最大应力值远小于铸钢材料屈服强度，不影响支座正常工作。聚四氟乙烯板在设计荷载作用下产生的变形很小，这种微小变形对中间钢板以及橡胶板应力分布的影响很小，分析支座力学特性时可以将聚四氟乙烯板作为线弹性材料。

(2)盆式支座整体最大应力值、竖向压缩变形量、盆环径向变形量均满足设计要求。盆式支座有较大的安全储备，受力稳定，变形量小，一般不会发生承载力极限破坏，支座水平受力特性显得至关重要。

(3)将支座有限元计算结果与试验值进行了对比，结果表明支座竖向压缩量的有限元计算结果与试验值相差0.03 mm，误差不大，说明本文模型可以准确地模拟盆式支座的受力和约束条件，为后续进行支座摩擦滑移特性分析奠定基础。