溶洞对隧道结构变形与受力特征的影响研究
——以大方隧道为例
郭 瑞,黎 晨,郑 波,舒 波
(1.中铁西南科学研究院有限公司,成都 611731;2.中铁十五局集团有限公司,上海 200040;3.成都地铁运营有限公司,成都 610036)
随着中国高速公路、高速铁路以及城市轨道交通的快速发展,隧道及地下工程所占的比例逐渐增大,而地质条件复杂、施工风险高等问题日益突出,其中,岩溶隧道因周围溶洞分布的隐蔽性、不确定性给隧道建设带来了巨大困难[1]。因此,研究溶洞分布对隧道结构变形受力的影响对指导工程建设具有极为重要的意义。
在岩溶隧道灾害防治方面,学者针对高速公路和高速铁路岩溶隧道突涌水灾害开展了一系列研究[2-7],获得了颇有价值的成果。李术才等[8]通过模型试验研究了隧道开挖诱发隐伏溶洞破裂突水致灾的机制;管鸿浩[9]结合现场量测和数值模拟,研究了施工过程中充水溶洞对隧道衬砌变形与受力的影响;何翊武等[10]通过理论分析研究了隧底溶洞对衬砌结构的影响;李海港等[11]通过数值模拟研究了隧道施工与前方大型溶洞的应力叠加效应;易菁等[12]和陈福全等[13]通过力学理论推导,给出了隧道与溶洞相互作用影响下的应力解析解;戴自航等[14]通过数值模拟分析了溶洞位置对岩溶区高速公路路堤稳定性的影响;徐海清等[15]研究城市地铁沙漏型岩溶地面塌陷机理及防治措施。前人述研究为岩溶隧道的深入研究奠定了重要基础,但是对于溶洞分布位置以及溶洞尺寸大小对隧道结构位移与内力的影响规律研究较少,特别是确定溶洞分布的最不利位置以及溶洞对隧道显著影响的区域方面研究甚少,缺少从设计施工角度出发的定量研究。
鉴于此,通过综合考虑溶洞分布位置、尺寸大小以及与隧道净距等不同因素,建立二维有限元模型,研究不同溶洞分布对隧道结构变形与受力特征的影响,最后通过对比分析研究了溶洞对隧道影响显著的区域,得出溶洞分布的最不利位置。研究成果可为岩溶隧道设计施工提供科学参考和借鉴。
1 数值模型及分析工况
1.1 数值模型建立
以成贵铁路大方隧道为背景,该隧道所处地层为岩溶发育区,大方隧道埋深90 m,隧道跨径14.4 m,隧道围岩条件为Ⅴ级,采用双层管棚超前加固,加固厚度为40 cm,初支采用H175型钢做拱架,二衬为55 cm厚度的C35钢筋混凝土,大方隧道断面如图1所示。
为减小边界效应,模型以隧道中心为原点,左右及隧道底部以下各取100 m,总体尺寸为200 m×190 m,图2为有限元计算模型。左右边界施加水平约束,底部边界上施加垂直约束,顶部为自由边界。溶洞采用圆形进行近似,围岩及加固区采用平面单元模拟,初支采用梁单元模拟,溶洞及隧道的开挖、隧道支护结构的施做采用单元的杀死与激活功能实现。二衬作为安全储备,不参与计算,初支承担70%的荷载,考虑到锚杆和注浆加固对围岩的改善作用,模拟时适当提高加固区围岩的参数。数值计算中,第一步形成有溶洞情况下的初始地应力场,并清除初始位移场;第二步进行隧道的开挖计算,开挖后释放30%的荷载;第三步激活衬砌单元并释放余下70%的荷载,同时提高围岩加固参数。数值计算参数如表1所示。
1.2 计算工况
综合考虑溶洞分布位置、尺寸大小d及与隧道净距L等不同因素,共计48种工况,表2为计算工况统计。同时为对比分析,计算了无溶洞工况,根据溶洞在隧道顶部、侧部和底部的不同位置,分别对每种工况下隧道结构的变形和受力进行对比分析。
2 计算结果分析
2.1 溶洞于隧道顶部计算结果分析
2.1.1 溶洞对支护结构变形影响
图3为隧道顶部溶洞在不同净距下结构位移曲线。从图3(a)结构最大水平位移曲线可看出,随溶洞直径d增大,结构水平位移逐渐增大,同时与无溶洞工况相比,当溶洞直径d≤0.4D时,顶部溶洞对结构的水平收敛位移影响较弱,此外随溶洞与隧道结构净距L的增大,水平收敛位移逐渐减小。从图3(b)拱顶竖向位移可看出,当溶洞直径d≤0.4D时,拱顶产生竖向沉降变形,且变形量值与无溶洞工况接近,而当d>0.4D时,拱顶沉降由负值变化正值,说明拱顶结构产生了向外挤出变形,这是由于拱顶溶洞达到一定大小时,使得水平围岩压力大于拱顶竖向围岩压力,造成支护结构顶部产生了向溶洞一侧的挤压变形。同时可看到,两者均在净距L<0.3D时,结构位移变化尤为剧烈,特别是当净距L=0.1D时,溶洞大小与结构的位移影响最为显著。从图3(c)拱底位移来看,随着拱顶溶洞直径d增大,拱底结构位移逐渐减小,这是由于拱顶溶洞规模的增大,竖向地层压力减小,故开挖后拱底地层回弹减弱。

图1 大方隧道断面设计图Fig.1 Section design of Dang’fang tunnel

图2 数值计算模型Fig.2 Numerical calculation model
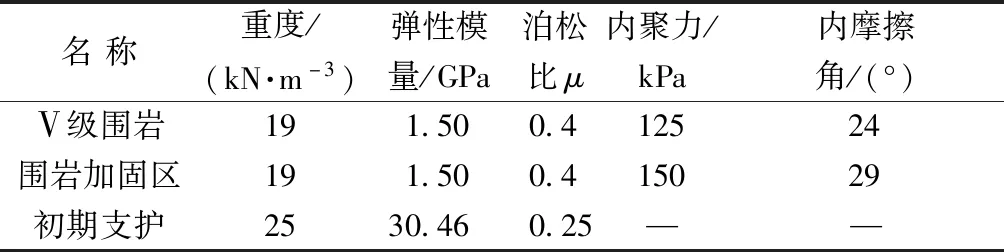
表1 围岩及支护结构的物理参数Table 1 Mechanical parameters of surrounding rock and support structure
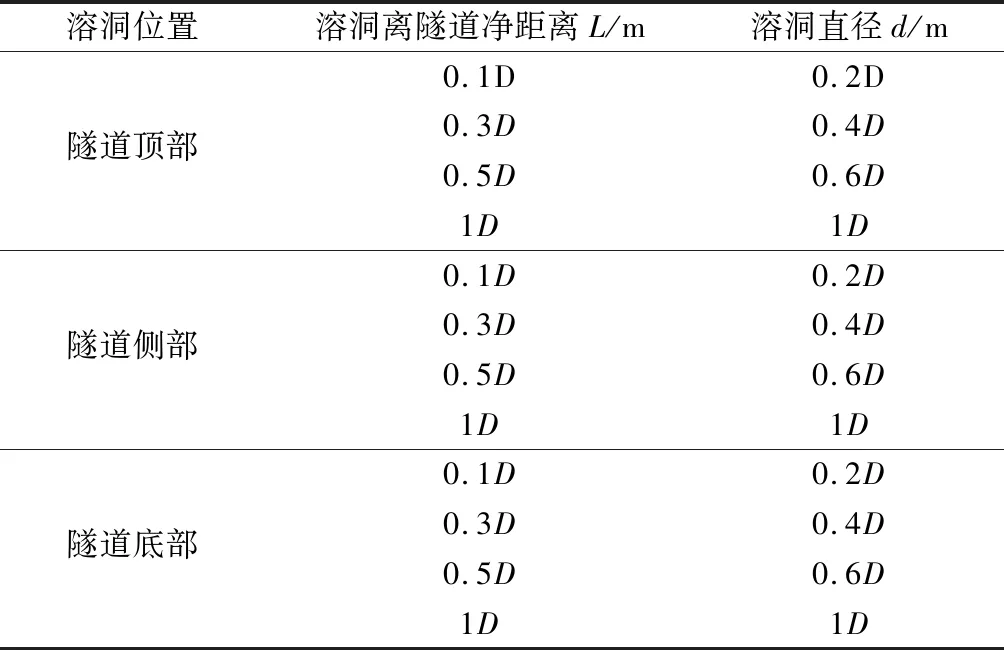
表2 计算工况统计Table 2 Calculation condition statistics
注:D为隧道直径14.4 m。
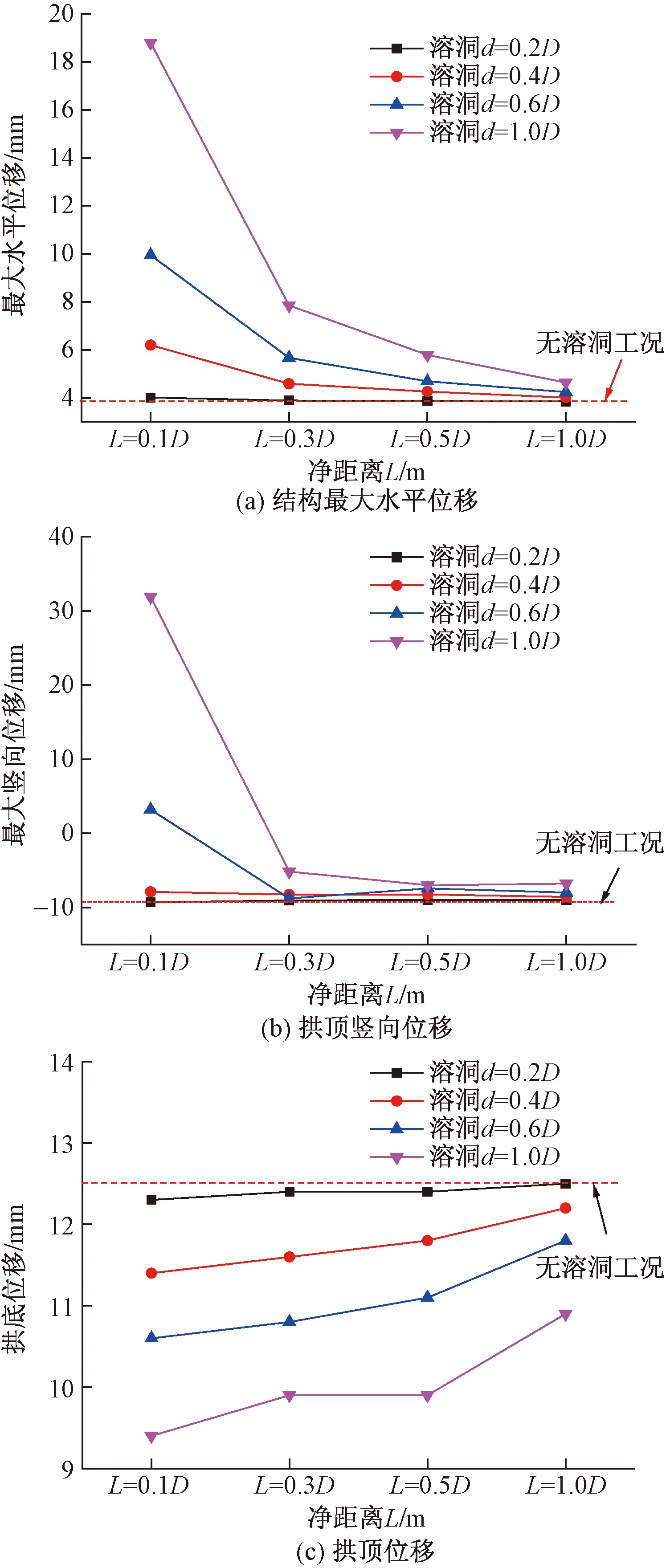
图3 不同净距下结构位移曲线Fig.3 Structural displacement curve at different distances
2.1.2 溶洞对支护结构内力影响
图4为隧道顶部溶洞在不同净距下结构内力曲线。从图4(a)结构最大轴力可看到,与无溶洞工况对比隧道顶部溶洞使得隧道结构的轴力均有所减小,且随隧道顶部溶洞的增大,结构轴力逐渐减小。图4(b)为隧道结构最大剪力曲线,当净距L<0.3D时,隧道结构剪力变化较为明显,与无溶洞相比较,剪力最大增大200%,而当净距L≥0.3D时,与无溶洞相比较,剪力基本维持稳定值,同时从溶洞大小来看,当溶洞直径d≤0.4D,剪力值与无溶洞相比较基本一致。图4(c)为衬砌结构最大弯矩曲线图,弯矩曲线变化规律与剪力曲线相似,当净距L<0.3D时,结构弯矩变化较为明显,与无溶洞相比较,弯矩最大增大403%,而当净距L≥0.3D时,弯矩值基本维持稳定不变。同时从溶洞大小来看,当溶洞直径d≤0.4D,弯矩值与无溶洞相比较基本一致。
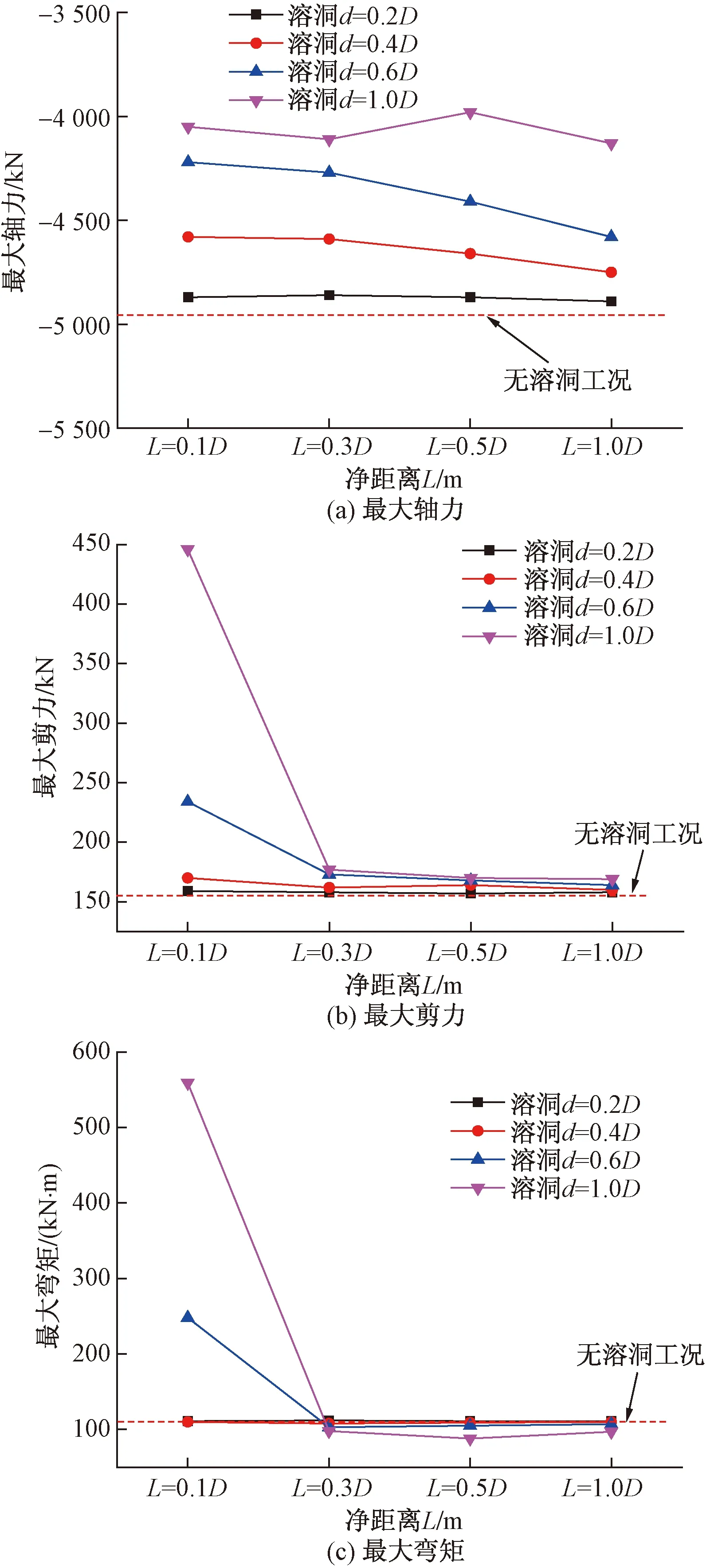
图4 结构内力变化曲线 Fig.4 Structural internal force curve
综合分析可知,当溶洞与隧道净距L≤0.3D时,溶洞直径d≥0.6D时,顶部溶洞对衬砌结构的形与受力影响较大,且在隧道拱顶结构表现最为显著。
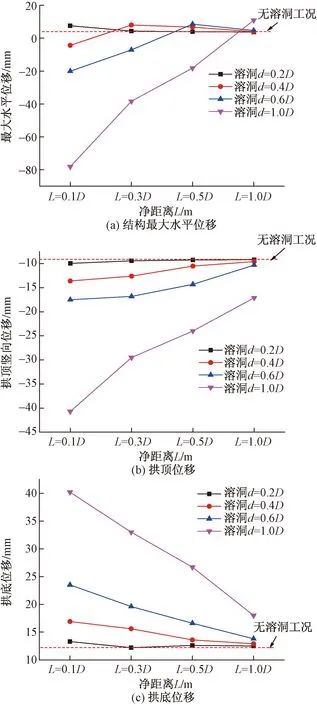
图5 不同净距下结构位移曲线Fig.5 Structural displacement curve at different distances
2.2 溶洞于隧道侧部计算结果分析
2.2.1 溶洞对支护结构变形的影响
图5为隧道侧部溶洞在不同净距下结构位移曲线,水平位移正值表示隧道向内部产生收敛变形,负值表示产生隧道向围岩方向产生变形。由图5(a)衬砌最大水平位移曲线可知,在同一净距L下,随溶洞直径d增大,衬砌结构水平位移数值由正值逐渐变为负值,特别是溶洞直径d=1D时,最大变形达到近-80 mm,而当d≤0.4D时,衬砌水平方向位移较小,这是由于侧部溶洞的存在,使得隧道支护结构在侧部溶洞方向易产生应力集中,造成结构向溶腔方向发生变形,随溶洞与衬砌结构净距L的增大,衬砌结构的水平位移逐渐较小。从图5(b)拱顶竖向位移可以看出,拱顶最大竖向位移规律与衬砌结构最大水平位移变化规律基本相同。同样当溶洞直径d=1D时,拱顶竖向位移较大,从量值上来看,侧溶洞对衬砌的水平位移远大于其对拱顶结构的竖向位移。从图5(c)拱底位移来看,随侧部溶洞直径d增大,拱底结构位移逐渐增大,随净距L的增大,拱底位移逐渐较小。
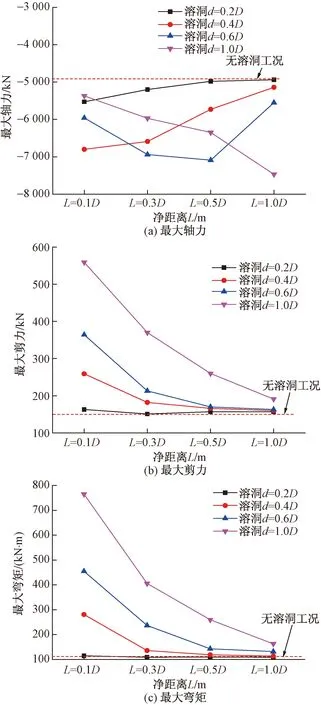
图6 结构内力变化曲线Fig.6 Structural internal force curve
2.2.2 溶洞对支护结构内力的影响
图6为隧道侧部溶洞在不同净距下结构内力曲线。从图6(a)衬砌结构最大轴力曲线可知,与无溶洞对比侧部溶洞使得支护结构轴力均有所增大,但轴力增大值不超过80%,同时结构均处于受压状态,未产生拉应力。从图6(b)最大剪力变化曲线可知,随净距L的增大,剪力值逐渐减小,趋于无溶洞时衬砌的剪力值;同一净距L下,剪力值随溶洞直径d增大而逐渐增大。从图6(c)最大弯矩变化曲线可知,与剪力变化规律一致,最大弯矩随溶洞净距L的增大逐渐减小,且在同一净距下,随溶洞直径d的增大,弯矩逐渐增大。

图7 不同净距下结构位移曲线Fig.7 Structural displacement curve at different distances
综合分析可知,当净距L≤0.3D时,溶洞直径d≥0.6D时,侧部溶洞对衬砌结构的形与受力影响较大。
2.3 溶洞于隧道底部计算结果分析
2.3.1 溶洞对支护结构变形的影响

图8 结构内力变化曲线 Fig.8 Structural internal force curve
图7为隧道底部溶洞在不同净距下结构位移曲线。从图7(a)衬砌最大水平位移曲线可看出,同样随溶洞与衬砌结构净距L的增大,衬砌结构的水平位移逐渐较小,同时可看到在同一净距L下,随着溶洞直径d增大,衬砌结构水平位移逐渐增大。从图7(b)拱顶竖向位移曲线可看出,拱顶竖向位移曲线呈水平状,随溶洞直径d增大,拱顶竖向位移均呈减小状态。从图7(c)拱底位移来看,当溶洞直径d≤0.6D时,拱底结构位移为正值,说明支护结构产生了向隧道内部的回弹变形,当溶洞直径d=1D时,净距L<0.5D时拱底位移为负值,最大产生了约50 mm的竖向沉降,这是由于隧底因溶洞空腔的存在,地层承载力减弱,加之隧道开挖支护的施加,造成拱底结构产生下沉。
2.3.2 溶洞对支护结构内力的影响
图8为隧道底部溶洞在不同净距下结构内力曲线。从图8(a)最大轴力变化曲线可知,曲线基本呈水平状态,但在净距L=0.1D时,溶洞直径d=1D时,支撑轴力减小30%。总体来看,拱底下部溶洞存在对衬砌轴力影响较弱。从图8(b)最大剪力变化曲线可知,仅在溶洞直径d=0.2D,净距L=0.1D时剪力减小。同时可看到,当净距L<0.3D时,最大剪力随溶洞直径d的增大而增大,与无溶洞相比较,剪力最大增大80%,最大剪力产生在拱底位置附近。当净距L≥0.3D时,最大剪力值基本维持稳定。从图8(c)衬砌结构最大弯矩变化曲线可知,结构最大弯矩随溶洞净距L的增大逐渐减小,且在同一净距下,随溶洞直径的增大,弯矩逐渐增大。同样当净距L<0.3D时,衬砌结构弯矩变化较为明显,与无溶洞相比较,弯矩最大增大近400%,而当净距L≥0.3D时,弯矩值基本维持稳定值,同时从溶洞大小来看,当溶洞直径d≤0.6D,弯矩值与无溶洞相比较增幅较小。
综合分析可知,当净距L≤0.3D时,溶洞直径d≥0.6D时,对衬砌结构变形与受力影响较大,同时从受力位置来看,拱底衬砌结构内力较大。
2.4 结果对比分析
综合以上分析可知,当溶洞直径d≥0.6D,且与隧道净距L≤0.3D时,溶洞对隧道结构变形与内力均影响显著。鉴于此,为研究相同条件下三种溶洞位置对隧道结构的影响大小,在此进行了不同位置结构内力与塑性区的对比分析。
图9为不同溶洞位置结构内力对比曲线。从图9中隧道结构轴力、剪力和弯矩数值对比来看,溶洞位于隧道侧部时对结构内力影响最大,溶洞位于隧道顶部和底部时,影响相对较弱,同时,剪力和弯矩曲线变化趋势基本一致。图10为溶洞直径d=0.4D、净距L=0.3D的塑性区分布云图,从云图可看到,在同一工况下,溶洞位于隧道侧部时,靠近溶洞一侧的塑性区显著增加,并与溶洞周围塑性区贯通连成一片,而溶洞位于隧道顶部和底部时,塑性区均未贯通。综合对比可知,可得出隧道稳定性最不利的溶洞位置是隧道侧部溶洞。
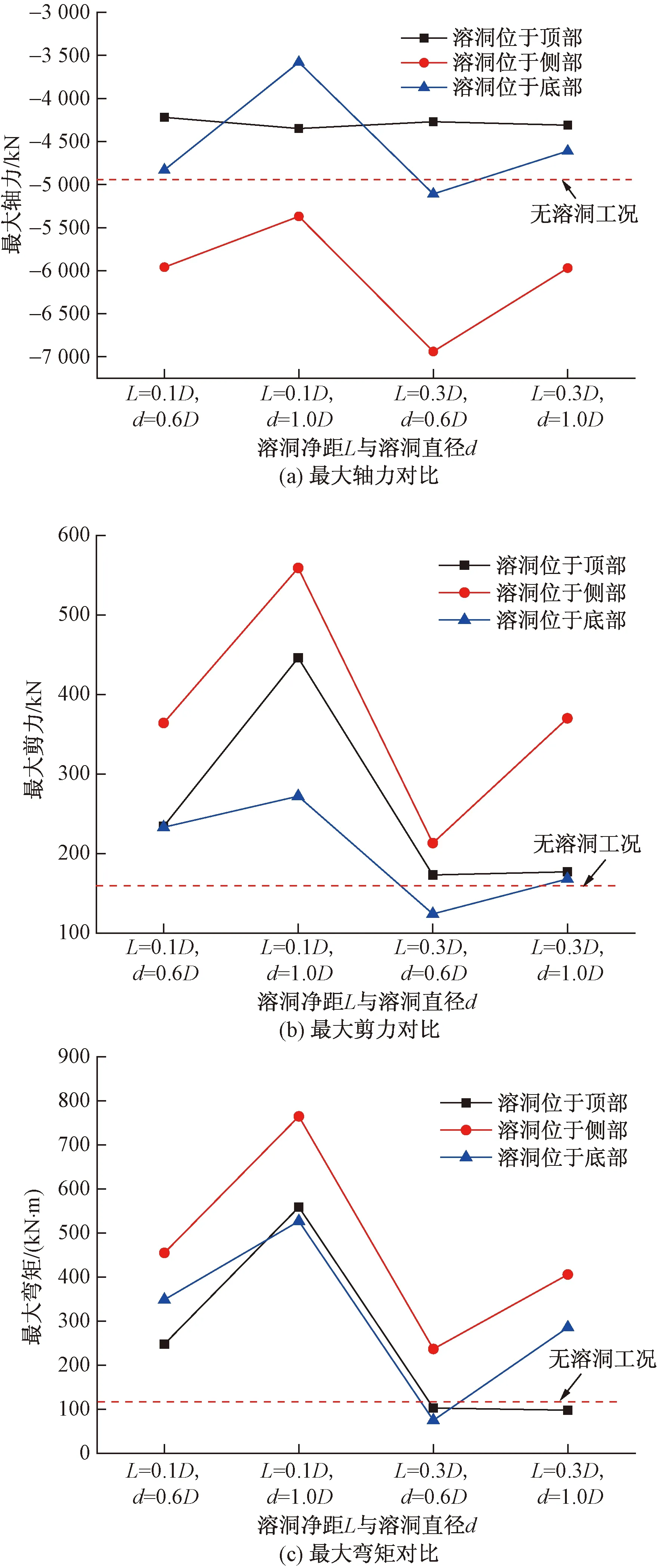
图9 结构内力对比变化曲线 Fig.9 Structural internal force comparison curve
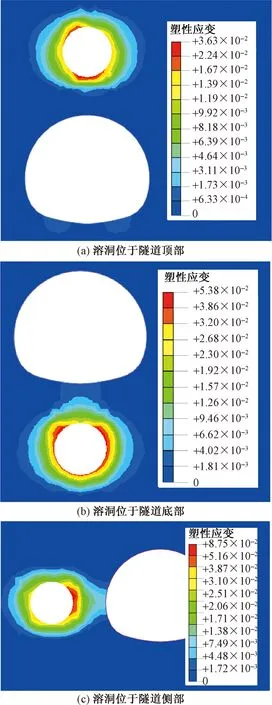
图10 塑性区对比(d=0.4D,L=0.3D)Fig.10 Plastic zone cloud map comparison(d=0.4D,L=0.3D)
3 结论
综合考虑溶洞分布位置、尺寸大小以及与隧道净距等不同因素,开展了溶洞对隧道结构变形与受力影响的数值模拟研究,得出以下结论。
(1)溶洞使隧道结构变形与受力发生改变,随溶洞与隧道间净距增大,隧道结构的位移逐渐较小,在同一净距下,随溶洞尺寸增大隧道结构位移增大,反之则相反。此外,隧道结构在靠近溶洞一侧变形与内力均较大,易产生应力集中现象。
(2)当溶洞直径d≤0.4D时,溶洞对隧道结构影响较弱,当溶洞直径d≥0.6D,且与隧道净距L≤0.3D时,溶洞对隧道结构变形与内力均影响显著,为施工危险区,故隧道在此区域施工时,应采取有效的超前加固措施,同时加强围岩与支护结构的监控量测,以科学指导施工。
(3)对比分析得出对隧道稳定性最不利的溶洞位置是隧道侧部溶洞,溶洞位于隧道顶部和底部时,影响相对较弱。
需要指出的是文中仅进行了溶洞分布位置与尺寸大小对隧道结构影响的数值模拟,探讨了溶洞空腔对隧道结构变形受力的影响,而溶腔充水以及施工时突水突泥对隧道结构的影响尚需进一步深入研究。

