距离与权重相结合的导向式灰盒模糊测试方法

李明磊，陆余良，黄 晖，朱凯龙

（国防科技大学电子对抗学院，合肥 230037）

0 概述

随着社会信息化程度的不断提高，网络空间安全成为国家安全的重中之重。在威胁网络空间安全的众多因素中，漏洞是最根本的原因。模糊测试技术是目前最有效的漏洞检测技术之一，其为被测程序提供多种输入并监测被测程序的多种异常行为，如堆栈或缓冲区溢出、内存泄漏等［1-2］。安全人员通过对程序异常行为进行分析，从而实现对软件漏洞位置定位。

1988 年，MILLER 等人提出模糊测试的概念［3］，经过三十多年的发展，已经形成包括白盒模糊测试、灰盒模糊测试、黑盒模糊测试在内的三类模糊测试技术。白盒模糊测试技术基于程序源代码进行分析，能够根据程序源码提供更具有针对性的测试用例，但对程序的分析会引入大量的额外开销［4］。与白盒测试相反，黑盒测试不对被测程序进行分析，而是仅提供持续不断的输入并对程序运行结果进行收集。这使得黑盒测试具有较好的时间效率，能够在短时间内覆盖程序的大量路径，但不具有针对性的测试用例也使得黑盒测试难以覆盖程序深处的路径。灰盒模糊测试是一种结合黑盒与白盒测试特点的测试方法，模糊测试器在提供给程序大量测试用例的同时通过轻量级程序分析工具对程序运行状态进行分析，并根据分析结果对测试用例进行修改。灰盒模糊测试能够在保持黑盒模糊测试高效、扩展性好的基础上获得对程序关键结构信息分析的能力，使模糊测试技术更加智能［5］。

近年来，研究人员将污点分析［6］、符号执行［7］以及静态分析［8］等技术与灰盒模糊测试技术相结合，使得灰盒模糊测试技术在路径覆盖率、时间效率以及路径覆盖深度等方面取得突破。文献［9］开发的模糊测试器TaintScope 使用了符号执行与污点分析技术，自动标记输入中的校验和字段并求解出可以通过程序校验和检测的测试用例。文献［10］开发的模糊测试器Dowser 使用污点分析技术计算种子文件各比特位之间的突变比例，提高种子文件变异效率。文献［11］开发的模糊测试器BORG 使用静态分析技术得到程序的控制流程图，并利用该程序流程图使用符号执行技术生成可以到达程序高危漏洞的测试用例。文献［12］开发的模糊测试器AflFast 使用马尔科夫链模型对程序路径状态转换概率进行建模，根据概率模型选择覆盖低概率路径的种子进行变异，以提高新路径的发现速度。文献［13］开发的模糊测试器Skyfire 使用概率上下文相关语法从大量现有样本中生成高质量样本。文献［14］开发的模糊测试器VUzzer 使用了静态分析与动态污点分析技术，计算每个种子的适应度来提高模糊测试器路径覆盖的深度。

随着程序规模的不断增长，为提高模糊测试的效率，在进行模糊测试前，研究人员通常会对目标程序进行脆弱性分析等工作，选定程序中存在潜在问题的区域作为目标区域进行测试，如程序的补丁区域。但上述的模糊测试器是面向整个程序进行测试，被用于补丁测试、高危区域测试时缺乏导向性，会将大量时间和系统资源浪费在程序的无关区域。因此，文献［15］提出导向式灰盒模糊测试技术，导向式灰盒模糊测试技术能够快速生成到达程序目标区域的测试用例并发现漏洞［16］，其不需要重量级的符号执行、程序分析和约束求解技术，而是先通过静态分析计算出程序各基本块到目标区域的距离，并通过插桩的方式将距离信息插入到目标程序中，在测试阶段根据插桩信息计算每个种子距离目标区域的距离，使用启发式算法提升距离目标区域近的种子生成测试用例的数量，保证了测试的高效性与导向性［17］。

本文对现有的导向式灰盒模糊测试方法进行分析，提出一种距离与权重相结合的导向式灰盒模糊测试方法，通过改进距离计算方法提高导向式灰盒模糊测试的准确性。

1 导向式灰盒模糊测试分析

本文以文献［15］开发的导向式灰盒模糊测试器Aflgo 为例，对导向式灰盒模糊测试的基本工作流程进行介绍。导向式灰盒模糊测试器由静态分析与灰盒测试两部分组成，静态分析部分仅在模糊测试开始前运行一次，整体架构如图1 所示。

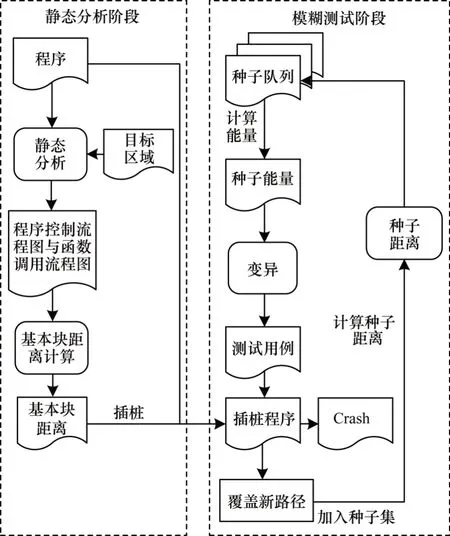
图1 导向式模糊测试技术框架Fig.1 Framework of guided fuzzing test technology

导向式灰盒模糊测试流程如下：

1）在静态分析阶段，对目标程序进行静态分析得到目标程序的函数调用流程图和程序控制流程图。

2）计算出程序每一个基本块到目标区域的距离并通过插桩的方式将距离信息插入到程序中。

3）模糊测试阶段，从种子集中选择一个种子进行测试，收集该种子执行轨迹并计算种子与目标区域的距离。

4）根据种子到目标区域的距离动态调控种子的能量，即种子变异产生的测试用例的数量。

5）如果变异生成的测试用例覆盖到程序新的路径，就将此测试用例加入种子集。

重复操作流程3）～流程5），当种子集中种子都被选择过一遍时为一轮，一轮测试后从种子集第一个种子开始新一轮测试直到时间结束。

Aflgo 通过与Afl 及导向式符号执行工具KATCH［16］进行对比实验，证明了其导向的有效性，但依然存在以下3 个问题：

1）距离计算粒度粗糙，没有仔细区分函数与基本块对种子距离的影响，而是简单地认为函数距离是基本块距离的常数倍。

2）没有对程序不同位置的基本块进行区分，认为程序中基本块的权重是相同的，降低了距离计算的精度。

3）种子能量调控策略以程序运行时间作为调控指标不够准确。程序受运行环境影响较大，同一个程序在不同运行环境下运行相同的时间运行状态有很大的差别。

为解决上述问题，本文提出一种更加精确有效的距离计算与能量调控方法，对图1 中的基本块距离计算与种子能量计算进行改进，以提高导向式模糊测试器的导向性。

2 本文方法

实现导向式灰盒模糊测试导向性的关键在于计算种子到目标区域的距离。通过上文的分析可以看出，目前限制距离计算准确性的主要原因有两点：1）如何计算不同函数、不同基本块对种子到目标区域距离的影响；2）如何用统一的量纲表示程序中函数和基本块到目标区域的距离。本文通过对导向式灰盒模糊测试中的距离与能量计算方法进行改进，将不同函数与基本块的差异考虑到距离计算当中，统一函数与基本块的距离计算标准，设计合理的种子能量调控策略。

为提高距离计算的准确性与合理性，本文将距离计算与能量调控分为函数路径长度（Pf）计算、基本块距离计算、种子距离与能量计算3 个部分。3 个部分为递进关系，计算过程如图2 所示。函数路径长度表示不同函数参与距离计算时贡献的距离，基本块距离指程序中基本块到目标区域的距离，种子距离指进行模糊测试过程中种子执行轨迹到目标区域的距离，本文中目标区域由若干同属一个函数的基本块构成。

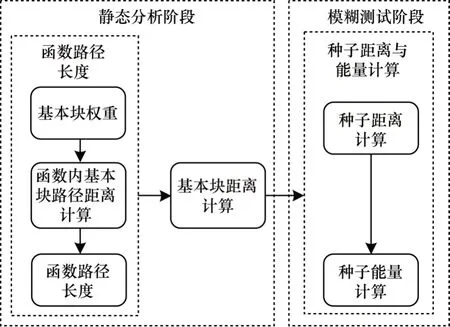
图2 距离计算示意图Fig.2 Schematic diagram of distance calculation

在静态分析阶段完成程序函数路径长度计算与基本块距离计算并将基本块距离插桩到程序中。在模糊测试阶段，模糊测试器记录种子覆盖到的基本块信息，并根据基本块信息计算种子距离与能量。

在计算函数路径长度（Pf）前引入基本块权重（Wb）概念以提高距离计算的合理性。基本块权重表示基本块在程序路径中的重要程度，以区分不同基本块对距离计算的影响。根据Wb得到函数内部基本块间路径距离计算公式L（i，j），路径距离指两点间最短的一条路径的长度。根据本文的方法利用L（i，j）计算程序中每一个函数的函数路径长度，L（i，j）由基本块间的距离而来，因此函数路径长度的量纲与基本块距离的量纲是统一的。

得到程序函数路径长度后，根据公式L（i，j）与函数调用图可以得到程序任意基本块到目标区域的距离。程序基本块距离计算较为复杂，因此将基本块分为四类进行计算，将计算得到的基本块距离插桩到目标程序中。得到包含插桩信息的程序后，根据模糊测试时种子覆盖到的基本块中包含的基本块距离信息计算种子距离并归一化处理。为了更加合理地对种子能量进行调度，根据种子执行轮次对种子能量进行修正。

3 技术实现

3.1 函数路径长度计算

导向式灰盒模糊测试是为了在有限的时间里尽可能多地发现覆盖目标区域的路径。传统的距离计算方法没有对处于程序路径不同位置的基本块进行区分。以图3 所示的程序路径为例，传统的计算方法［15］认为基本块D和基本块B到达目标区域G的距离相同。但从路径图可以看出，经过基本块B到目标区域G有两条路径，而经过D到目标区域G的路径仅有一条，经过基本块B比经过基本块D更容易到达目标区域。传统的计算方式不能体现出不同位置基本块的区别，降低了导向的精度和速度。为提高距离计算的准确性，本文对传统的计算方法进行改进，给不同位置的基本块赋予不同的权重，使得经过B到目标区域G的距离小于经过D到G的距离。

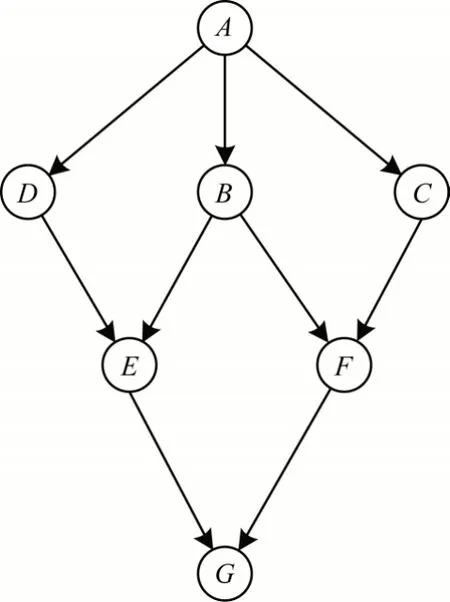
图3 程序路径示意图Fig.3 Schematic diagram of program path

通过对程序路径的分析，一个基本块的后继基本块越多，则经过该基本块的种子变异后覆盖不同路径的概率越高。因此，在距离计算中用基本块出度（一个基本块的后继基本块个数）作为基本块的权重，用符号Wb表示。

在引入基本块权重后基本块间的距离如图4 所示。分别计算图4 中A到G的路径1｛A，D，E，G｝和路径2｛A、B、E、G｝的长度，得到路径1 长度为7/3，路径2 长度为11/6。在未将权重引入前，距离相同的两条路径在引入基本块权重后距离产生差值，经过权重高的基本块的路径距离更短，在变异时可以得到更多的变异机会。

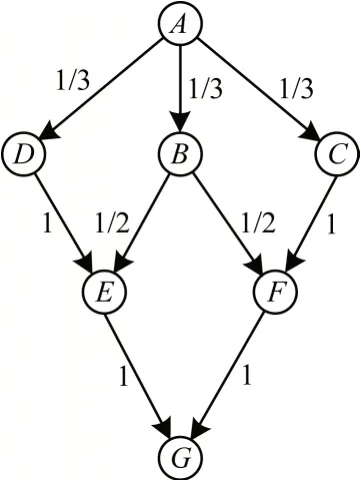
图4 加权路径距离计算Fig.4 Distance calculation of weighted path

式（1）表示同属一个函数的基本块i与基本块j之间的距离，如果从i到j有多条路径则选择其中最短的一条路径计算，集合B表示该路径覆盖到的基本块，i∈B，j∉B。

以图4 为例，A到G的路径有4 条。选择其中最短的一条利用式（1）计算，可得A到G的路径距离L（A，G）=11/6。

在之前的距离导向启发式计算规则中［15］，不同函数在基本块距离计算中贡献的距离为相同的常数值，没有考虑到不同函数对基本块距离不同的影响，计算基本块距离时会引起较大的误差。为提高距离计算的精度，本文引入函数路径长度的概念，用函数包含的基本块表示该函数在基本块距离计算中贡献的距离。函数路径长度指一条路径穿过该函数实际经过的距离，用函数入口基本块到函数出口基本块全部路径的距离的平均值表示该长度。

以图5 为例，基本块A为函数入口基本块，基本块G为函数出口基本块。由A出发到G的路径有4 条，分别为｛A，D，E，G｝、｛A，B，E，G｝、｛A，B，G｝和｛A，C，G｝，长度分别为7/3、11/6、5/6 和4/3，因此该函数路径长度为19/12，当该函数参与到距离计算时贡献的距离为19/12。

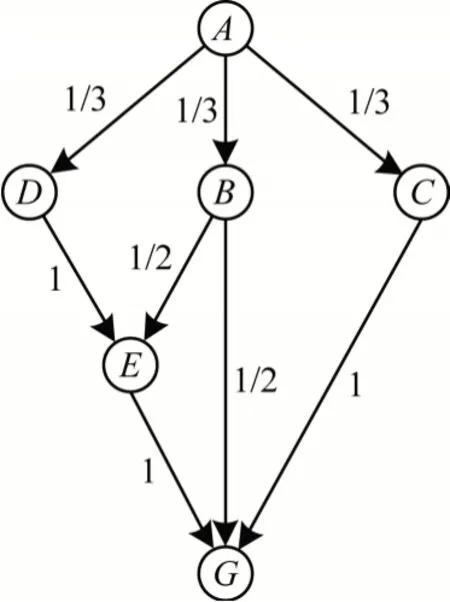
图5 函数路径长度计算Fig.5 Length calculation of function path

3.2 基本块距离计算

依据3.1 节中得到的同属一个函数的2 个基本块间距离计算公式L（i，j）与函数路径长度（Pf）计算方法，计算程序基本块到目标区域距离。依据程序中基本块与目标区域的位置分为4 种情况讨论，如图6 所示。其中，方框表示函数，圆圈表示基本块，三角形表示目标基本块。

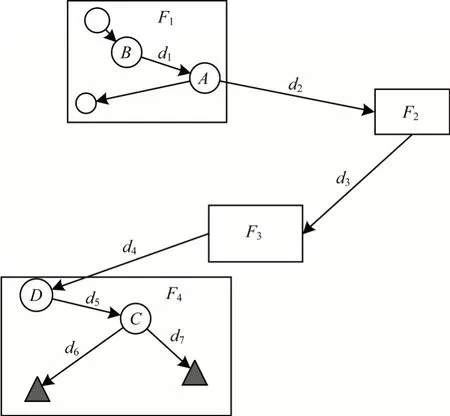
图6 基本块分类Fig.6 Classification of basic blocks

为便于计算与讨论，首先引入符号H，H表示程序中包含目标区域的函数从入口基本块到目标区域的距离。如图6 中基本块D到目标区域的距离，利用式（2）可以求得该距离。集合Bt由该函数包含的目标基本块组成，b1st为入口基本块。

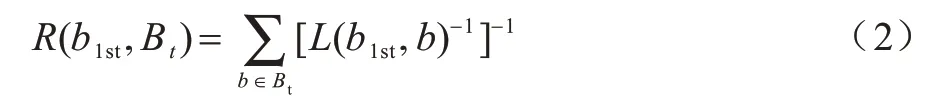
4 种情况讨论如下：

情况1当基本块为目标基本块时，该基本块到目标区域的距离为0。

情况2当基本块与目标区域属于同一函数但不是目标基本块时，如图6 中的基本块C。利用式（1）分别计算基本块C到每个目标基本块的距离后，求调和平均值作为基本块C到目标区域的距离。

情况3当基本块与目标区域属于不同函数但可以直接通过函数调用到达目标区域所在函数时，如图6 中基本块A。用基本块A调用的系列函数的函数路径长度的倒数和加上H作为基本块A到目标区域的距离，即图6 中函数F2与F3的函数路径长度的倒数和与函数F4的H之和，如果有多条调用路径则取平均值作为该基本块的基本块距离。

情况4当基本块与目标区域属于不同函数且可以通过同属一个函数内的其他基本块到达目标区域所在函数时，如图6 中基本块B通过基本块A可以到达包含目标区域的函数F4。计算出基本块A到目标区域的距离，在用该距离加上基本块A到基本块B的距离，作为基本块B到目标区域的距离。

式（3）为基本块距离计算公式，集合Tb由目标基本块组成，集合Ta由与目标基本块同属一个函数的基本块组成，集合Tf由可以直接到达包含目标区域的函数的基本块组成，集合Tj由可以通过Tf中的元素到达包含目标区域的函数的基本块组成。集合Fi由基本块i到包含目标区域的函数所需要调用的函数组成，Num（Fi）表示集合Fi中元素的数量，Pf表示函数f的函数路径长度。

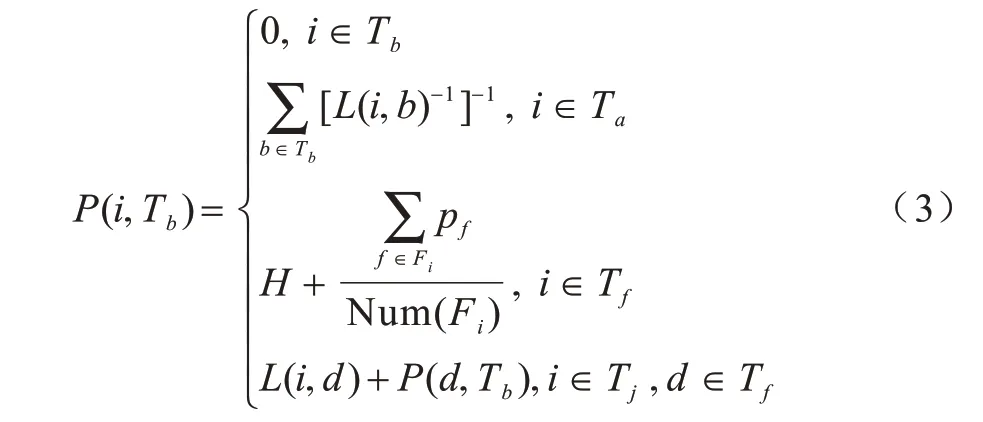
在静态分析阶段利用式（3）完成对基本块距离的计算，计算过程如算法1 所示。

算法1基本块距离计算算法

对算法1 的代价进行分析，假设程序有m个函数和n个基本块，符号Ki表示函数i包含的基本块数量。对算法中第一个双层循环进行分析（算法第1行～第6 行），由函数路径长度计算方法可知，Calculate_Pf（function）相当于对函数function 包含的基本块进行一次遍历，代价为O（kfunction），而第二层循环（算法第2 行～第5 行）代价也为O（kfunction），所以算法1 中第一个双层循环总执行次数相当于程序中每个函数包含的基本块数量之和的两倍，故代价为O（n）。对算法1 第二个双层循环（第9 行～第11 行）进行分析，由式（3）可知Calculate（BB）的代价为O（m），故第二个双层循环的代价为O（m×n）。取两个双层循环代价之和作为算法1 的总代价，总代价为O（（m+1）×n）。多数应用程序中基本块数量远远大于函数数量，m+1 可以看为常数项，所以距离计算花费的代价为O（n）。

3.3 种子距离与能量计算

在3.2 节中得到了程序中任意基本块到目标区域的距离计算公式。在对程序静态分析时利用公式计算出每一个基本块到目标区域的距离并插桩到程序中。在模糊测试时追踪每个种子执行的轨迹，根据种子执行到的基本块计算该种子到目标区域的距离，如式（4）所示：

其中，集合Q由种子s覆盖的基本块构成，Num（Q）表示集合Q内元素的数量。

对种子距离进行归一化得到式（5），集合S由模糊测试器使用的种子构成：

在模糊测试中种子能量是用来调控一个种子变异次数的重要变量，如果一个种子与模糊测试器的测试策略契合度越高，那么该种子得到的能量也越高，在种子进行变异时模糊测试器会根据种子的能量对种子进行变异操作，种子能量越高变异生成的测试用例越多。

为避免种子在模糊测试一开始就收敛到某一条路径上，将模糊测试执行的轮次t作为调节种子能量的因子。使得模糊测试在初始的几轮测试中能够探索足够多的路径，避免模糊测试路径过度集中。将Afl 能量计算方法［18］与式（7）结合可以得到种子能量计算公式：

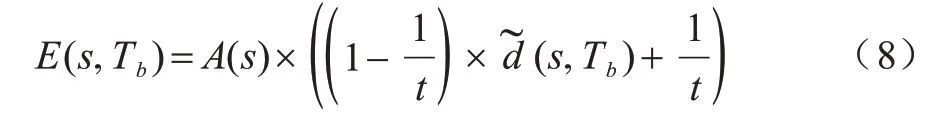
其中，A（s）表示在Afl 能量计算中种子s的能量。

当t趋近正无穷时，E(s，Tb)=A(s)×(s，Tb)；当t=1 时，E(s，Tb)=A(s)。当模糊测试刚开始时种子的距离对能量计算不会产生影响，而随着迭代次数的增加，种子距离对能量的影响逐渐增强。图7 为不同迭代次数对种子能量变化的影响，可以看到当种子距离一定时，随着迭代次数的增加，种子能量在初始的几轮迭代中急剧变化后迅速趋于稳定，这证明了迭代次数t仅在测试开始阶段影响种子能量计算，随着迭代次数的不断增加，t对种子能量影响逐渐降低，种子距离在种子能量计算中起主导作用。

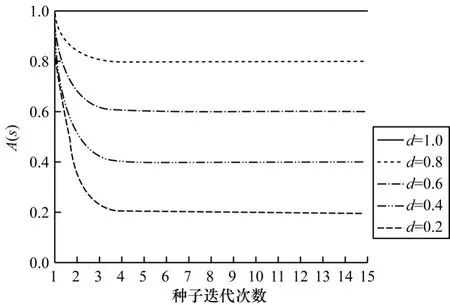
图7 迭代次数对种子能量的影响Fig.7 Effect of iteration times on seed energy

4 实验与评估

为验证本文方法的有效性，基于Afl［18］设计实现了原型系统Afl-guide，并与Aflgo、Afl 进行对比实验。Afl-guide 使用LLVM［19］对目标程序进行分析生成函数调用图和函数控制流程图，使用Python 脚本利用Networkx 包实现对函数调用图和函数控制流程图的解析并计算基本块距离。扩展Afl 的插桩模块，将基本块距离插桩到程序中。

本文结合Aflgo，选取libming 与GNU Binutils 作为测试程序。libming 是一款使用C 语言编写的Flash（SWF）输出库，可在C ++、PHP、Python、Ruby和Perl 中使用，拥有10 万行的代码，是被广泛使用的开源项目。GNU Binutils 是GNU/Linux 平台中使用的二进制分析工具集，有着近100 万行的代码，被广泛用于对模糊测试工具的测试中［20-21］。

实验选取libming 和GNU Binutils 中近年公开的CVE 作为导向目标，分别用3 个工具对目标程序进行实验，每组实验重复5 次，持续24 h。实验结果如表1 和表2 所示，其中，Arrive 表示到达目标点的次数，TTE 表示第一次覆盖到目标站点花费的时间，Improve 为改善因子，值为Afl-guide 的TTE 与Aflgo和Afl 的TTE 的商，表示相较于Afl 与Aflgo，Aflguide 的效率提升了多少。实验服务器设置为：AMD ryzen7 2700 处理器，64 GB 内存，2 TB 固态硬盘，运行Ubuntu 16.04（64 bit）操作系统。

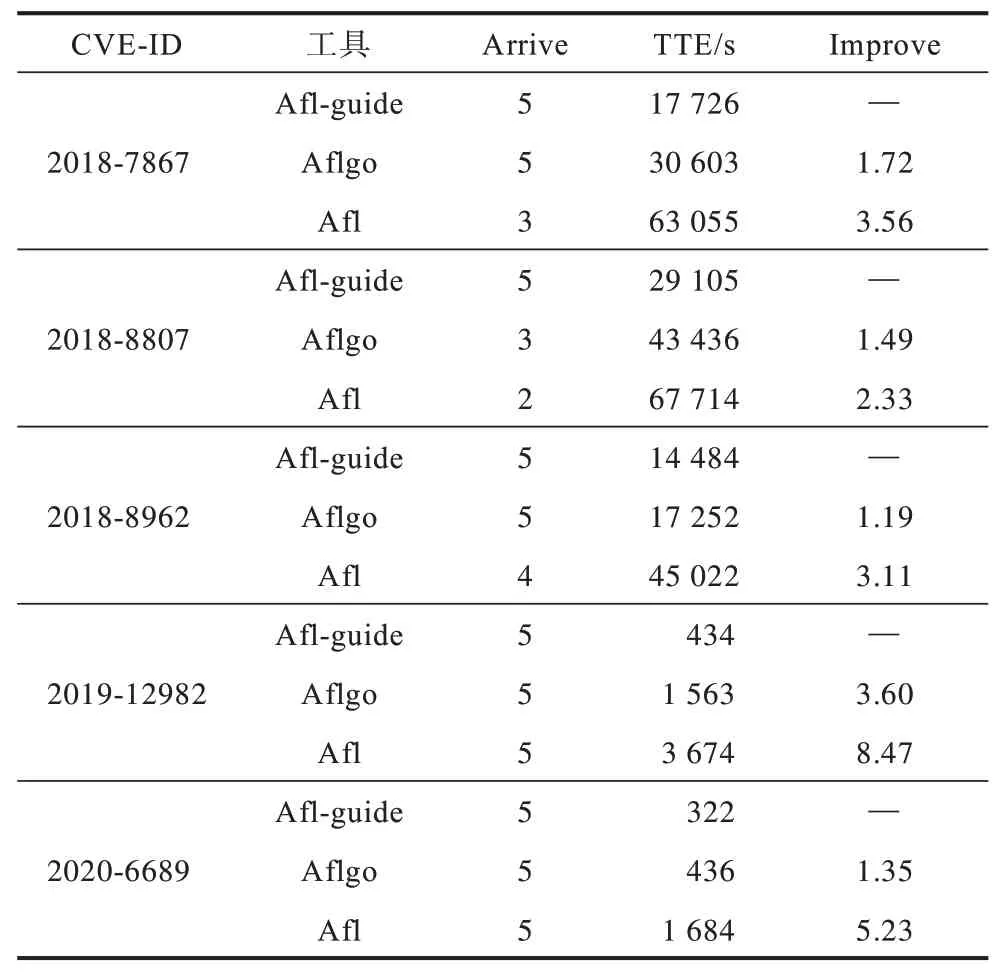
表1 libming 目标站点覆盖Table 1 libming target site coverage

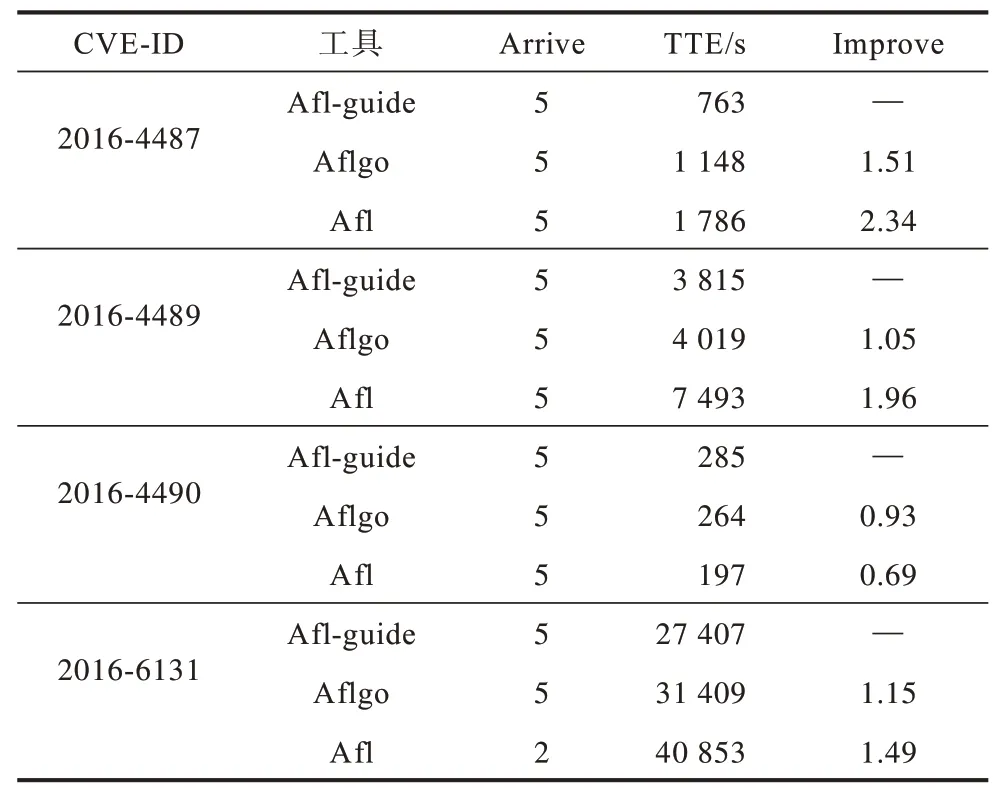
表2 GNU Binutils 目标站点覆盖Table 2 GNU Binutils target site coverage

在表1、表2 的数据中，除CVE-2016-4490 外，Afl-guide 与Aflgo 到达目标区域的时间明显小于Afl，证明了Afl-guide 与Aflgo 的导向性。在CVE-2016-4490 中，目标站点在程序路径的浅层容易被测试用例覆盖，因此导向式模糊测试器在测试的过程中引入的资源消耗反而导致Afl-guide 与Aflgo 覆盖目标站点的速度慢于Afl。通过表1 和表2 中的数据还可以看出，利用本文方法实现的工具Afl-guide 在导向性上优于Aflgo。在CVE-2018-7867 中提升最为显著，Afl-guide 到达目标点仅用了Aflgo 花费时间的27.8%。实验结果表明，使用本文的方法可以快速生成覆盖程序指定位置的测试用例，能够大幅提高在已知程序脆弱区域、补丁检测等情景下的模糊测试效率。

为进一步说明在种子能量计算过程中引入种子迭代次数的对路径收敛速度的影响。Aflgo 与Aflguide 路径覆盖率比对情况如表3、表4 所示。其中，Cov 表示第一次覆盖到目标区域时模糊测试器的路径覆盖率。AveC 表示Cov 与TTE 的比值，Better 值为Aflgo 的AveC 与Afl-guide 的AveC 的商，表示相较于Aflgo 的覆盖率提升了多少。

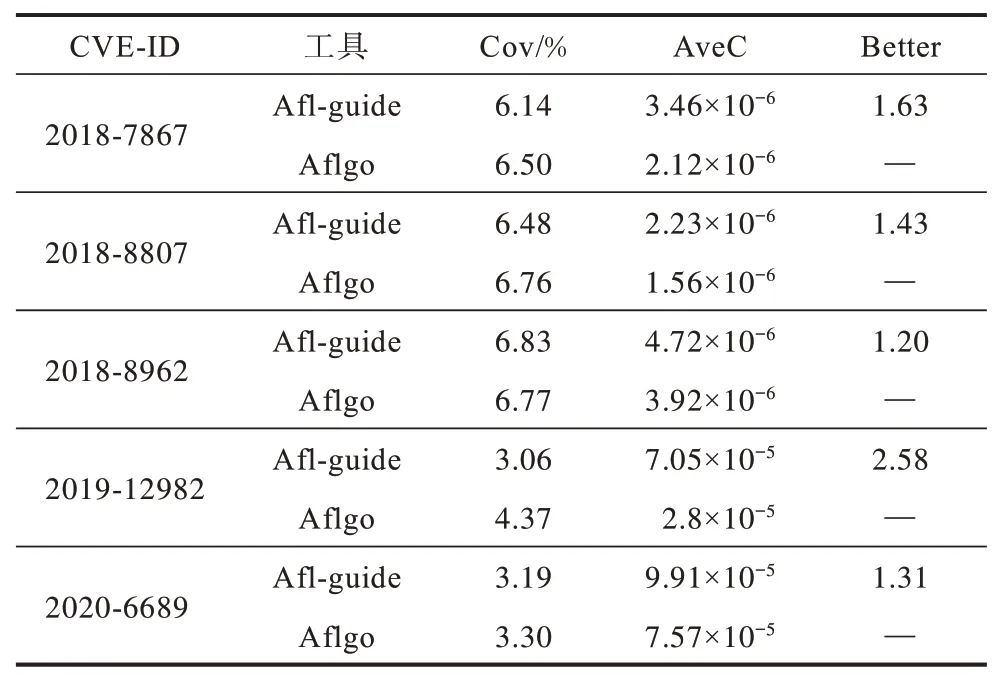
表3 libming 路径覆盖率Table 3 libming path coverage

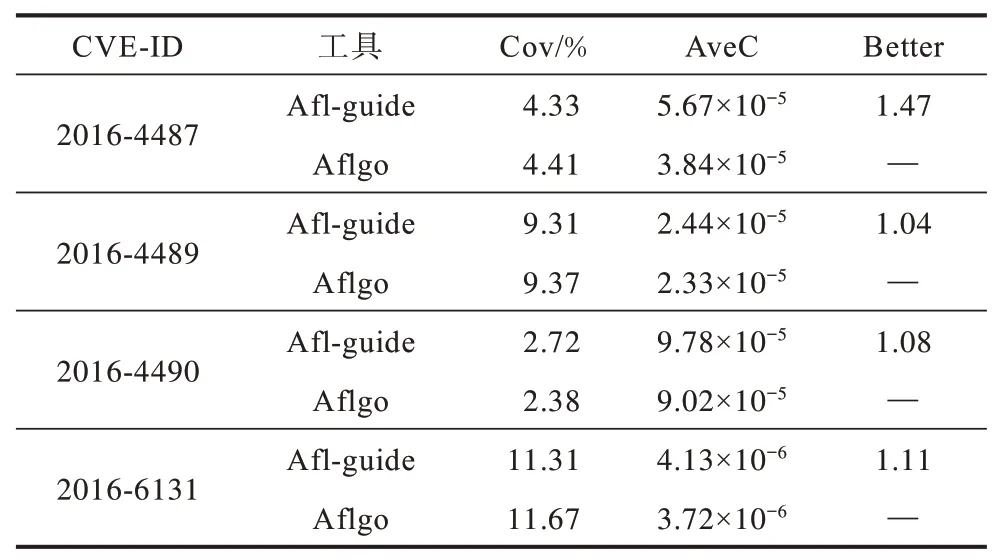
表4 GNU Binutils 路径覆盖率Table 4 GNU Binutils path coverage

从表3、表4 可以看出，Afl-guide 与Aflgo 在到达目标位置时路径覆盖率基本一致，但考虑到所花费的时间，单位时间内Afl-guide 的路径覆盖要高于Aflgo。证明在种子能量计算中引入种子迭代次数达到了预期的目标，在测试初期快速探索路径并随着轮次的增加快速收敛到目标区域。

5 结束语

本文对导向式灰盒模糊测试进行研究，提出一种距离与权重相结合的导向式灰盒模糊测试方法。对距离计算方法进行改进，提高了距离计算的精确性，增强模糊测试器的导向性。实验结果表明，该方法能够有效提高模糊测试导向的效率以及对目标区域覆盖的概率。由于现在的静态分析工具还无法有效识别程序中的间接调用，导致函数距离计算中存在一定的误差，同时程序中存在校验和的情况使得种子无法覆盖到目标区域。下一步将对静态分析方法进行改进，以提高函数距离的精度，并将符号执行与模糊测试相结合，使模糊测试可以对校验和程序进行快速导向。