连续语义学及其分析量词位置和辖域问题的尝试

石运宝，邹崇理

(湘潭大学 碧泉书院·哲学与历史文化学院，湖南 湘潭 411105)

一、连续(Continuation)概念介绍

通俗来讲，“连续”是指执行程序的过程中连续应用函数(applying functions)的操作，使得每个函数输入在前的函数输出的结果。举例来说，存在两个函数的复合，如f和g，g输入整数n，得到函数值g(n)，得到的结果作为论元输入到函数f中，结果是f(g(n))。这里g被应用于函数f，g的连续在于将g作为论元输入的那些函数，f是其中之一。

我们可以换个角度看待“连续”。拿上面的例子来说，通常的程序语言这样理解：f为g(n)提供了一个语境(context)(1)由于“连续”始终缺乏一个符合直观的解释，所以下文用表达式的“语境”、函数的“未来”等近似表达“连续”的涵义。：

语境：f[ ]

项： g(n)

其中，项要输入到语境中去计算出某个值，语境可以表示为一个λ-项：λx.f[x]，而项g(n)则作为论元输入到λx.f[x]中。Alain Lecomte[12]设想了一个问题可以解释“连续”概念在程序语言中的作用。在运行程序过程中，由于某个原因，必须转向另外一个函数。此时，改变函数有两种办法：一种是调整原来的函数；一种是将提升论元作为函数，把原来的函数作为论元。

就第二种方法而言，需要结合g寻找一个新函数g′，满足：

g′(n)(λx.f[x])=λx.f[x]( g (n))

这时，之前的语境变成了运算对象，之前的项转换成新的语境(2)注意，一般来说g与 g′不同，这里用的是转换，即二者相关，但并非与之前的语境直接调换位置。。这样做的好处是，如果我们想改变程序的“未来”，即连续，那么可以结合之前的项(论元)创造一个新函数。使用“连续”概念的程序被称为“连续传递风格”(continuation passing style,CPS)。已有自动的技术将正常的程序或某个语法转换成CPS。

Kelsey等[5]认为，“连续”表征了适用于计算的全部的(预先设置好的)未来(a continuation represents the entire (default) future for the computation)。从语言学角度来说，若给定一个句子“John admires Mary”，为了计算该句子的意义，主语John所指称的值的“默认未来”是指，拥有“admiring Mary”这一性质。形式上来说，主语John的指称j的未来是函数λx.(admires m) x；类似地，宾语Mary的指称m的默认未来是“being admired by John”这一性质(所确定的集合)，形式刻画为函数λy.(admires y) j；动词admire的指称是函数λR.R m j，故动词短语admires Mary的连续是函数λP.P j。拿“admiring Mary”这一性质来说，凡是拥有这一性质的个体都可以作为论元输入，所以这一性质刻画了一个集合，相当于John的择代集(alternative-set)(3)择代集概念由Rooth[13]最早提出，用于解决强调部分的语义，John introduced[Bill]F to Sue.表示语气上强调“Bill”，则该表达式的语义为<λx[ introduce (j,x,s)],b>，其中被强调的部分Bill有两个值，一个是通常的指称，即b，还有一个强调语义值(focus semantics value)，即λx[ introduce (j,x,s)]函数所表达的性质“John introduced x to Sue”，该“强调语义值”由一个择代集组成。，就“John admires Mary”而言，John的连续已由该语境预先设置好(default)，所以对于某个表达式而言其连续可以看作某个语境中预先确定好的未来所有可以替代该表达式进行输入的那些对象所组成的集合。

通过这个例子，可以得出两点启发，一是(句子中)每个有意义的子表达式(subexpression)都有一个连续，二是每个表达式的连续总是相对于某个比它更大的表达式来说的。就第二点来说，当John出现在句子“John left yesterday”中时，John的指称j的连续是λx.yesterday left x这一函数所表达的性质；在句子“Mary thought John left”中，John的指称j的连续是λx.thought(left x)m这一函数所表达的性质；而在句子“Mary or John left”中，John的指称j的连续是λx.(left m)∨(left x)。

值得一提的是，连续语义学有比较广泛的应用性。Barker[7]将连续语义学应用于自然语言处理，该尝试很好地阐释了连续在程序和形式语义学领域的应用。应用连续语义学的动机之一，是可以为量词辖域歧义问题提供很好的解决方案，克服之前文献中缺乏一致性等疑难(比如主项和谓项未做到统一处理等不足)。

二、为某个语法提供连续语义学

首先，给出一个简单的语境自由语法(context free grammar)，如图1所示：

如图2所示，每个语义对象(方括号中间的部分)都具有固定的类型(4)给定一个语言单位，将其置于[[.]]之中，它对应的类型放到右边，基本思路是，左边的属于句法范畴或属于该范畴的某个句法单元，右边的属于语义类型或该类型的载体(或者说刻画左边范畴的语义标签)。：

其中，S是句子的范畴，t表示s的类型为真值。举例来说，句子“some boy walks”，其中some为限定词，其范畴为Det，类型为(e → t) → ((e → t) →t)；boy范畴为N，对应的类型为(e → t)，some和boy通过函数应用后得到的短语some boy的类型为((e → t)→t)，而walks对应的范畴为VP，类型为(e → t)，some boy和walks进行函数应用，即将类型为(e → t)的论元输入到类型为((e → t)→t)的函数中，得到类型为t的“some boy walks”，即其类型指向真值。

如果要为某个语法提供连续语义学，不只是要为每个表达式找到其连续，还要提升该表达式的类型，使其成为以其连续为论元的函数(5)直观上，提升John的类型，使其成为saw Mary的函数，可以理解为John指称的个体具有saw Mary这一性质，即提升后的John是这样一个函数，需要输入saw Mary这一性质才形成一个完整的句子。。比如，上述涉及的专名、谓词、通名的连续语义(上标c表示连续语义)为图3：

图3 表达式对应的连续语义

由此可知，不仅专名(上述名词短语NP)获得了类型提升，其余短语也获得了类型提升，故类型提升操作变成了一个规则。

图3提供了如何将单个表达式转换为连续语义的规则，而仍待解决的问题是，当一个λ项被应用到另外一个λ项时如何通过CPS方式进行转换。

令M和N是两个λ项，类型分别是α → β和α，通过CPS转换后分别为Mc和Nc，类型分别是((α → β) → t) → t和 (α → t) → t。如果将M应用到N，即(M N)，可以视为N被置于语境M[]中，(M N)被置于空语境[ ]中。按照连续语义学的思路，整个语法都连续化了，因此，(M N)的连续语义应该将N的连续语义作用于M的连续语义，即(M N)的连续语义为：Nc(Mc[ ])。

(M N)的类型为β，(M N)的连续的类型β→ t，所以Nc(Mc[ ])，即(M N)c的类型应该是(β →t) → t)。但现在的问题是如何证明由类型为((α → β) → t) → t 的Mc和类型为 (α → t) → t的Nc可以推出类型为(β → t) → t的(M N)c。图4给出了自然演绎式的证明：

图4 (M N)c类型的自然演绎式的第一种推演

由此可以得出(M N)的连续语义为：

<1> (M N)c=λu.(Mcλm.(Ncλx.(u(mx))))

将该结论应用于John left，可以得出：

将最后一行的结果应用到类型为t → t恒等函数(identity function)λp.p，得：

但图4的推演并不唯一。事实上，还存在另外一种推演，即图5：

图5 (M N)c类型的自然演绎式的第二种推演

因此，(M N)的连续语义存在另外一个形式：

<2> (M N)c=λu.(Ncλx.(Mcλm.(u(mx))))

两种可能性表达了不同的赋值顺序，在式<1>中，M的部分处于宽辖域(例子中的VP的语义部分)，而N(例子中的VP的主语的语义部分)处于窄辖域；在式<2>中则相反，主语部分处于宽辖域，动词短语部分处于窄辖域。虽然赋值顺序对于上述例子John left来说无关紧要，但对于量化短语来说，赋值顺序却是非常重要的。鉴于两种翻译都有效，所以就某个句子来说存在不同的逻辑表征。因此，对于最初的语境自由语法，存在两种不同的翻译：

三、 值传递(call-by-value)和名字传递(call-by-name)

Alain Lecomte[12]介绍了两种赋值的方法，计算科学领域的术语是“call-by-value”和“call-by-name”，从计算的角度来说，主要牵涉到λ-演算中β-化简(6)β-化简对应的英文是β-reduction，对应的运算为：((λx.M)n) → M[x → N]，其中M[x → N]，是指M中的x被替换为N。从外到内还是从内到外的两种不同顺序。比如下面的λ-表达式：

(λx.(λy·(x y)u)z)

可以给出两种β-化简：

第一种是从外到内(“call-by-name”)：

(λx.(λy.(x y)u)z) → (λy·(z y)u) → (z u)

第二种是从内到外(“call-by-value”)：

(λx.(λy.(x y)u)z) → (λx·(z u)z) → (z u)

然而，上述两种化简并非总会得出一致结果。首先，存在特定语境，更偏好于某种赋值或化简；其次，在非汇聚性的系统中，两种赋值方式会导致不同的结果。下面给出的例子会更好地解释上述称呼，即“call-by-name”和“call-by-value”的来源：

(λM.(M u)(λk.λy.(k y)g))

如果按照值传递进行化简，则有：

上述化简先将论元部分，即(λk.λy.(ky)g)，进行化简，计算出其值，然后将该值传递到M中，这就是值传递的思想。这种思路是说，假如想化简(M N)，则是在N赋值之后再进行，不会是未化简就进行二者的函数应用运算。

再看另外一种化简思路：

这种思路是说，先不化简论元，而是整体代入，即将(λk.λy.(k y)g)代入到λM.(M u)中，去替换M，然后继续进行化简。这种思路先不化简论元，而是尽量晚地化简，即尽量晚地给论元赋值，就好像“冻结”整个论元一直到最后才“解冻”，即进行赋值运算。这样，一般性地，在化简(M N)过程中，论元N未被赋值便将其传递给M，这就是名字传递的思想。

针对上述两种化简方式，下面介绍表达式和表达式之间的函数应用所对应的“连续”分别是什么。

在连续语义学中，所有表达式都是以连续形式出现的，一个表达式，如λP.P(j)，在输入某个表达式得连续后，比如λx.left(x)，便可以进行上述两种方式的化简了。这两种化简分别对应不同的连续。

按照值传递化简，一个类型为α → β的函数表达式M，在连续语义学中被解释为这样一个表达式，先输入类型为的α值，再吸收β类型的项的连续(该连续的类型为β→t)(7)在连续语义学中都是使用连续，所以这里要用β-类型的项的连续，但不同的是值传递要求先赋值。，最终输出t，也就是说，按照值传递，一个类型为α → β的函数的连续的类型为：

α → ((β → t) → t)

则该函数M的连续语义为吸纳这种类型的连续生成类型为t的表达式：

在值传递中，类型为α的表达式N的连续的类型为α → t，其连续语义与之前给出的相同：

在值传递中，两个表达式的函数应用(M N)的连续语义为(8)Alain Lecomte[12]给出了值传递式和名字传递式连续语义风格翻译的具体推演过程；下标v和n用于区别值传递和名字传递不同的化简对应的连续语义风格翻译。：

类似地，可以得到，在名字传递中，两个表达式的函数应用(M N)的连续语义为：

由上可知，在值传递中，类型为α → β的表达式被解释为这样一个函数，该函数输入赋过值(类型为α)的表达式，输出某个语境中待赋值的表达式(该表达式本身需要赋类型为β的值，其类型为(β → t) → t，即从类型为β的项的连续到t的函数)。该语义解释的连续化变成这样一个函数，即在某个语境中需要赋类型α → β的值的表达式。所以，在值传递中，类型为α → β的函数的连续语义的类型为：

(α → ((β → t) → t) → t) → t)

在名字传递中，类型为α → β的表达式被解释为这样一个函数，该函数的输入是在某个语境中需要赋类型为α的值的表达式(该值的类型为(α → t) → t，即从类型为α的项的连续到t的函数)，输出是在某个语境中待赋类型为β的值的表达式(该值的类型为(β → t) → t)，即从类型为β的项的连续到t的函数)。该语义解释的连续化变成这样一个函数，即在某个语境中待赋值待赋类型为α → β的值的表达式。因此，在名字传递中，类型为α → β的函数的连续语义的类型为：

(((α → t) → t) → (β → t) → t) → t) → t

可以区分出三类对象：

① 类型为α的值，形成一个集合Vα；

② 类型为α的项的连续，形成一个集合Kα；

③ 演算形式，在某个语境中待赋α-类型的值的表达式，形成一个集合Cα。

在值传递中，类型为α → β的表达式被解释为Vα到Cβ的函数，而在名字传递中，被解释为Cα到Cβ的函数，其中Cα中的元素是从Kα到t的函数。

四、 连续语义用于解决量词位置导致的问题

第二部分给出了构建某个语法连续化的过程，给定连续化过程后，可以用它恰当刻画量化短语的辖域问题。首先给出全称量词和特称量词的连续语义：

从上述刻画中只能看出二者是量化的，并且只能结合连续的表达式才能确定其意义。另外，需要注意的是，名词短语everyone的指称类型与连续的NP(如John、Mary)的指称类型，即从NP的“连续”到真值的函数。量化的NP和其他NP指向同样的语义对象，不同之处在于量化的NP受益于连续所带来的不同赋值顺序。

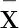
(一) 类型不匹配问题

举例来说，当量化短语在主语位置，如Everyone left，直接赋值得到∀x.left x。一般来说，当量词在宾语位置，如果按照通常的类型分析，量词与名词生成类型为<，t>的表达式，为及物动词指定类型为>的表达式，会造成类型不匹配。这个问题在连续语义学中不会出现，拿“John saw everyone.”来说：

为最后一行的推演添加恒等函数(λp.p)，则：

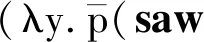
按照连续语义进行分析，不论量化短语出现在主语还是宾语位置，都不会出现类型不匹配的问题。

(二)量词辖域歧义问题

以上对连续语义的分析为一个句子提供了一个合理的分析，但现在的问题是，如果有辖域歧义，该怎么处理。

事实上，在第二部分的结束部分已经粗略给出了思路，连续化语法提供了不只一种方式连续某个组合规则。就S→ NP VP来说，(NP VP)这条组合规则对应两条翻译规则<3>和<4>，如果没有量词出现，两条连续规则推导结果是一样的；如果有量词出现，规则<3>和<4>会导致不同的辖域刻画。

从计算角度来说，规则<3>和<4>对应不同的程序执行顺序。Meyer等[15]指出，程序语言对表达式进行赋值可能会出现差异，差异来源于论元是从左到右被赋值还是从右到左被赋值。如果需要从左到右被赋值，选规则<3>是连续语法正确的选择，反之则选规则<4>。

当然，处理自然语言语义时，规则<3>和<4>都可以使用，结果是导致歧义，这与自然语言量词句本身存在结构歧义的事实相符合。

可以说，规则<3>使得VP优先于NP,所以VP中的量化成分的辖域宽于NP成分；类似地，规则<4>使得NP优先于VP，所以NP中的量化成分的辖域宽于VP成分。如果不添加额外的信息，这两种优先级都有效，所以通过连续语义学，量化表达式的位置问题和辖域歧义问题自动得到解决。

“连续”概念及“连续变元”的引入，促使不同于经典λ-演算的λμ-演算的出现。Parigot[16]给出了λμ-演算系统(9)不同文献记法不一样，有的文献是λμ-演算，而有的文献是λμ-演算。。在λμ-演算系统中，除了正常的λ-变元，还有μ-变元，后者即刻画连续概念的变元。就连续概念，从计算的角度来说，赋值语境的变化相当于从一个指令“跳转到”另外一个，这就假定了不同指令被赋予不同的标签(比如“goto”指令)或者不同的指令被赋予不同的名字。同理，从逻辑的观点看，这相当于某公式被赋予某个名字。当一个项t被命名为α，记为：[α]t。一个被命名的公式在运算中发挥作用(become active)，是通过对该名字进行μ-抽象实现的：μα·e。

在λμ-演算中，为量化表达式指派的语义表征和范畴如下：

有了上述范畴和语义标签，像“everyone loves someone”这样的量化歧义句在λμ-演算中得到如下两种推演(10)这里省略所使用的诸如(β)(μ′)等化简规则的具体内容，详见文献[16]和文献[12]。：

<7> 全称量词宽辖域：

((λx.λy.((love y)x)μα.∃x.((individual x)∧[α]x)),μα.∀x.((individual x) ⟹ [α]x))

→ ((λy.((love y)μα.∃x.(((individual x)[α]x))))(μα.∀x.(((individual x) ⟹ [α]x)))

(β)

→((love(μα.∀x.((individual x) ⟹ [α]x))) μα.∃x.((individual x)∧[α]x))

(β)

→(μβ.∀x.((individual x) ⟹ [β](love x)) μα.∃x.((individual x)∧[α]x))

(μ′)

→μβ.∀x.((individual x) ⟹ ([β](love x)) μα.∃x.((individual x)∧[α]x)))

(μ)

→∀x.((individual x ) ⟹ ((lovex)μα.∃x.((individual x)∧[α]x)))

(σ)

→∀x.((individual x) ⟹ (μα.∃y.((individual y)∧[α]((love x)y))))

(μ′)

→∀x.((individual x) ⟹ (∃y.((individual y)∧((love x)y))))

(σ)

<8> 特称量词宽辖域：

((λx.λy.((love y)x)μα.∃x.((individual x)∧[α]x)),μα.∀x.((individual x) ⟹ [α]x))

→ ((λy.((love y)μα.∃x.((individual x)∧[α]x)))(μα.∀x.((individual x) ⟹ [α]x))

(β)

→((love(μα.∀x.((individual x) ⟹ [α]x))) μα.∃x.((individual x)∧[α]x))

(β)

→(μβ.∀x.((individual x)[β](love x))μα.∃x.((individual x)[α]x))

(μ′)

→μα.∃y.((individual y)∧ [α](μβ.∀x.((individual x)∧[β](love x))y)

(μ′)

→∃y.((individual y )∧ (μα.∀x.((individual x) ⟹ [β](love x))y)

(σ)

→∃y.((individual y)∧(μβ.∀x.((individual x) ⟹ [β]((love x)y))))

(μ)

→∃y.((individual y)∧(∀x.((individual x) ⟹ ((love x),y))))

(σ)

<7>和<8>两种刻画对应上面两种辖域分析，即全称量词宽辖域和特称量词宽辖域。这种解决方案符合蒙塔古(Montague)关于自然语言语义分析的预设：每个非词条的歧义，即不能划归为词条的歧义，应该对应推演的歧义。虽然推演显得繁琐，但内置的“连续”思想可以统一地、组合地、面向表层结构地刻画量化歧义句，这种解决方案具有一阶系统所不具备的生成能力。

Barker[7]给出了连续语义学的其他应用，比如辖域位移(scope displacement)、辖域孤岛(scope island)问题、广义并列现象(generalized coordination)等问题的解析，限于篇幅，这里不多介绍。

五、结语

本文主要介绍了连续概念的涵义、如何“连续化”某个语法，以及连续语义学的语言学运用。“连续”是非常成熟且应用非常广的技术。借助于本文给出的语境自由语法，本文展示了连续语义学可为自然语言处理过程中遇到的诸多难题提供统一的处理方案。由于连续化过程中整体做了类型提升，故无需为特定表达式专门进行类型提升，且为量化表达式提供了在原地(in-situ)的解释，这一点符合当代形式语法和形式语义学界面向表层结构的偏好。不足之处在于，没有为某个有意义的语法，比如为对称范畴语法(Symmetric categorial grammar)提供一个连续语义学示例，这值得后续继续研究。连续语义学之“连续”让人从名字上联想到数学界著名的连续统问题，然而连续概念是否与该问题相关，则有待考察。