侵彻战斗部-引信系统动力学建模与仿真

程祥利， 刘波， 赵慧， 刘军

(中国工程物理研究院 电子工程研究所, 四川 绵阳 621999)

0 引言

以空腔膨胀理论与微分面元法为基础的经验公式广泛应用于侵彻过程理论分析与计算[1-4]，其基本思路是根据质量守恒定律与动量守恒定律建立微面元法向应力与空腔膨胀速度的关系，通过对弹头表面积分得到靶体响应力[5]，并作为衡量侵彻引信受力环境的标准。

但是，上述计算方法假设战斗部为刚体，只能得到刚体过载[6]，与有限元仿真结果、试验测试结果有很大区别，原因是忽略了各种振动的影响，如战斗部振动、引信内部振动，无法真正有效地指导引信等弹载产品的抗高过载优化设计。因此迫切需要一种简单、有效的侵彻战斗部- 引信系统动力学模型，以揭示引信电路模块的动态响应机理。

本文将机械振动理论引入侵彻过程理论分析与计算，提出一种简化的侵彻战斗部- 引信系统动力学模型。首先，简介侵彻战斗部- 引信系统，分析其载荷传递关系；其次，基于多自由度弹簧- 质量- 阻尼系统建立侵彻战斗部- 引信系统动力学模型，并通过谐响应分析确定动力学模型参数；最后，采用数值积分方法预测不同靶体响应力作用下的战斗部、引信响应特性，并与谐响应分析结果、火炮试验结果进行对比，以验证动力学模型的准确性。

1 侵彻战斗部- 引信系统简介

典型的侵彻战斗部[7]由壳体、主装药、传爆序列、后端盖组成，而引信通过螺纹连接[8-9]固定在后端盖上，不与主装药直接接触，如图1所示。

由于螺纹连接刚度比较大，本文近似为刚性固连，不考虑螺纹连接结构的载荷传递特性。另外，引信与主装药并不直接接触，不考虑主装药剧烈振动[10]对引信的影响。

侵彻引信主要由机械壳体、缓冲材料、电路模块等组成。为了确保内部电路模块在数万g载荷作用下不失效，需要进行防护设计。本文从两方面开展防护设计，原理如图2所示：首先是内部灌封加固，将电路部分灌封成一个模块[11-12]，目的是提高电路自身的抗冲击能力；其次是外部缓冲隔离，在引信壳体与灌封成型的电路模块之间填充缓冲材料[13]，目的是利用缓冲材料的低波阻抗特性衰减高频应力波，以减小传递至电路模块的作用力。

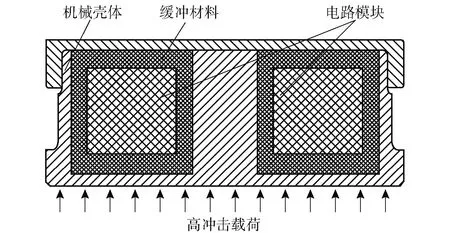
图2 引信防护设计示意图Fig.2 Schematic diagram of protection design for fuze

防护设计完成后，便可得到简化的载荷传递关系，如图3所示。靶体响应力首先作用于战斗部头部，并以应力波的形式沿战斗部壳体传播，随后通过引信机械壳体、引信缓冲材料传递至灌封成型的电路模块。

图3 载荷传递关系Fig.3 Schematic diagram of loading transfer relation

2 动力学模型

从载荷传递关系可以看出，靶体响应力不变时，每一层载荷传递关系的改变都会影响引信电路模块的动态响应特性。如果将侵彻战斗部- 引信系统看作一个动力学系统，则载荷传递关系的改变相当于系统对应的动力学模型发生了变化。

为了简化建模过程，本文主要考虑战斗部轴向振动、引信防护系统的影响，并用电路模块的过载信号来表征引信的动态响应特性。

2.1 侵彻战斗部动力学模型

侵彻过程中，战斗部会发生不同程度的变形，而且拉伸与压缩交替[14-15]。假设变形在线弹性范围内，则战斗部在侵彻过程中主要存在两种运动形态：一是刚体运动，表现为战斗部以一个质点侵彻靶标；二是轴向振动，表现为战斗部尾部(即引信安装位置)以各阶固有频率相对头部振动。

假设战斗部的振动是各阶轴向振动的线性叠加，并忽略引信对战斗部动力学模型的影响，则可用图4所示的多自由度弹簧- 质量- 阻尼系统[16]描述战斗部在侵彻过程中的运动特性。其中，战斗部刚体运动是基础激励，各阶振动属于基础激励引起的强迫振动。图4中，f(t)为靶体响应力；mB为战斗部的质量，xB0为战斗部头部的位移，根据刚体运动计算；cBi、kBi分别为战斗部第i(i=1，2，…，N，N为振动阶数)阶轴向振动引起的等效阻尼、等效刚度，xBi为仅考虑战斗部第i阶轴向振动时引信安装位置处的位移。

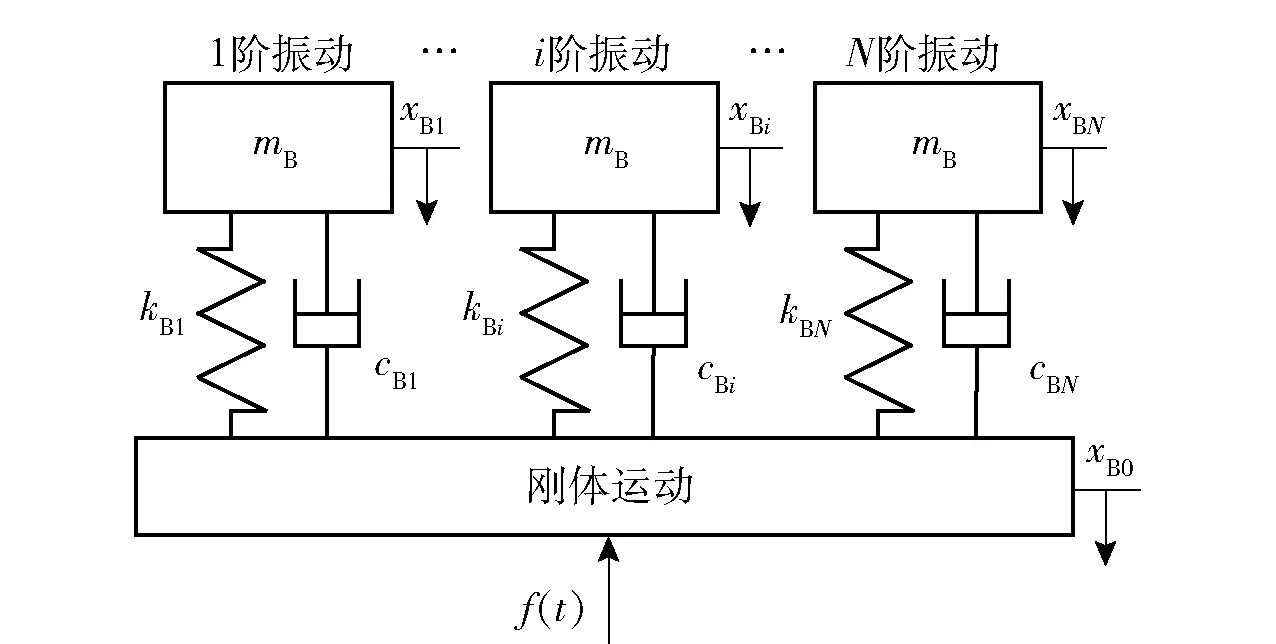
图4 侵彻战斗部动力学模型Fig.4 Dynamic model of penetration warhead

根据牛顿第二定律，可建立相应的动力学微分方程，即战斗部动力学模型如下：

(1)

等效刚度kBi、等效阻尼cBi与战斗部第i阶轴向振动固有频率fBi密切相关，如(2)式所示，各阶轴向振动固有频率可通过求解应力波波动方程得到[17]，如(3)式所示：

(2)

(3)

式中：ωBi为fBi对应的圆周固有频率；ξBi为无量纲阻尼比；L为战斗部长度；E0为战斗部壳体材料的杨氏模量；ρ为战斗部壳体材料的密度。

为了分析方便，记xBF、aBF分别为引信安装位置的总位移与总过载，如(4)式所示：

(4)

(4)式中总过载包含刚体过载与振动响应过载[18]两部分，刚体过载与靶体响应力一致，振动响应过载由轴向振动产生。

2.2 引信防护系统动力学模型

为了达到衰减高频应力波的目的，选用的缓冲材料波阻抗很低，杨氏模量仅为几十或几百兆帕，远远低于金属材料的上百吉帕。因此，战斗部轴向振动会引起引信内部电路模块的强迫振动，可等效为一个双自由度弹簧- 质量- 阻尼系统[16](见图5)。其中，与战斗部近似固连的引信机械壳体充当基座的角色，电路模块属于被防护对象，可等效为质量块，缓冲材料的弹性变形可衰减高频应力波，等效为具有阻尼特性的线性弹簧。图5中，mF为引信电路模块的质量，cF、kF分别为引信防护系统的等效阻尼、等效刚度，xF为引信电路模块相对于初始位置的位移。

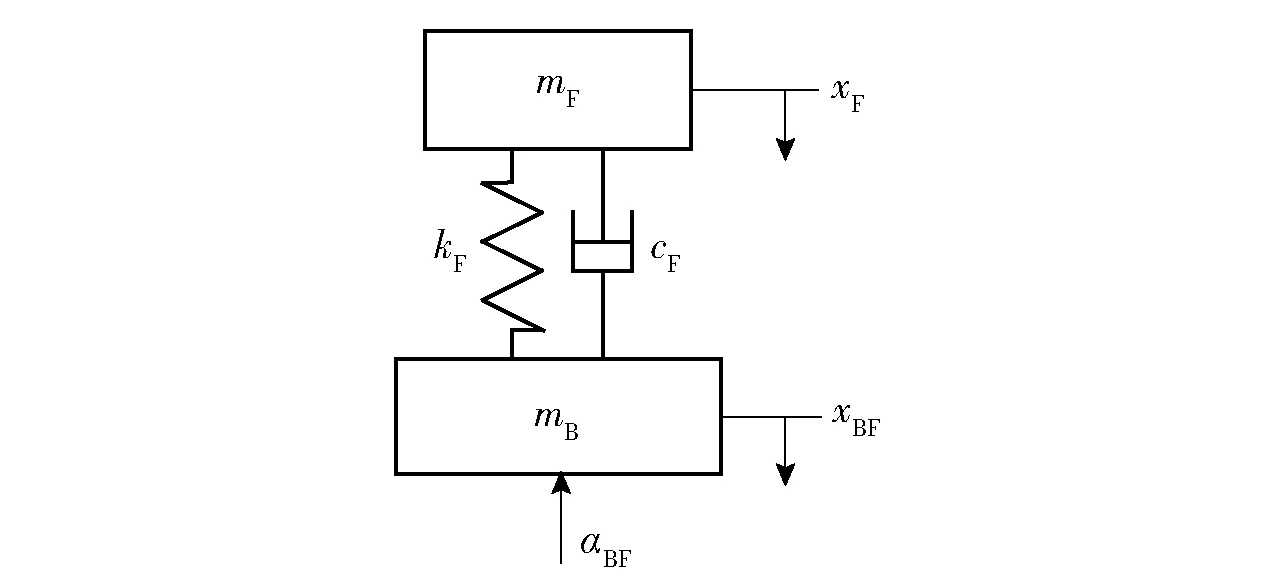
图5 引信防护系统动力学模型Fig.5 Dynamic model of fuze protection system

对系统进行受力分析可知，引信电路模块仅受缓冲材料弹性变形引起的弹簧力与阻尼力，引信机械壳体除受缓冲材料弹性变形引起的弹簧力与阻尼力外，还受战斗部的加载力。根据牛顿第二定律，可得双自由度系统的动力学微分方程，如(5)式所示：

(5)

式中：等效刚度kF、等效阻尼cF与引信防护系统密切相关，

(6)

ωFn为引信防护系统固有频率，ξF为引信防护系统无量纲阻尼比，可根据谐响应分析得出。

由于侵彻战斗部质量远大于引信电路模块质量，即mB≫mF，可忽略电路模块受力对侵彻战斗部的影响，此时(5)式可简化为(7)式，即引信防护系统动力学模型：

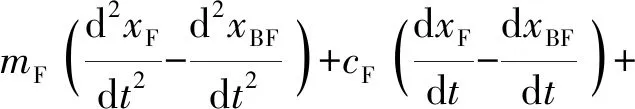
(7)

(1)式、(7)式所示的动力学微分方程相叠加，便可得到侵彻战斗部- 引信系统动力学模型。由于忽略了引信电路模块受力对侵彻战斗部的影响，两个动力学微分方程是解耦的，战斗部响应特性是引信防护系统动力学模型的输入，并直接影响引信响应特性。

3 谐响应分析

为了分析战斗部、引信在侵彻过程中的响应特性，需要已知固有频率与阻尼比等动力学参数。为此，以155 mm火炮平台发射的侵彻战斗部- 引信系统为研究对象，利用有限元分析软件Ansys进行谐响应分析[19]。

3.1 侵彻战斗部谐响应分析

建立的侵彻战斗部有限元模型(见图6)包括战斗部壳体、模拟主装药、引信，在头部施加载荷。战斗部直径0.15 m，弹长0.89 m，弹头系数3.1，弹质量约90 kg. 详细的材料参数如表1所示。

图6 战斗部有限元模型Fig.6 Finite element model of warhead

表1 用于战斗部仿真的材料参数
Tab.1 Material parameters for warhead simulation

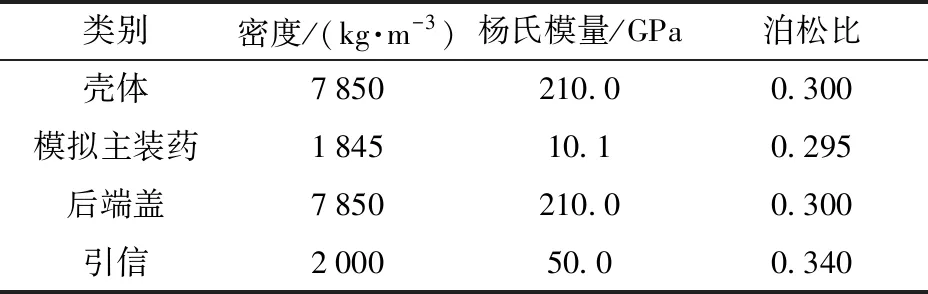
类别密度/(kg·m-3)杨氏模量/GPa泊松比壳体7850210.00.300模拟主装药184510.10.295后端盖7850210.00.300引信200050.00.340

仿真完成后，提取引信安装位置处的过载变化曲线，放大倍数(振动响应过载稳态峰值与刚体过载稳态峰值的比值)如图7所示。

图7 战斗部谐响应分析结果Fig.7 Analyzed result of harmonic response of warhead

根据图7可辨识出侵彻战斗部轴向振动的固有频率与阻尼比。由于高频加载比较复杂，本文取前3阶轴向振动进行研究，固有频率分别为2 730 Hz、5 650 Hz、8 100 Hz，与(3)式的前3阶固有频率计算结果基本一致，误差在10%以内；对应的无量纲阻尼比约为0.021、0.047、0.148. 将上述参数代入(1)式，便可得到侵彻战斗部的动力学模型。

3.2 引信防护系统谐响应分析

建立的引信防护系统有限元模型如图8所示，包括机械壳体、缓冲材料、电路模块，并在模型底面施加载荷，详细的材料参数如表2所示。

图8 引信有限元模型Fig.8 Finite element model of fuze

表2 用于引信仿真的材料参数
Tab.2 Material parameters for fuze simulation

类别密度/(kg·m-3)杨氏模量/GPa泊松比引信壳体45002100.34缓冲材料15500.030.43电路模块13001100.34

仿真完成后，提取引信电路模块稳态峰值过载随频率的变化曲线，如图9所示。根据图9可辨识出引信防护系统固有频率约为4 200 Hz，无量纲阻尼比约为0.061，将参数代入(7)式，便可得到引信防护系统的动力学模型。

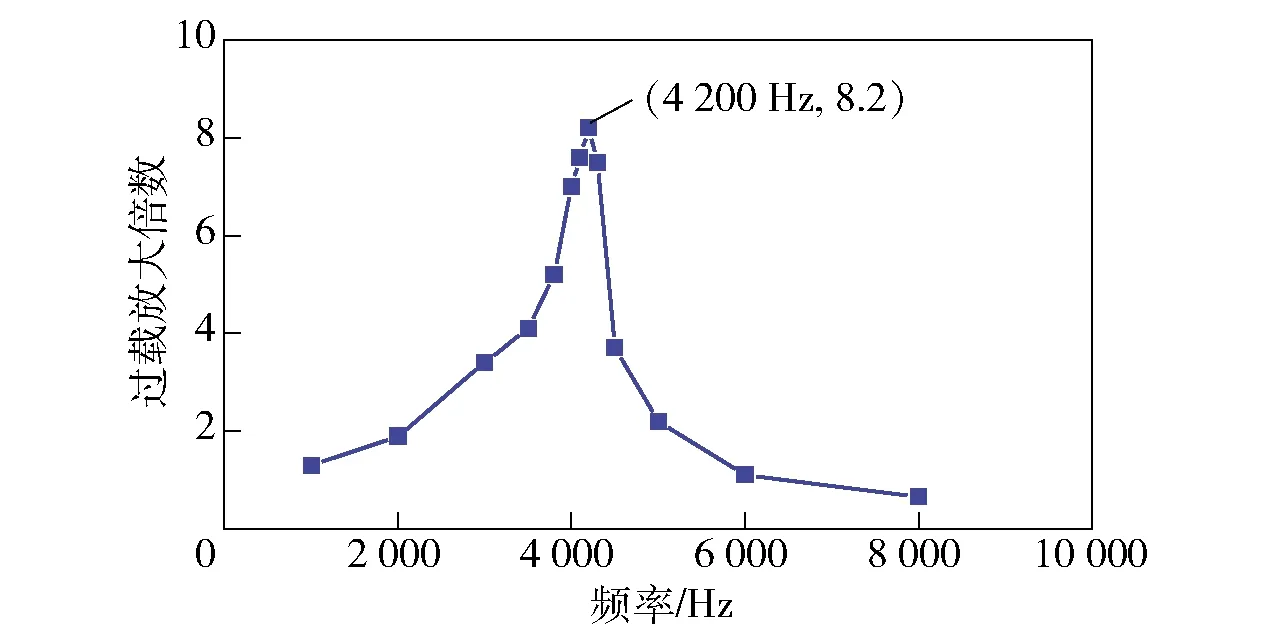
图9 引信谐响应分析结果Fig.9 Analyzed result of harmonic response of fuze

4 数值仿真计算

当靶体响应力与动力学模型参数已知后，便可采用数值积分的方法求解模型对应的动力学微分方程，并定量分析不同参数变化对引信响应特性的影响，进而指导引信优化设计。

计算时，选用4阶龙格- 库塔法求解，并通过C语言编程实现，详细的计算流程如图10所示。

图10 程序流程图Fig.10 Flow chart of program

以图6所示侵彻战斗部侵彻3.5 m厚C40强度靶和5层建筑楼板为典型工况进行数值仿真计算。计算时，分别用梯形窗信号、多个半正弦信号模拟战斗部侵彻强度靶、多层靶的靶体响应力(用战斗部刚体过载等效)，如图11所示，频谱分析结果显示两种输入信号的频率成分不同。侵彻强度靶时，属于单次加载，载荷持续时间比较长，主要是低频成分，能量集中频段在98 Hz附近；侵彻多层靶时，属于周期加载，每层的载荷持续时间比较短，没有明显的能量集中频段，但含有大量的高频成分，基频为250 Hz，与两层靶之间的飞行时间基本吻合。

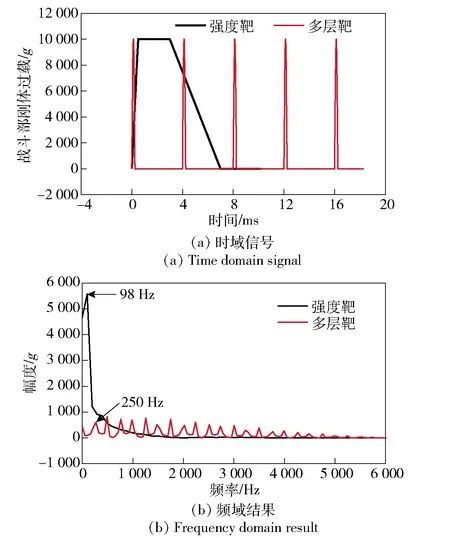
图11 靶体响应力Fig.11 Target response force

4.1 侵彻战斗部响应特性

战斗部振动响应过载变化曲线如图12所示。由图12可以看出，侵彻瞬间，引信安装位置表现出明显的前冲现象，即初始时刻的过载方向与输入信号相反。在同等输入峰值条件下，侵彻多层靶时的振动响应过载明显比强度靶振荡剧烈，前者峰值约是后者的几倍，甚至存在数量级的差异，该现象是由战斗部的幅频响应特性决定的。

对战斗部振动响应过载信号进行频谱分析，结果如图13所示。由图13可以看出：侵彻强度靶时，战斗部振动响应过载信号能量集中于2 748 Hz附近；侵彻多层靶时，战斗部振动响应过载信号能量集中于2 733 Hz附近，与战斗部1阶轴向振动固有频率(谐响应分析结果约2 730 Hz)基本一致，误差非常小。

图13 战斗部振动响应过载频谱分析结果Fig.13 Frequency spectrum of warhead vibration overload signal

对(1)式进行拉普拉斯变换，可得到以战斗部刚体过载为输入、以战斗部振动响应过载为输出的传递函数[20]，记为GR2V，

(8)

如果取N=3，传递函数对应的幅频响应特性如图14所示，与图7所示的战斗部谐响应分析结果保持一致，表明本文建立的侵彻战斗部动力学模型是准确的。

图14 战斗部幅频响应特性Fig.14 Amplitude-frequency response characteristics of warhead

由图14可以看出：当战斗部作为一个自动控制系统响应靶体响应力时，振动响应过载信号的能量主要集中于1阶轴向振动固有频率附近；当靶体响应力中的高频成分与战斗部某阶轴向振动固有频率相近时，战斗部会发生明显的谐振现象，导致振动响应过载大幅增加；侵彻多层靶时，靶体响应力含有大量的高频成分，使得战斗部振动响应过载值很大，是侵彻强度靶的14倍，与图12结果一致。

战斗部总过载变化曲线如图15所示。由图15可以看出：与输入信号相比，战斗部总过载发生了明显变化，已由单方向的变化规律演化为周期振荡变化，特别是侵彻多层靶时；靶标不同时，引信安装位置的载荷特性也有明显区别；侵彻强度靶时引信主要承受压缩载荷，侵彻多层靶时引信既承受压缩载荷也承受拉伸载荷，两种载荷的幅值相当。

图15 战斗部总过载变化曲线Fig.15 Total overload curve of warhead

对战斗部总过载信号进行频谱分析，结果如图16所示。由图16可见：侵彻强度靶时，战斗部总过载信号能量集中频段与靶体响应力基本一致，且在战斗部1阶轴向振动固有频率附近存在又一能量集中频段，但幅值已经大幅降低；侵彻多层靶时，由于战斗部的剧烈振动，战斗部总过载信号能量集中频段与靶体响应力差别较大，主要集中于战斗部1阶轴向振动固有频率附近，表明侵彻不同靶标时，战斗部具有明显不同的响应特性。

图16 战斗部总过载频谱分析结果Fig.16 Frequency spectrum of warhead total overload signal

4.2 引信响应特性

引信电路模块的过载变化曲线如图17所示。由图17可见，与图15所示的战斗部过载相比，引信内部电路的过载峰值更高，表明该仿真条件下引信防护系统会进一步放大冲击载荷，该现象是由防护系统的幅频响应特性决定的。

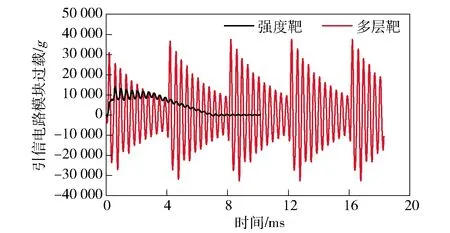
图17 引信电路模块过载变化曲线Fig.17 Overload curve of circuit module in fuze

对(7)式进行拉普拉斯变换，可得到以战斗部过载为输入、以引信电路模块过载为输出的传递函数，记为GB2F，

(9)

对应的幅频响应特性如图18所示，与图9所示的引信谐响应分析结果保持一致，表明本文建立的引信防护系统动力学模型是准确的。

图18 引信防护系统的幅频响应特性Fig.18 Amplitude-frequency response characteristics of protection system for fuze

对于本文仿真条件，战斗部1阶轴向振动固有频率小于引信防护系统的固有频率，对应幅频响应的放大区，此时引信过载会比战斗部过载值大，与图17所示的结果一致。

对引信电路模块的过载信号进行频谱分析，结果如图19所示。由图19可以看出，信号的能量集中频段与战斗部总过载一致，而在引信防护系统固有频率附近并没有明显的能量集中频段，表明战斗部轴向振动特性是影响引信电路模块过载的首要因素。

图19 电路模块过载信号的频谱Fig.19 Frequency spectrum of circuit module overload signal

综合上述谐响应分析与数值仿真计算结果，可得到如下结论：

1)以机械振动理论为基础的侵彻战斗部- 引信系统动力学模型建模方法是合理的，并得到了谐响应分析结果的验证，为快速预测战斗部、引信在侵彻过程中的响应特性开辟了一种新的思路；

2)考虑轴向振动后，战斗部响应特性与靶体响应力有很大区别，表现出明显的振动放大特性与周期振荡特性，特别是侵彻多层靶时，为合理设计产品的抗高过载考核试验提供了理论依据；

3)战斗部轴向振动是影响引信电路模块过载的首要因素，特别是1阶轴向振动固有频率，在引信抗高过载设计时要予以密切关注。

5 火炮试验验证

为了进一步验证模型的有效性，开展155 mm火炮试验，靶标与试验弹分别如图20和图21所示。其中，试验弹内部安装有引信，可记录侵彻过程中的过载信号。

图20 靶标布置Fig.20 Schematic diagram of target

图21 试验战斗部Fig.21 Schematic diagram of warhead

引信内部实测过载信号如图22所示。由图22可以看出，实测过载信号与以空腔膨胀理论、微分面元法为基础的经验公式解有较大区别，变化规律已由单一方向的作用力演化为正负交替的周期振荡作用力，每层靶的过载峰值也变大，体现出了侵彻战斗部- 引信系统的振动放大效应。

图22 实测过载信号Fig.22 Measured overload signal

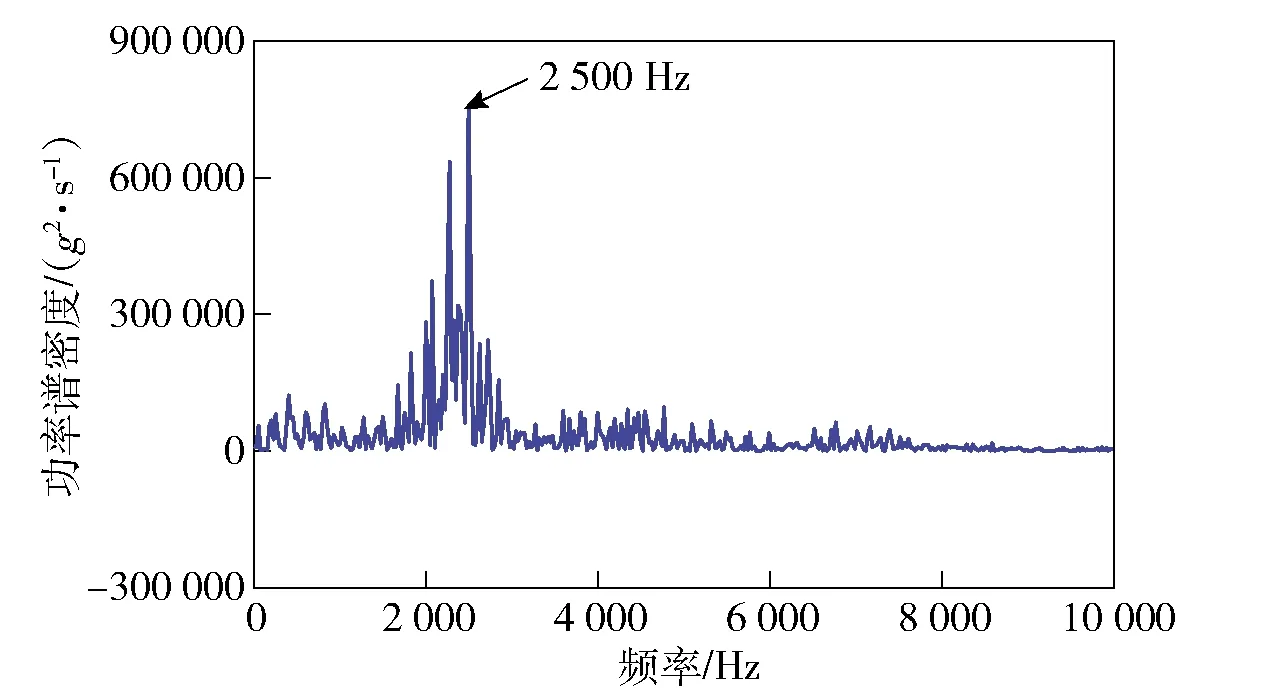
图23 实测数据的频谱Fig.23 Frequency spectrum of measured data

对应的频谱分析结果如图23所示。由图23可以看出，实测过载信号含有明显的高频成分，且信号的能量主要集中于2 500 Hz左右的频段，与试验弹的1阶轴向振动频率(谐响应分析结果约2 730 Hz)基本吻合，且未在引信防护系统固有频率(谐响应分析结果约4 200 Hz)附近表现出明显的峰值点，验证了战斗部1阶轴向振动是影响引信响应特性的首要因素。

6 结论

本文借助机械振动理论中的多自由度弹簧- 质量- 阻尼系统，建立了一种简化的侵彻战斗部- 引信系统动力学模型，通过谐响应分析确定了动力学模型参数，并采用数值积分的方法对侵彻强度靶与多层靶两种典型工况进行了动力学仿真计算，获得了战斗部响应特性、引信电路模块的响应特性。得出以下主要结论：

1)机械振动理论为基础的侵彻战斗部- 引信系统动力学模型能准确、快速地预测战斗部、引信在侵彻过程中的响应特性。

2)考虑轴向振动后，侵彻战斗部表现出明显的振动放大特性与周期振荡特性，而且是影响引信响应特性的首要因素，与传统的经验公式解有很大差异，可为引信等弹载产品的抗高过载优化设计提供依据。