小学“折纸+数学”教学的现状及对策

徐益钟

摘  要：在小学数学课堂中，小学“折纸+数学”教学的现状主要有四种情况：撒了谷子拾稻草——不分主次;放落斧头观景色——只看不做;浓烟浓雾里赏花——模糊不清;撤了火的钢精锅——很快变凉。针对这四种情况，文章提出了四种相应的措施：对着靶拉弓射箭——有的放矢;三国演义的许褚——赤膊上阵;十字街头贴告示——路人皆知;提着马灯下矿井——步步深入。

关键词：“折纸+数学”;现状;对策

小学数学教材中安排了四十几次的折纸活动，或启迪思维，或渗透思想，或探究新知，或巩固新知……符合小学生活泼好动与形象思维的天性。学生在不同折纸活动中经历动手操作、探究交流，培养学生获取知识的能力、分析和解决问题的能力，发展空间观念。笔者所任教的是一所集镇学校，调研了本校及本镇的一些学校后发现，由于折纸内容不进行笔试，所以导致有的教师无视这部分内容。其中主要存在四种现象，下面针对这几种现象谈一谈对策。

现状扫描一：撒了谷子拾稻草——不分主次

例如：二年级下册第32页例4《解决问题》。

师：剪纸艺术是我国的瑰宝，这节课我们就来剪纸。

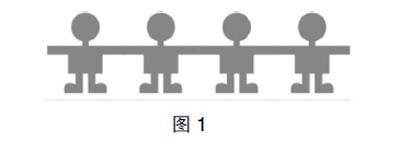
PPT出示例4题目：你能剪出像图1这样手拉手的4个小人吗？

师：谁来读一下题目？（生读）

师：你知道了什么？

生1：我知道了要剪4个手拉手的小人。

生2：4个小人大小要一样，还不能剪断。

师：一下子剪出4个小人有点难度，我们从剪1个小人开始，应该怎么剪呢？小组讨论一下。

生（讨论后汇报剪法）：先把长方形纸对折，在不是开口的这边画出半个小人，接着沿线剪开，最后展开就是1个小人。

师：小人为什么要画在不是开口的地方？

生：画在开口的地方就剪断了，小人就不能手拉手了。

学生动手尝试剪，教师展示作品。

师：1个小人你们会剪了，那2个小人又该怎么剪呢？小组讨论后交流。

生：剪2个小人要对折2次，在不是开口的这边画出半个小人，接着沿线剪开，最后展开就是2个小人。

学生剪后，教师把好的作品贴到黑板上，接着教学4个小人的剪法，方法同1个小人和2个小人。

师：不管剪1个、2个还是4个小人，我们都是怎么剪的？

生：先按小人个数进行对折，接着画出半个小人，最后沿线剪开后展开。

对策：对着靶拉弓射箭——有的放矢

上述案例中，教师对教材没有深入研究，也没有读懂文本背后的东西，只是对教材进行表面化的阅读，导致对重难点的把握发生了偏移，更不用说把握教材编排的精妙之处，创造性地使用教材了。这样的课堂就像撒了谷子拾稻草——不分主次，数学课成了手工美术课，为了折纸而折纸，没有抓住数学的本质东西，尽是一些花架子，教学活动无效，白白浪费了时间。此外，课堂教学内容单一，“折纸”有多少就教多少，不进行辐射性教学，没有拓展到剪8个小人、16个小人等。针对这种情况，我们不妨学一下渔人，把网鱼的大绳子提起来，网眼就一个个都张开了，鱼儿们就被网住了。道理是相通的，数学上我们也要抓住事物的关键，带动其他环节。学生的折纸只是一个载体，关键是教师没有引导学生利用作品展开数学思维。课一开始，教师可以先出示例4，请学生说一说“从图中，你获得了什么数学信息”。根据学生的回答，教师在黑板上板书例4的题目，再请学生说一说4个小人有什么特点，然后告诉学生剪4个小人有点麻烦，我们可以从剪1个小人开始。学生讨论好剪法后，动手操作，接着教师展示作品，然后提问学生：“为什么只画半个小人就可以剪一个完整的小人？利用了什么知识？折痕是什么？小人为什么画在不是开口的地方？”以同样的道理，教学剪2个小人和4个小人，最后汇报交流经验。在剪连续手拉手的小人的过程中，先剪1个小人，接着剪2个小人，再剪4个小人，这其实是数学上一种重要的数学思想——化繁为简。我们在剪的时候要注意什么？剪出的小人个数和对折的次数有什么联系？根据剪出的小人个数和对折次数的规律，你能推算剪出8个手拉手的小人需要对折多少次吗？对折6次，能剪出几个手拉手的小人？7次呢？这样的折纸活动，体现出浓浓的数学味。

现状扫描二：放落斧头观景色——只看不做

例如：三年级上册第80页例2《长方形和正方形的特征》。

教师先用PPT出示一些四边形（如图2），然后提问学生。

师：昨天我们认识了四边形，你还记得它们有什么特征吗？

生：有四条直的边，有四个角。

PPT隐去其他图形，只留下长方形和正方形。

师：你知道这两个图形分别叫什么名称吗？

生：左边的图形叫长方形，右边的图形叫正方形。

师：对，我们把这两个图形请到黑板上。（在黑板上贴上长方形和正方形）这节课我们就来认识长方形和正方形的特征。（板书课题）请同学们大胆猜测一下，长方形和正方形有什么特征呢？同学们可以从边和角的特征去猜一猜。

根据学生回答，教师有选择地板书：

长方形的对边相等。

长方形有四个直角。

正方形的四条边都相等。

正方形有四个直角。

师：同学们猜得对不对呢？我们需要进行验证。可以用折一折的方法验证长方形和正方形的特征。

然后，教师拿起一张长方形纸和一张正方形纸折给学生看。通过动手验证，教师肯定了学生们的猜测。

接着，教师用三角板的直角去验证四个角是否是直角。

……

对策：三国演义的许褚——赤膊上阵

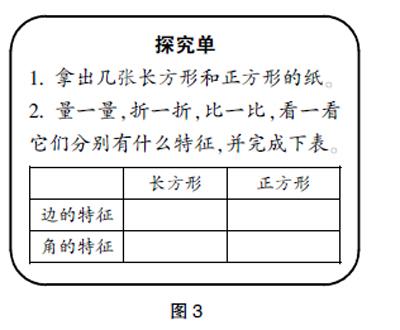
意大利教育家蒙特梭利曾经说过：“我看到了，我忘记了;我听到了，我记住了;我做了，我就理解了。”《数学课程标准》也指出：“动手实践、自主探索与合作交流是学生学习数学的重要方式。”上述案例中，探索长方形和正方形的特征时，教师成了主角，学生成了配角，只是听众，光看不做。教师虽然认识到动手操作的重要性，但却怕控制不住，让课堂上又乱又吵;同时也怕学生折一折太浪费时间，就干脆故步自封，没有让学生成为三国演义的许褚——赤膊上阵。对于这种情况，筆者认为上述案例可以这样设计：教师引入课题后，请学生拿出几张长方形和正方形的纸，然后量一量，折一折，比一比，看一看，最后说一说长方形和正方形有什么特征，填写探究单（如图3），并想一想两者有什么异同。学生动手操作完成后再来说一说自己的发现。这样设计能给学生充足的活动时间和空间，把知识点的教学融入学生的操作活动中，学生在“量一量，折一折，比一比，看一看”的活动中体验和学习数学，教学效果会更好，学生的收获也会更大。

现状扫描三：浓烟浓雾里赏花——模糊不清

例如：二年级下册第29页例1《认识轴对称图形》。

师（PPT出示树叶、蝴蝶、天安门）：你看到了什么？这些图形有什么共同的地方？

生：左右一样。

师：左右一样，我们可以说这些图形都是对称的。

师：生活中你还见过哪些对称现象？

生1：蜻蜓。

生2：飞机。

生3：窗花。

师：你能用一张长方形的纸，剪出一个对称的图形吗？

（学生动手剪，然后教师展示学生作品。）

小结：像这样剪出来的图形都是对称的，它们都是轴对称图形。（板书课题）那条折痕就叫作对称轴。

……

对策：十字街头贴告示——路人皆知

上述案例中，学生在剪轴对称图形时，由于教师没有介绍清楚剪纸的操作步骤，导致有的学生画出整个图形再去剪，结果画得不是很标准，以致剪出的图形不是轴对称图形;有的学生虽然对折了再剪，但却在开口的地方剪，以致剪出的图形断开了，不是完整的轴对称图形;有几个后进生无从下手，在那里乱剪一气。笔者认为，上述案例中的剪纸环节可以这样设计：教师可以先出示图示（如图4），问问学生图示是怎样剪的，根据学生的回答把简要的步骤写在黑板上（板书：①折;②画;③剪）;也可以事先请学习能力强的学生来剪，并把它拍成微视频，在学生剪纸之前播放给全班学生看，看完后提问：视频中的学生是怎么剪的？这样通过图示或视频的讲解，就像十字街头贴告示——路人皆知，促使学生对剪纸的整体步骤和重难点有所理解，使折法更容易被学生掌握。不论是优秀生还是后进生，通过提示都能很直观地了解剪法，效果很好。在这节数学课中，剪纸只是一个道具，它是为学生学习数学服务的，所以对折纸方法的探索并不是本节课的终极目标，只要学生清楚步骤，会操作就可以了。本节课折纸活动的目标是让学生认识轴对称图形的基本特征。

现状扫描四：撤了火的钢精锅——很快变凉

例如：二年级上册第40页例3《直角的认识》。

师（PPT出示国旗、凳子、双杆）：在这些图形中，你能找到直角吗？

学生上台找到直角后，PPT抽象出直角的图形（包括直角标志）。

师：生活中你还在哪里见过直角？

生1：桌面上的直角。

生2：数学书封面上有直角。

……

师：要判断一个角是不是直角，可以用三角尺上的直角比一比。

播放视频（判断直角的方法）。

师：你会折出一个直角吗？折不来的同学请看图示后再折。（PPT出示图示，如图5）

学生折后反馈。

师：你会用三角尺画一个直角吗？

……

对策：提着马灯下矿井——步步深入

上述案例像撤了火的钢精锅——很快变凉。在抽象出角的定义后，教材上安排了一个任务——请学生用没有棱角的纸折一个直角。当学生折出直角后，笔者认为教师不应就此打住，而应利用学生折出的几幅作品进行拓展，请学生说一說自己发现了什么。学生通过观察发现：所折的直角大小一样，角的大小与所折的边的长短无关。这时，教师追问学生：“怎样验证你刚才的发现？”学生利用重叠的方法进行验证。拓展中，教师向学生渗透比较角的大小的一种重要方法——重叠法。适当的教学拓展延伸，就像往平静的水面扔进了一颗石子，泛起阵阵涟漪。一方面，它使本堂课的知识点得到落实和升华;另一方面，它为学生的后续学习进行了铺垫。教学中，有许多数学教师非常重视课堂内容的拓展和延伸，让教学内容由易到难、由浅入深、由课内向课外相机渗透，既丰富了学习内容，又发展了学生的数学思维。我们可以从以下几个方面去深挖教材中的折纸内容，拓展学生的学习空间。

1. 巧用教材折纸例题，拓展学习空间。在教学中，教师要对例题进行深入研究，找出蕴含其中的数学思想方法，再引导学生进行探究，开拓新的思维空间。如：三年级下册第59页做一做：青青在一张长方形纸上剪下一个最大的正方形（如图6），剩下部分是什么图形？它的面积是多少平方厘米？学生完成此题后，进一步挖深：在长方形纸上剪下一个最大的正方形，怎样剪，正方形的面积才是最大的？

2. 深挖教材折纸习题，拓展学习空间。不管是哪种版本的教材，都不可能设计得天衣无缝，它或多或少会存在着“看不见”的空洞留白，我们教学时应把潜藏的探究内容挖掘出来，让学生洞察其中的奥秘，使教材在“无中生有”中变厚、增殖，拓展学生的学习空间。如：学习了人教版一年级下册《认识图形（二）》后，教材第7页第8题安排了折纸任务（如图7），学生完成此题后，进一步挖深：先观察一下“1”“6”的对面分别是几？再说说你发现了什么？由此发现规律：正方体表面展开后，相对面之间有一个面的间隔。

8. 折一折，用  做一个，“4”的对面是“（    ）”。

3. 精选辅助折纸材料，拓展学习空间。根据维果茨基的“最近发展区”理论，我们可以开发一些学生喜欢的、有趣的折纸内容，让学生通过对这些内容的学习，培养和发展思维能力，缩小现有发展水平与潜在发展水平之间的差异，以达到较高层次的智能发展水平。如：《折立方体》《在正方形中折最大的等边三角形》等。

总之，在课堂教学中运用好折纸教学，能让学生觉得学习数学是一件有意义、有挑战的事情，从而愿意亲近数学，钻研数学，引发数学思考，激发思维冲突，不断提升思维水平。