教学证据“块状印证”分析法例谈

方逸

摘  要：找准学生学习的起点，从学生的学情出发开展教学是保障教学顺利进行的前提。要想了解学情，可以多角度、全方位地收集素材，为教学提供证据。证据的多样性促使我们要对其加以分析。教学证据“块状印证”分析法可以做到去伪存真，使证据发挥最大作用并服务于教学，为教学判断与决策提供支持。

关键词：教学证据;分析;“块状印证”分析法

“学生目前的知识水平在哪个层次？以往学过的知识学生还记得多少？学生的认知能力处于哪个水平？学生调用知识的能力怎样？”等一系列问题的回答与解决都要立足于真实可靠的证据之上。只有如此才能叩响基于证据开展教学的大门。

证据一词从法律（听到它就让人联想到法律）角度和生活角度来讲，都是一个耳熟能详的词汇。证据是指能够证明某事物的真实性的有关事实或材料。从词汇的释义中可以分析出：（1）证据是事实或材料;（2）证据是真实的;（3）证据与要证明的事物具有相关性，而且这种相关性是必要且充分的。它们自身的真伪和之间的相互逻辑关系都需要分析与推理。作为指向、为教学服务的证据也具有相同性质与问题。对证据的判断与分析是利用证据开展教学前的首要与必备的工作。对证据进行甄别、判断与分析的方法有许多，“块状印证”分析法能有效剔除无用信息与证据，找出诸多现象背后的成因，为教学亮出有力证据。

一、“块状印证”分析法样式

确保收集证据的质量，需要运用多种方法收集多方面的信息，除了学生、教师主观方面的信息之外，还要包括数据等客观信息，因为教学中的许多问题不仅仅是教师与学生主观臆测就能反映出来的，还需要客观检测、评价。有些时候要运用两种甚至多种方式收集证据，如问卷调查、访谈、检测等，以弥补与佐证它们各自的缺陷，比如教师以往的经验、学生自我判断等主观性比较强，再比如试题检测中学生的思考过程难以呈现等。

收集整理信息时，要让信息成为教学判断、决策可以参考的证据，通常要经过一个甄别过滤的过程，在此过程中，需要运用“块状印证”分析（在研究某些人类行为的过程中，使用两种或两种以上的资料收集方法……是一种证明同时效度的有力方法），形成有效的证据块。只有当证据块内部证据之间能够相互印证，没有矛盾时，这样的证据才是高质量、高信度的证据，得出的结论才愈加接近客观事实。

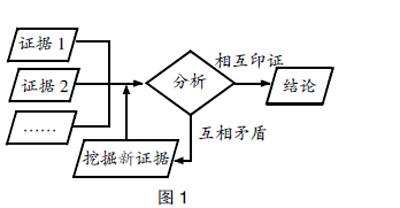
“块状印证”分析法样式（如图1）：

图1

首先通过多种途径与方法收集证据，组成证据块，将证据块中的证据进行对比分析，如果分析得出的结论是一致的，则说明各证据之间相互印证，得出的结论可信。如果分析得出的结论之间存在矛盾，那就需要收集、挖掘新的证据后再分析，剔除伪证据，直至证据块之间能相互印证。

二、“块状印证”分析法案例简述

主题：学生，你真的会了吗？

教学内容是苏教版四年级（下册）第96页《多边形的内角和》。

这是一节“综合与实践”领域内的教学内容，如果用重知识轻探究的教学方式来实施教学的话，学生能很快掌握学习内容。但是，《数学课程标准》（2011版）中明确指出：经历有目的、有设计、有步骤、有合作的实践活动;结合实际情境，体验发现和提出问题、分析和解决问题的过程……要想让学生经历实践活动的探究过程，首先要了解学生认知起点与认知能力。

1. 多途径收集证据

（1）证据1：教师以往的经验判断。这部分知识学生不会有意识地将前面学过的三角形内角和与多边形内角和相联系，推导过程中学生一般不会有意识地从一点有序分割多边形。

（2）证据2：问卷调查（如图2）。

《多边形的内角和》调查问卷

1. 你会计算一个多边形的内角和吗？

2. 你是怎样学会的？

A. 家长教的

B. 课外辅导班学的

C. 自己研究的

D. 上网或看书学的

如果上面选项没有，自己可以填写：

______________________________

图2

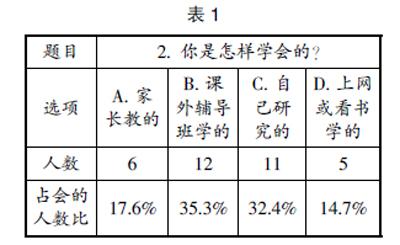
在全年级中随机抽选了50名学生参加问卷调查，第一题答对的学生有34名，占比68%。34名学生中第二题的回答数据统计情况见表1。

表1

（3）证据3：问题检测。对在问卷中回答“会”的34名学生进行试题检测（如图3）。

请你求出下面多边形的内角和，可以写一写、画一画表示出你的想法。

图3

检测试卷反馈的情况见表2。

2. “块状印证”分析

分析三种方式收集到的证据，并把分析的结论放在一起进行比较，相互印证（见表3）。

3. 挖掘新证据

为什么学生主观上认为自己会求一个多边形的内角和呢？要想解决这个问题，化解证据块之间的矛盾，就必须挖掘新的证据，将新的证据融入证据块中构成一个大的证据块，让其重构证据之间的联系。为此，教师找了几个自认为会的但是又不会解题的学生了解情况，访谈后得出这样的结论：学生认为求一个多边形的内角和就是将这个多边形每个内角的度数相加，但检测题中没有标出每个内角的度数，所以不会求（言下之意，是题目有问题）。

4. 再分析得出结论

证据块中加入新的证据后，前面分析产生的困惑豁然开朗。教师设计的问卷中“多边形的内角和计算方法”与学生心里理解的含义不同。学生直白、朴素的理解蕴含着一般化的求法，即所有（不仅仅是多边形的内角和）求和问题都要用加法计算解决。而教师指向的是边数相同的多边形虽然形状可能千变万化（每个内角度数不一樣），但是它的内角和始终不变（固定值），也就是多边形内角和只与多边形的边数有关，与它的形状无关。通过对证据之间相互印证分析得出的结论，从多个角度界定了学生的认知水平与能力，为教学提供了客观而充分的证据。