数学思想在初中数学教学中的渗透

王亚媛

[摘  要] 渗透数学思想对于提升初中生的数学核心素养具有重要的意义和作用. 在初中数学教学中，应关注学生在课堂上对数学思想的认识和应用，并引导学生将数学思想有效的应用在课堂中. 在初中数学课堂上，渗透类比思想，可培养数学推理能力;渗透数形结合思想，可提升问题解决能力;渗透化归思想，可培养数学解题能力.

[关键词] 初中数学;数学思想;渗透

众所周知，类比思想、数形结合思想、化归思想是常见的数学思想，合理运用这些思想往往会成为我们解决问题的关键. 初中学生普遍具有一定程度的数学基础，但仍未对数学学习形成系统的思维认知. 教师在教学中引入数学思想进行学习指导，能够有效引导学生透过现象看本质，并主动通过数学思想去解题，有利于培养其主动探索的学习习惯. 在初中数学课堂教学中，教师应关注学生对数学思想的认识和应用.

渗透类比思想，培养数学推理能力

类比思想在初中数学应用较多，是较为重要的数学思想，能够探索定理、概念、法则、公式等. 在初中数学教学中，恰当地应用新旧知识的类比，有利于理解、掌握新知识，还能让旧知识得到巩固，同时拓展学生的视野. 类比思想的引入一方面能够让学生快速理解数学知识的本质特点，提升学生的学习水平;另一方面能够培养学生开拓创造的意识和能力，从而进一步促使学生数学推理能力的提升.

1. 在概念教学中渗透类比思想

初中数学概念具有相似性高、难以区分的特点，因此教师在教学相似性高的数学概念时，可以充分利用类比思想，即从已经学习过、同时学生掌握较好的数学概念入手，在原有的知识上通过类比创设数学情境，引发学生关于新概念的好奇和思索，在学生发现不同和变化时，适时为新的概念进行定义. 这样能够很好地推动学生在两个概念中形成同一思维，进而使学生充分理解要学习的新概念.

例如在教学“分式”概念时，教师将小学的“分数”内容引入进来，与要学习的“分式”内容进行类比，寻找两者的相似与不同之处. 分式与学生小学已学的分数联系紧密，具体操作时教师通过引导学生回顾分数知识，以激活其原有的认知结构，为新知识的类比学习打下基础.

通过类比思想的教学手法，能够促使学生对比新旧两个概念之间的异同之处，也能够指引学生主动发现二者的联系，为新概念的教学提供有力的基础支持. 根据这一方法，学生能够更加清晰顺畅地认识、理解新概念. 同时需要教师注意的是，有时利用类比思想推断出的概念未必完全正确，教师在课堂上应注重论证学生得出的结论，避免其形成错误的概念认知.

2. 在定理、公式教学中渗透类比思想

类比思想的应用不仅体现在数学概念方面，还体现在数学定理与数学公式方面. 在数学定理与数学公式的推理过程中，类比思想被广泛应用，利用两个对象的类似性进行对比进而推导出结论，是较为常用的推导手法.

如通过三角形全等判定定理类比出三角形相似判定定理：全等三角形的判定定理有边角边公理、角边角公理、角角边定理、边边边定理、直角三角形中的斜边直角边公理，那么相似三角形的判定是否有类似的定理呢？又如通过线段垂直平分线的相关知识，类比出角平分线的相关性质和判定定理. 由此不难发现，这些定理之間都存在很多相似之处，很容易将两个判定定理联系起来，教师可以在学生原有的知识基础上，灵活运用类比的方法串联相关的知识，便于学生正确记忆定理，为学生日后在解题过程中运用定理打下坚实基础.

渗透数形结合思想，提升问题解决能力

由于初中学生受抽象能力不足所限，认为很多概念及定理都晦涩难懂，此时引入图形来教学能够很好地解决这一问题，使每一个概念和定义更加直观具体（符合学生的认知特点），便于学生领会. 因此，在教学晦涩难懂的数学概念或定理时，教师有必要引入数形结合思想，利用图形的直观性来理解抽象的数学概念，同时进一步将数学思想贯穿于学生的日常学习中，使学生养成利用数学思想解决问题的习惯.

如在教学等式两边加减同一个式子结果仍相等时，有些学生会认为这个过程比较抽象. 此时教师可以引入天平平衡的实例（利用PPT展示），引导学生把式子看成天平，很显然在天平两端加减相同质量的物体，天平两端依然保持平衡，让学生经历这一过程，从而帮助学生理解知识本质.

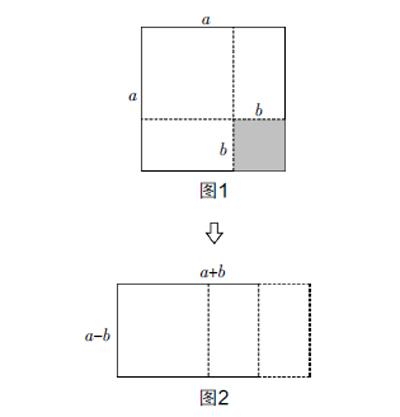
又如，为了让学生更直观地理解平方差公式，我们可引入数形结合思想.

我们知道平方差公式为：（a+b）（a-b）=a2-b2，可以将此公式与图形的面积结合起来. 如图1所示，我们作一个边长为a的大正方形，在其中作一个边长为b（b

渗透化归思想，培养数学解题

能力

相较于类比思想和数形结合思想，化归思想更为常见. 化归思想对于解决问题具有普遍的指导意义，它是最基本、最重要、应用最广泛的数学思想方法之一. 所谓化归思想是指将一种数学问题通过某种变换或手段转化为另一种数学问题，利用另一种数学问题形态来思考我们要解决的数学问题，一般是将陌生的、复杂的、抽象的问题转化为熟悉的、简单的、具体的问题，在这一大的概念背景下，类比思想和数形结合思想都可看作是化归思想的具体应用.

教师在教学过程中要积极培养学生的化归精神. 初中数学的所有内容几乎都存在着化归思想，不管是数学概念、定理，还是数学公式、性质，都有化归思想的影子. 教师在授课中，需要积极通过数学知识来培养学生的化归精神. 对于教师而言，化归思想的应用也有利于其顺利开展教学，进一步促进教学体系的完善，促使教师优化传统教学模式，使教师在知识系统的梳理过程中畅通无阻.

1. 化陌生为熟悉

学生往往对已经掌握的知识更加熟悉，应用过程游刃有余，在心理上也更加倾向于主动应用，但对于陌生的问题却不知从何下手. 此时，教师应引导学生开动思维，将不熟悉的问题转化为熟悉的问题进行解决，而不是在困境中一筹莫展，促使学生运用熟悉的方法解决问题.

例如，如图3，△ABC中，∠A=30°，∠B=45°，AC=2 ，求AB的长.

此问题用高中知识（正弦定理）很容易解决，但我们如何用初中知识解决这一问题呢？问题中涉及了两个特殊角：30°，45°，这两个角是我们所熟悉的，且常出现于直角三角形中. 问题要求的是边长，在直角三角形中，30°角、45°角与60°角所对的直角边与斜边或另一直角边有特殊关系，因此问题可转化为在直角三角形中利用特殊角所对边的特殊关系求边长，以此达到化陌生为熟悉的目的. 如图3，过点C作AB的垂线，交AB于点D，得到直角三角形ACD与直角三角形BCD. 由∠A=30°得出CD= AC= ，利用勾股定理得出AD;再由∠B=∠BCD=45°推出BD=CD，最后得出AB=AD+BD.

2. 化复杂为简单

化复杂为简单是化归思想在数学问题解决中最基本的转化过程. 我们在研究问题时可以发现，一个复杂的问题往往可以由若干个较为简单的問题组合而成. 这就给了我们转化问题的基础，利用知识之间的内在联系，将其转化成多个简单问题，逐一解决，各个击破，从而最终解决原有的复杂问题. 教师以这种方法引导学生对问题展开分析，能够降低对应问题的难度，同时让学生体验问题由繁到简的化归过程，帮助他们积累繁难问题的处理方法，提升解决问题的能力.

例如，有这样一题：设a是方程x2-3x+1=0的根，求 的值.

若由方程x2-3x+1=0得出a= ，再将其代入所求式子，过程显然过于复杂，那么有没有简单的解决问题的方法？“式子繁，先化简”是我们的基本认识，由a是方程x2-3x+1=0的根可得出a2-3a+1=0，同时我们还可得到两个变形式，a2-3a=-1，a2+1=3a，我们现在要思考的是通过这三个式子能否达到将原有式子降次的目的.

= =

= = = =

=a2-3a=-1.

综上所述，教师在初中教学中应用数学思想进行教学，能够简化教学过程. 教师应灵活运用数学思想，优化教学方式，将数学思想潜移默化地渗透进初中数学教学过程中.