基于ANSYS Workbench的锭子模态分析

吴云珍

(经纬智能纺织机械有限公司，山西 晋中 030601)

0 引言

在环锭细纱机的加捻与卷绕机构中，锭子是其重要的部件之一，它是用细长回转轴作为主体的结合件，主要用来把纤维捻成纱并把纱绕在筒管上成一定形状。锭子的结构主要是由铝套管锭杆结合件与锭盘组成，二者通过装配结合成回转体。正常工况下，锭子在额定工作转速下运行，若此工作转速的频率与锭子的固有频率接近时，锭子就会产生共振现象，同时也会出现很大的振幅，我们把此时的锭子转速称为锭子的临界转速。由于锭子特有的细长回转轴结构形式，使得锭子在工作中极易出现自由振动、强迫振动、自激振动等现象。若在纺纱过程中出现这些现象，就会降低纺纱质量，还会引发机件磨损、功率消耗和噪声污染等危害。因此，很有必要对锭子进行模态分析。李京等[1]利用ANSYS软件对锭子进行了模态仿真分析，采用的约束条件为锭尖固定约束和滚动轴承处的轴承约束。周国庆等[2]利用ANSYS软件对锭子组合系统进行模态仿真分析，将锭子轴承的支撑部分简化为沿轴的周向等效分布的4个弹簧，约束采用弹簧-阻尼单元连接。

本文首先通过计算得出纺锭轴承的弹性基础刚度值，再以细纱机锭子为研究对象，在Creo 4.0软件中建立三维模型，导入ANSYS Workbench软件中对锭子进行模态分析，得出锭子前6阶模态值，最后再对纺锭轴承的弹性支承刚度值进行参数化分析。

1 纺锭轴承弹性基础刚度计算

1.1 DZ系列纺锭轴承参数

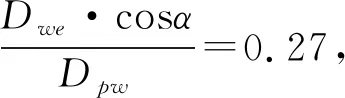
1.2 纺锭轴承的径向载荷计算

细纱机所配用的DZ系列纺锭轴承属于无内圈、单列向心短圆柱滚子轴承。向心滚子轴承的径向当量动载荷Pr(N)计算公式为[4]：

Pr=XFr+YFa.

(1)

其中：Fr为轴承的径向载荷，N；Fa为轴承的轴向载荷，N；X为径向负载系数；Y为轴向负载系数。

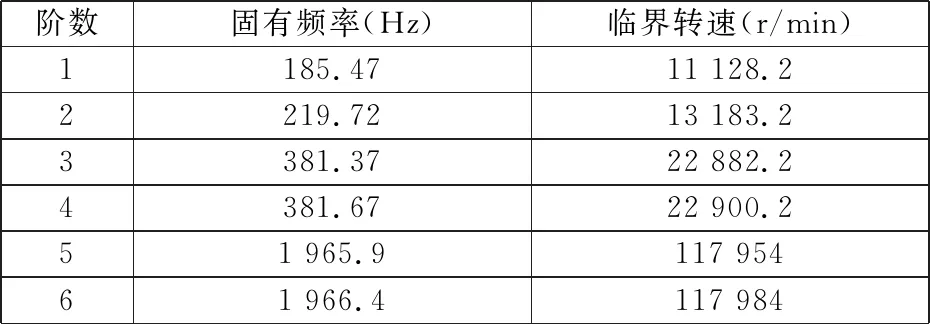
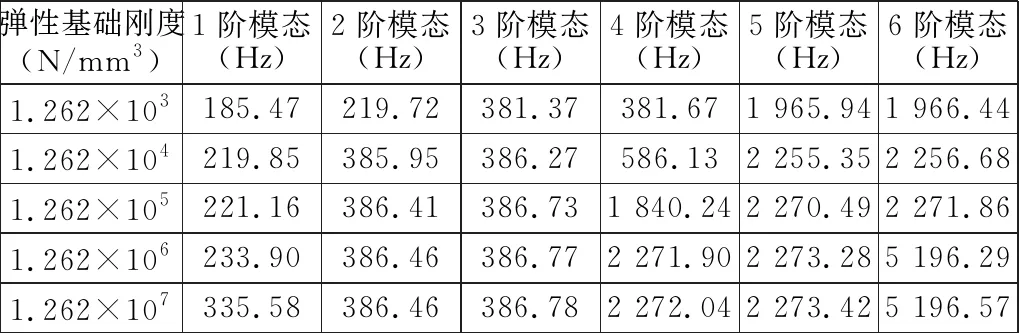
取滚子轴承的径向当量动载荷Pr=Cr=2 620 N，由于向心短圆柱滚子轴承主要承受径向载荷，因此选取轴承负载比Fa/Fr与分布参数e的关系为Fa/Fr

1.3 纺锭轴承的径向弹性位移计算

由于DZ系列纺锭轴承属于单列向心短圆柱滚子轴承，其径向弹性位移δ1(μm)计算公式为[5](游隙为零时)：

(2)

其中：La为滚动体有效长度，mm，La=L-2r，r为滚子倒圆角半径，r=0.2 mm。

将数值代入式(2)计算得：δ1=20.3 μm。

1.4 纺锭轴承的外圈与轴承座孔的接触变形计算

由于纺锭轴承的外圈与轴承座孔之间为过盈配合，因此在径向负荷的作用下，过盈配合表面会产生接触变形。接触变形产生的弹性位移δ2(μm)为：

(3)

其中：H为系数，取H=0.05。

将数值代入式(3)计算得：δ2=0.06 μm。

1.5 纺锭轴承内圈与锭杆轴径的接触变形计算

由于纺锭轴承内圈与锭杆轴径之间也存在过盈配合，同理，在径向负荷的作用下，过盈配合表面也会产生接触变形。接触变形产生的弹性位移δ3(μm)为：

(4)

将数值代入式(4)计算得：δ3≈0.14 μm。

1.6 纺锭轴承的弹性基础刚度计算

DZ纺锭滚动轴承的径向刚度计算公式为：

Kr=Fr/(δ1+δ2+δ3).

(5)

将数值代入式(5)计算得：Kr=1.24×105N/mm。

由于纺锭轴承与锭子的实际接触面积S=98.27 mm2，则纺锭轴承弹性基础刚度值为：

2 锭子模态分析

2.1 简化模型

锭子的主体结构是铝套管锭杆结合件与锭盘，而铝套管锭杆结合件又由铝套管和锭杆组成。在Creo 4.0软件中建立锭子的三维模型，再导入ANSYS Workbench软件的模态分析模块(Modal)中。简化后的锭子模型如图1所示。

1-铝套管；2-锭盘；3-锭杆

2.2 添加模型材料属性

锭子各零件所用材料及材料属性如表1所示。

表1 锭子各零件所用材料及材料属性

2.3 设定接触类型及划分网格

在模态分析模块的Modal-Mechanical界面中，为导入的三维模型自动检测接触面并生成接触对，各接触对的接触类型默认为绑定(Bonded)连接。模型均使用高阶的四面体网格(Tetrahedrons)生成四面体单元，设置网格尺寸为2 mm进行网格划分。检查网格单元质量(Element Quality)平均值为0.82，网格倾斜度(Skewness)平均值为0.26。根据网格划分倾斜度质量评估表[6]，可以判断出此网格单元质量较好。

2.4 边界约束条件

锭子在高速运转过程中，主要受到两个约束：锭尖处的约束和滚动轴承处的约束。仿真分析时将锭尖和滚动轴承处的约束均设置为弹性支承(Elastic Support)。因纺锭轴承与锭杆的实际接触长度为滚动体的有效长度，即La=4.6 mm，所以在锭杆上设置与轴承连接处的曲面长度为4.6 mm。根据已经计算出的纺锭轴承的弹性基础刚度值(Foundation Stiffness)，设置弹性支承(Elastic Support)值为1 262 N/mm3。锭子被施加弹性支承约束后如图2所示，其中，A为在滚动轴承处施加弹性支承约束，B为在锭尖处施加弹性支承约束。

图2 锭子弹性支承约束

2.5 模态分析结果

设置完成后进行模态分析，得到锭子前6阶固有频率和各阶临界转速，如表2所示。锭子的前6阶模态振型如图3所示。锭子的额定工作转速为15 000 r/min～18 000 r/min，所以不会发生共振现象。

表2 锭子前6阶固有频率及临界转速值

3 参数化分析

3.1 参数化模态分析

将纺锭轴承模态分析约束条件中的弹性基础刚度值(Foundation Stiffness)设为输入参数，模态分析结果中前6阶固有频率值设为输出参数。以1 262 N/mm3为参考刚度值，在参数设置(Parameter Set)中设置不同的输入参数值进行参数化分析，得到的结果如表3所示。

图3锭子的前6阶振型

3.2 分析结果讨论

若将锭尖和滚动轴承处的约束均设置为固定约束(Fixed)再进行模态分析，得到的前6阶固有频率如表4所示。由此可见，固定约束条件下锭子的固有频率值较高，而锭尖和滚动轴承处的约束均设置为弹性约束时，锭子的各阶固有频率值均降低很多，且设置为弹性约束更为接近实际情况。

从表3参数化分析结果可以看出，当纺锭轴承的弹性基础刚度值由1 262 N/mm3逐渐增大到1.262×107N/mm3时，锭子的各阶固有频率值呈增长趋势；当增大到1.262×106N/mm3及以上时，锭子的各阶固有频率值增长趋于平缓，说明此时弹性约束趋向于固定约束，其模态值已偏离实际情况。

表3 参数化分析结果

表4 固定约束前6阶固有频率

4 结语

本文通过计算得出纺锭轴承的弹性基础刚度值，再以细纱机锭子为研究对象，对其进行模态分析，得到锭子的前6阶模态值。最后对纺锭轴承的弹性支承刚度值进行了参数化分析，验证了计算得出的刚度值的合理性。此方法为锭子结构优化设计及减振方法的研究提供了重要的理论参考依据，同时也为研究其他模态分析提供了一种方法。