基于最小二乘原理的圆拟合及误差评定算法研究*

黄力峰，汪 伟，吴南星

(景德镇陶瓷大学 机械电子工程学院，江西 景德镇 333403)

0 引言

在机械产品的生产加工中，往往会遇到对圆形零件特征参数的检测和圆度误差的评定，以提高零件加工和装配的精度。在圆的参数求解中需要通过采集圆周上若干离散点的坐标，利用不同的方法求解出拟合圆的圆心坐标和半径，其方法有近似算法、非线性最小二乘法、最小区域法优化评定等[1]，其中最小二乘法分别由高斯和勒让德独立提出，是最早采用的拟合圆及圆度误差评定的方法，因其评定模型简单、易被工程人员掌握等优点而得到较为广泛的应用[2]。

在求解最小二乘圆的数学模型时，因其无法精确求解，需要对非线性方程组进行数值计算，国内外学者对最小二乘方法的适应性和精度提高等方面进行了研究。Kasa[3]提出了基于最小二乘原理拟合圆的方法，并研究了采集点沿圆周分布的情况对圆心和半径随机误差的影响。田社平等[4]给出了最小二乘通用算法，并与近似算法相比较，讨论两者的适用范围和计算精度。Chan Y T等[5]通过加权平均所有组合的计算中心作为求解方法，避免了最小二乘法中近似或优化带来的问题。王秀梅等[6]针对最小二乘方法求解提出了改进的混沌优化算法，并通过数据验证了算法的有效性。

在基于最小二乘法对圆参数求解时，有基于非线性最小二乘问题的最优化解法以及改变模型残差项的代数解法[7]两种方法。其中，最优化解法存在如何选择合理的初始值及迭代算法计算效率低等问题；而采用代数解法时，样本中噪声点即异常值的数量或采样集中等因素会导致拟合精度下降。本文研究了代数解法的推导过程和最优化解法中各类优化函数的最佳选择，以及噪声点数目及分布情况的不同等影响因素，利用MATLAB进行数据仿真计算，分析两种方法的拟合效果及计算精度，明确各方法的适用范围及优缺点，以实现最小二乘圆快速准确的求解。

1 最小二乘法模型的建立

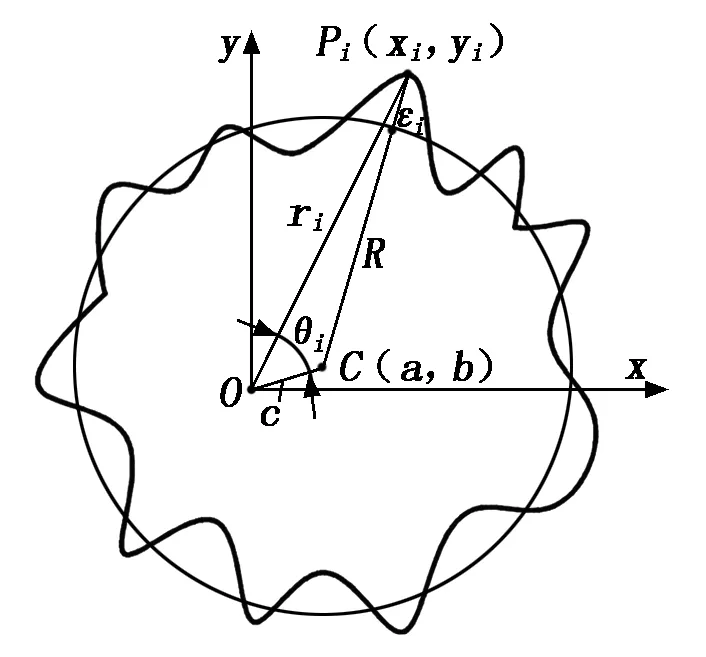
图1 最小二乘算法模型

使得各点到最小二乘圆上的距离的平方和最小，可得到模型一：

(1)

设最小二乘圆的方程式为：(xi-a)2+(yi-b)2=R2，可令残差项为：ei=(xi-a)2+(yi-b)2-R2，则模型二可表示为：

.

(2)

由于模型一存在非线性方程组求解困难等问题，只能采用近似或优化的方法求解[8]。针对模型二，式(2)中F的偏导数必须满足最小化的条件为：

令

D=n∑xiyi-∑xi∑yi.

(3)

(4)

(5)

(6)

(7)

联立式(3)～式(6)可解得模型二中A、B、C：

(8)

由式(8)可得到最小二乘意义下的拟合圆的圆心坐标(a,b)和半径R为：

(9)

2 优化算法的实现

MATLAB软件的优化工具箱(Optimization Toolbox)中含有一系列的优化算法函数，当使用最小二乘法对最小二乘圆参数求解时，可以利用求解多变量函数极小值问题的fmincon、fminsearch函数和非线性最小二乘问题的lsqnonlin函数进行优化求解[9]。而这些方法的收敛速度、求解效率和精度各不相同。引用文献[10]一组圆度测量数据，分别对三种函数进行测试，其计算结果如表1所示。

表1 各优化函数测试结果

此外，为测试三种优化函数对初始值的依赖程度，利用MATLAB中rand命令产生2 000组随机数作为初始值，三种函数达到全局最优的组数占比分别为17.7%、14.3%、44.55%，故模型一直接利用MATLAB中解决非线性最小二乘问题的lsqnonlin优化函数进行求解较好。该方法不涉及具体的算法，程序编制简单，求解精度较高，可通过如下设置求解：

[x，resnorm]=lsqnonlin(fun，x0，lb，ub，options).

其中，x为使用迭代法搜索的最优参数，为最小二乘圆的圆心坐标(a,b)和半径r；resnorm为各项误差，即目标函数的函数值；fun为目标函数；x0为变量的迭代初值；lb和ub为x值的上、下界，即x值的范围设定；options定为默认设置。

设i=1,2,…,n(n>3)为被测实际圆周上的测量采样点，最小二乘圆圆心坐标为(a，b)、半径为R，令目标函数为：

然后调用MATLAB优化函数lsqnonlin求得最小二乘圆的圆心坐标和半径。

3 数据仿真与分析

在仿真实验的设计中，已知样本(x1,y1),(x2,y2),…,(xn,yn),要求拟合出一个模型(函数)F，其预测值F(x)与样本实际值y的误差最小。考虑到样本数据并不是真实值本身，假设真实模型(函数)是f，则采样值y=f(x)+ε，其中ε代表噪声，所以拟合出函数后，可以采用偏差和均方误差函数来度量其拟合的好坏程度。故在圆心为a=0，b=0，半径R=10圆周上不同弧度范围内任意取n个样本点，分别加上一定比例均值为0、方差为σ2的高斯随机变量ε，σ∈[0,1]，从45°<θ<360°变化，n可取6、10、20、30，对每个不同的θ、n和σ值，生成数据以进行仿真实验，每组重复实验30次，以式(10)和式(11)计算每种方法的偏差B和均方误差M的值，其值的大小作为衡量优化方法和代数解法拟合圆效果的优劣评价指标。

(10)

(11)

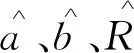
此外为验证各方法在计算圆度误差时的评定精度，从圆周上采集点均匀分布(12点)以及少量点集中分布(6点)两种情况，计算最小二乘圆的参数及圆度误差，并与文献[4]和文献[5]中的通用算法和质心法进行比较。实验数据分别为：

均匀采样12点：

x=[23.30，15.67，3.85，-9.02，-19.47，-24.70，-23.31，-15.68，-3.83，9.03，19.48，24.71]；

y=[9.05，19.47，24.70，23.31，15.68，3.83，-9.03，-19.46，-24.70，-23.30，-15.67，-3.81]。

离散采样6点：

x=[1.0，2.0，5.0，7.0，9.0，3.0]；

y=[7.0，6.0，8.0，7.0，5.0，7.0]。

仿真实验结果如表2所示，表2中，θ为所取数据的弧度范围。比较表2中两种方法计算所得的偏差值与均方误差值的大小(在零噪声条件下即理想模型的偏差和均方误差为0)可知：在小弧度范围内，随着噪声即σ的增大，两种方法的拟合精度和稳定变差，但优化算法优于代数解法，具有更好的拟合精度；随着弧度的增大至大部分圆周或整圆时，两种方法拟合圆精度大致相同且效果较好，能包容较大的噪声点，因此选择何种圆拟合法，视弧度、采集点数和噪声情况而定。

表3和表4分别为均匀采样12点和非均匀采样6点计算结果。表3结果表明：在采集点均匀分布情况下，各种算法圆度误差的评定精度相差不大。由表4可得出：对于采集点分布较集中的情况，代数解法计算圆度误差值较小，评定精度相对较高，但优化算法拟合效果比其余三种算法的效果要稍好，拟合效果如图2～图5所示。

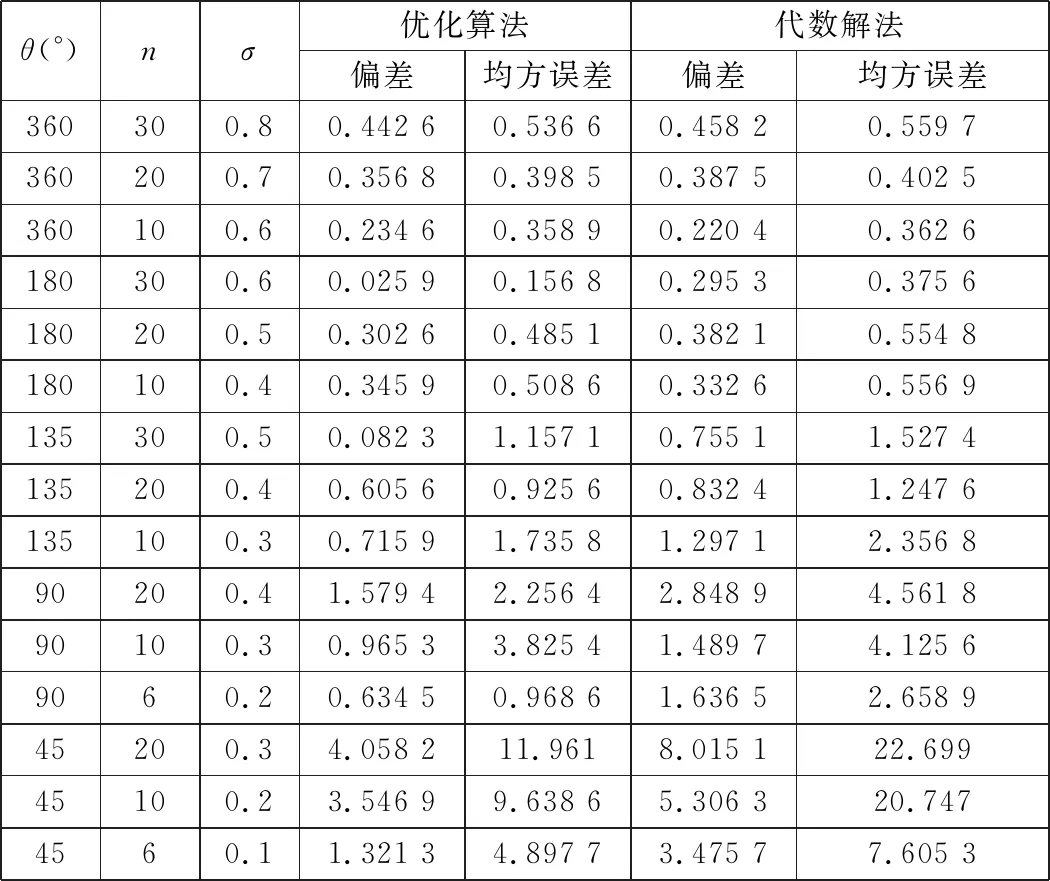
表2 两种方法计算结果

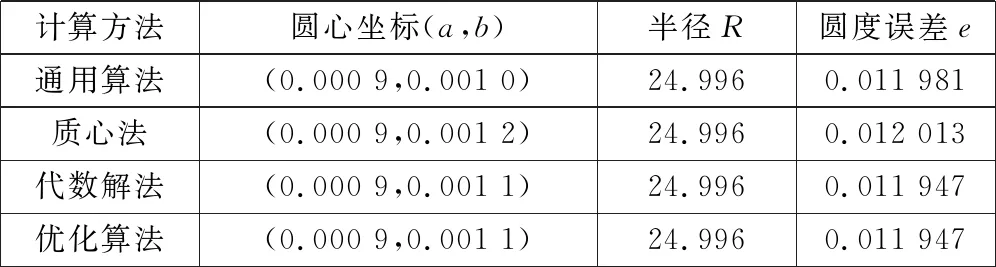
表3 均匀采样12点计算结果 mm

表4 非均匀采样6点计算结果 mm

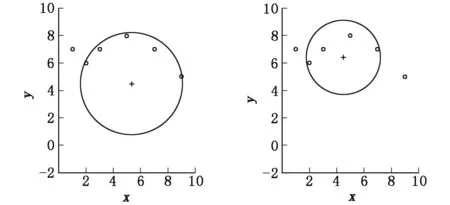
图2通用算法拟合效果图3质心法拟合效果

4 结论

研究了基于最小二乘法对圆拟合及误差的评定，对其中的优化算法和代数解法分别计算并进行比较分析。代数解法可直接求得准确的解析解，优化算法利用MATLAB优化工具箱选择了易达到全局最优解且计算效率较高的lsqnonlin函数进行优化求解。仿真实验结果表明：当采集点较多地分布在圆周时，优化算法和代数解法拟合圆的精度大致相同；当采集点较少且集中分布时，优化算法拟合精度更高，结果更加稳定；在采集点均匀分布在圆周上时，各方法计算圆度误差的结果基本相同；当较少的采集点非均匀分布时，代数解法计算的圆度误差值较小。本文提出的最小二乘算法能准确快速求解出圆的参数及圆度误差值，对实际中的测量应用具有指导意义。

图4代数解法拟合效果图5优化算法拟合效果