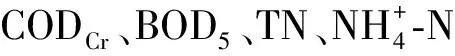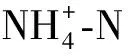瓦池污水处理厂进水水质特征及其对出水水质的影响分析

李嘉颖，姜应和，龚树毅，赵 俊

(1.武汉理工大学土木工程与建筑学院，湖北武汉 430070；2.公安县佳源水务有限公司，湖北荆州 434300；3.武汉理工大学供水与水污染控制研究中心，湖北武汉 430070)

拟定的污水处理厂设计进水水质是该厂污水处理工艺流程选择和污水处理单元设计参数确定的重要依据，污水处理厂实际进水水质与污水处理厂出水水质具有相关性，是污水处理厂运行调控的重要影响因素。因此，对污水处理厂进水水质特征及其对出水水质的相关性开展研究，对指导污水处理厂设计、运行和管理具有十分重要的意义[1-2]。

本文以公安县瓦池污水处理厂2017年全年实际进水水质资料为研究对象，分析各水质指标的变化规律；参照德国ATV-DVWK-A131E标准[3]确定污水处理厂的设计进水水质，与原先该厂的设计进水水质进行比较；根据污水处理厂进水和出水水质资料，分析各指标出水水质与进水水质的相关性。通过分析得到公安县瓦池污水处理厂的进水水质特征，为南方地区管网收集条件类似的污水处理厂设计和运行提供借鉴。

1 进水水质水量监测数据

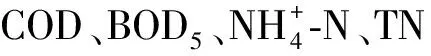
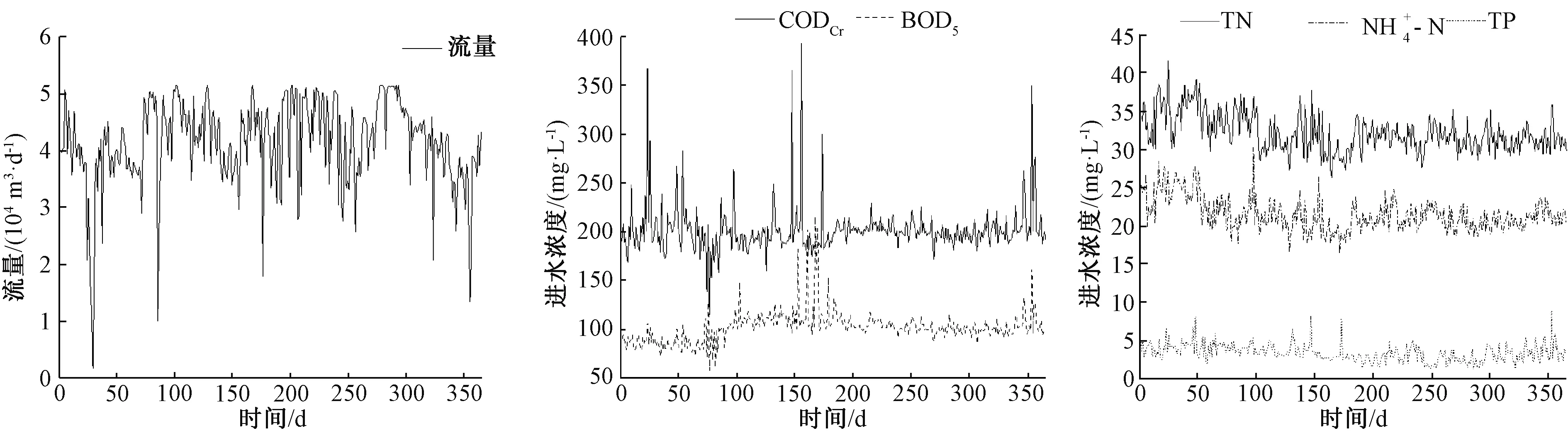
图1 进水水质水量监测数据Fig.1 Monitoring Data of Influent Quality and Quantity

2 各水质指标变化规律分析

以图1的进水水质实测结果为研究对象，分析各污染物指标年平均值、全年监测值变化特征、月平均值变化规律。统计分析运用EXCEL软件，作图软件运用SPSS 23.0和Origin 2016。

2.1 全年水质特征分析

以标准偏差、变异系数来判断数据的离散程度，以偏度和峰度来检验数据的正态性[4]。偏度大于零则表明某指标365个监测数据属于正偏态分布，小于零则属于负偏态分布，等于零则为正态分布。峰度是表征数据分布在平均值位置峰值高低的特征数，峰度大于零则峰部较尖，小于零则峰部更平缓，等于零则为正态分布。变异系数为标准偏差和平均值的比值，可比较不同数据组的离散程度大小。对图1中进水水质监测数据的分析结果如表1所示。

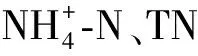
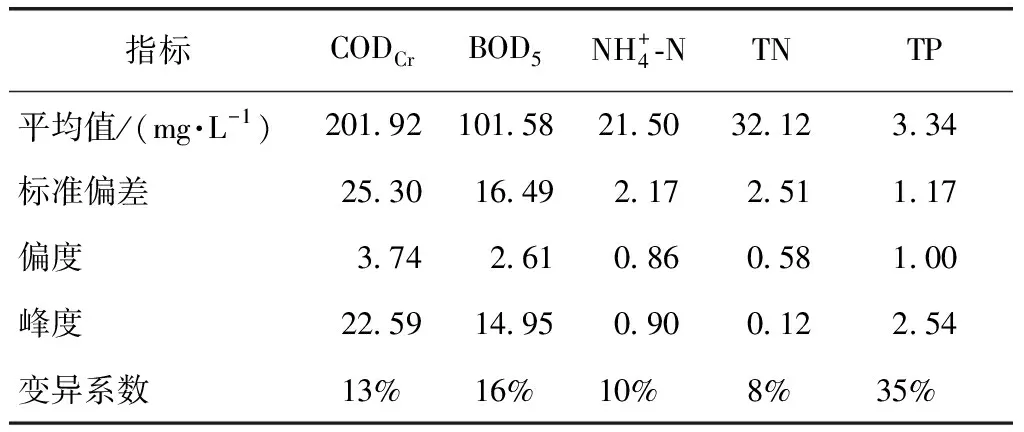
表1 各指标进水水质统计分析Tab.1 Statistical Analysis of Each Index of Influent Quality

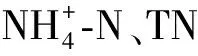
2.2 各月进水平均值变化规律分析

2017年各月处理水量及各指标进水浓度平均值如表2所示。

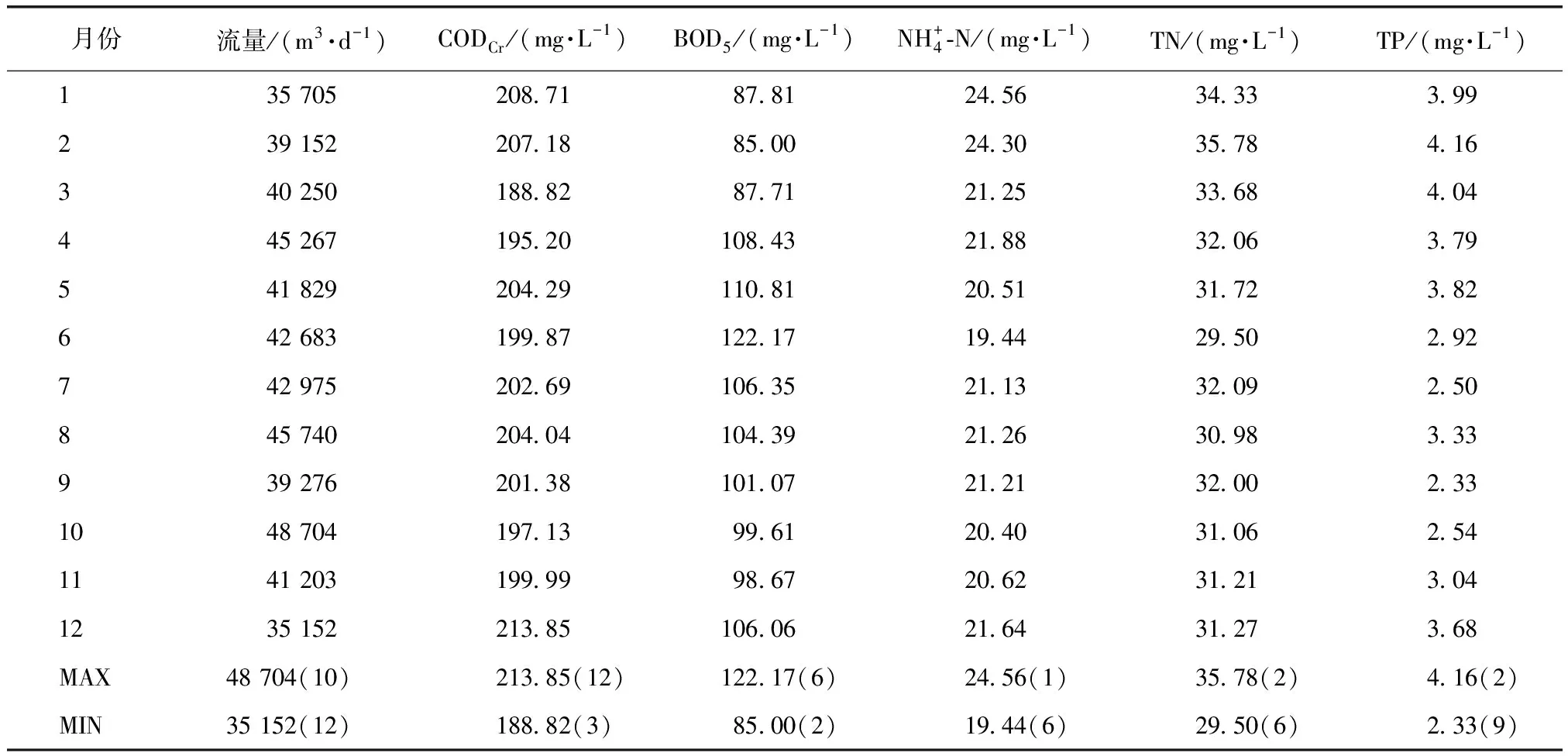
表2 各指标进水水质月均值Tab.2 Monthly Average Values of Each Index of Influent Quality

注：括号内为月份

3 设计进水水质可靠性分析

当有一定数量实测数据时，以一定保证率作为标准来确定设计进水水质较为科学合理[11]。德国ATV-DVWK-A131E标准[3]规定，当有40 d以上监测数据时，一般可采用85%保证率来确定设计进水水质。

首先将实测的水质数据进行汇总，然后从小到大进行排序，并利用式(1)计算小于等于某一浓度值的出现频率，即其相应浓度值的累积概率，计算结果如图2所示。

P=n/(N+1)

(1)

其中：P——某一浓度值的出现频率；

n——某一浓度值从小到大的序列号；

N——实测的水质数据的总数。

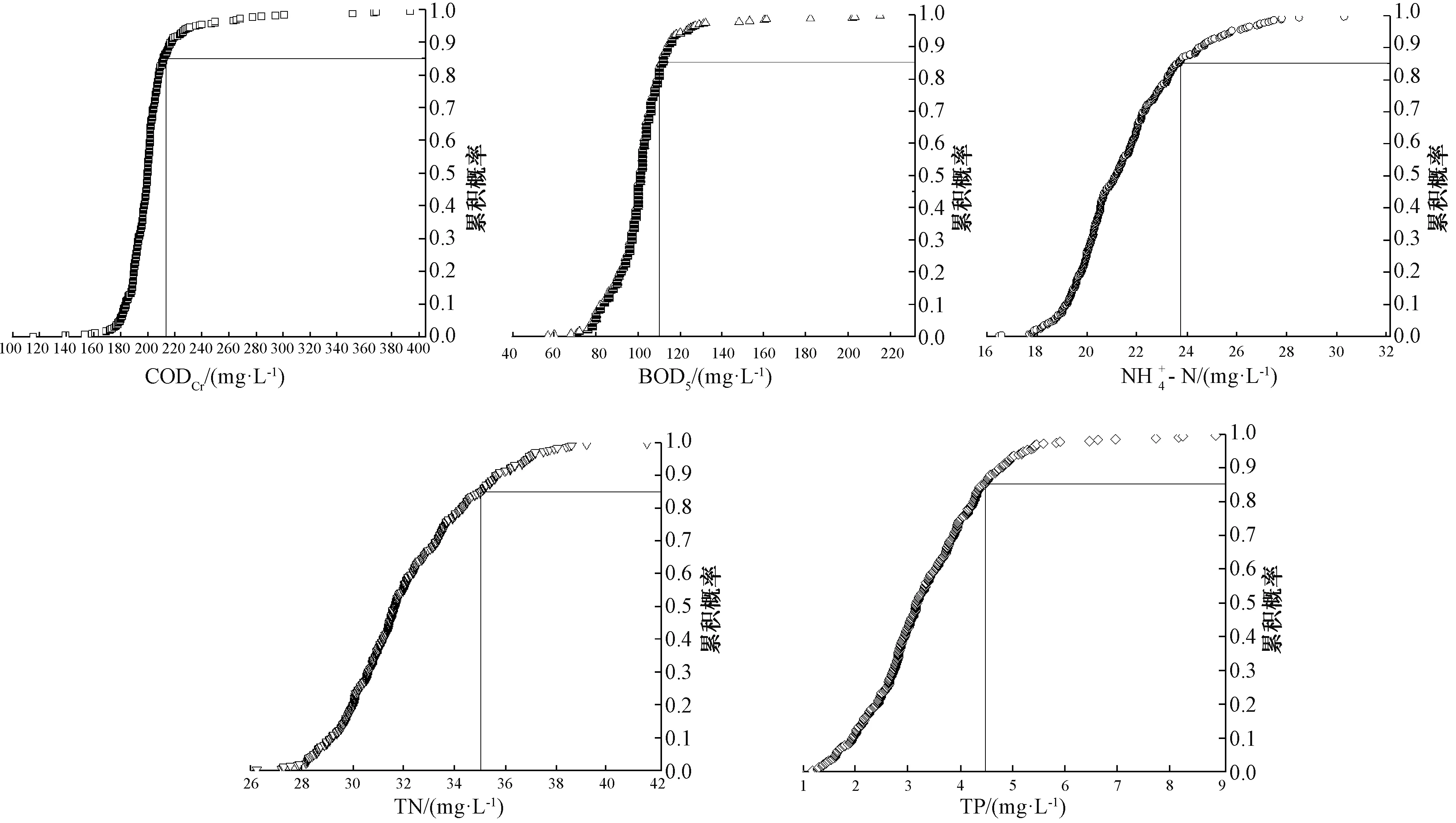
图2 各指标累积频率Fig.2 Cumulative Frequency of Each Index

该污水处理厂原先设计进水水质以及根据实际进水水质统计数据按ATV标准确定的设计进水水质如表3所示。

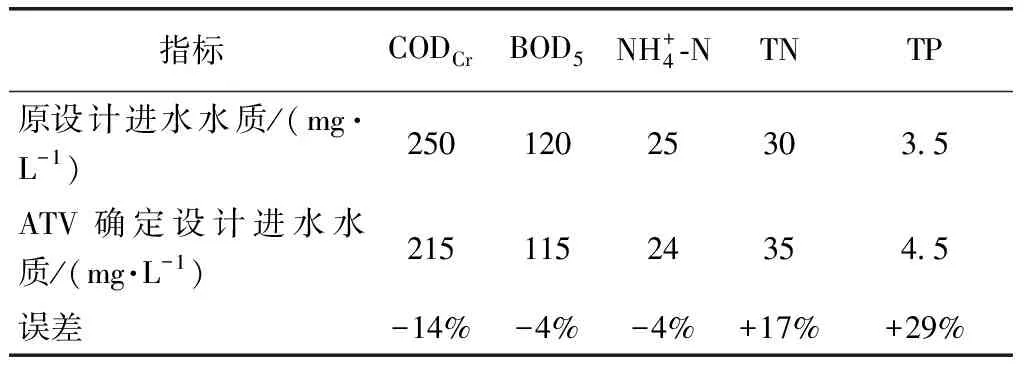
表3 设计进水水质对比Tab.3 Comparison of Designed Influent Quality Parameters

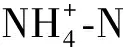
当进水BOD5为115 mg/L时，以BOD5=0.68 BODu[4]计，原水中总BOD即BODu，约为169 mg/L，即215 mg/L的CODCr中约有46 mg/L的CODCr是不可生物降解的，其中非溶解性不可生物降解的COD绝大部分被活性污泥吸附。BODu/TN=4.8，略大于4.0，基本满足生物脱氮要求；BODu/TP=37.1，远大于20，完全满足生物除磷要求。实际进水的TN和TP高于设计拟定值，且设计人员常采用COD作为可生化有机物量来分析生物除磷脱氮的碳氮比和碳磷比，导致设计时对生物除磷脱氮效果的预期往往较为乐观。该厂实际运行全年结果也表明，升级改造前该厂尾水出水TN达到《城镇污水厂污染物排放标准》(GB 18918—2002)一级A标准的概率约为90%，佐证了上述对脱氮碳源充足性的分析结果。

4 进水水质对出水水质的影响分析

4.1 污水处理厂出水水质监测数据

该污水处理厂2017年每日出水水质监测数据如图3所示。

对图3中出水水质监测数据进行统计分析，得到该污水处理厂出水达标情况如表4所示。

4.2 进水浓度对出水水质相关性分析

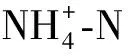
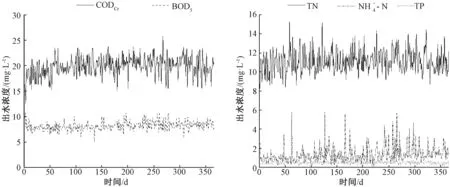
图3 出水水质监测数据Fig.3 Monitoring Data of Effluent Quality

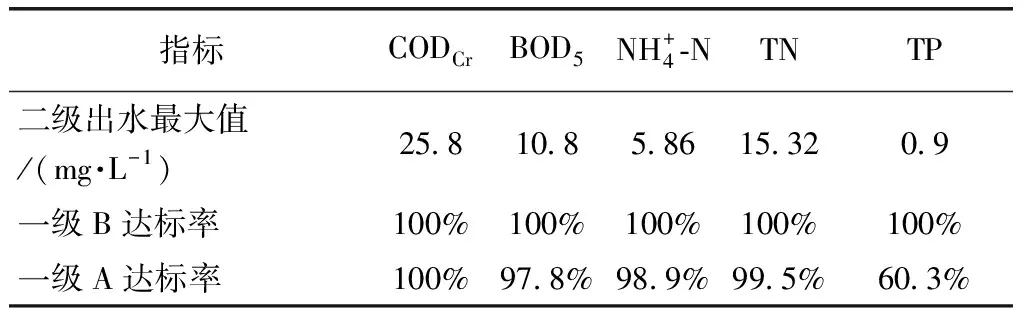
表4 出水水质达标率Tab.4 Qualification Rate of Effluent Quality

更符合正态分布，COD、BOD5和TP更符合正偏态分布。对皮尔逊系数法而言，其适用条件之一就是每个变量都应服从正态分布或接近正态分布；对斯皮尔曼系数法而言，其适用条件则更为宽泛，只要两个变量是连续的成对出现即可，但其统计效能相皮尔逊系数法略差一些。根据实际进水水质特点，选用斯皮尔曼系数法来判断进水水质对出水水质的影响。

根据图1和图3的进出水水质监测数据，利用SPSS 23.0计算各指标进水浓度对出水影响的相关系数，其结果如表5所示。

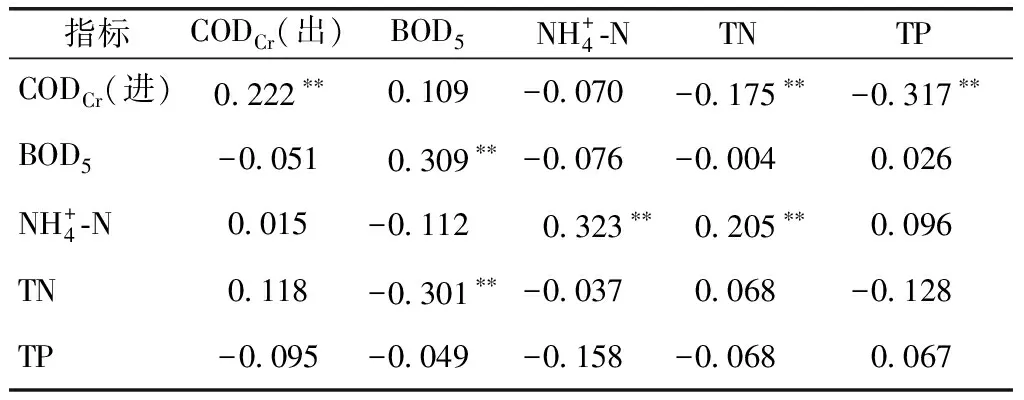
表5 进水水质对出水水质影响斯皮尔曼相关系数分析Tab.5 Spearman's Rank Correlation Coefficient of the Effect of Influent Quality on Effluent Quality

注：**表示在0.01置信区间内，相关性显著

5 结论

(2)除BOD5外，另外4个水质指标月均浓度最大值集中在气温低的春冬季；除COD、BOD5外，另外3个水质指标月均浓度最小值集中在气温较高的夏季。该厂进水水质随季节的变化规律与众多南方污水处理厂相似。