量子力学中的可能值与平均值

高峰，张登玉，彭琼

(衡阳师范学院 物理与电子工程学院，湖南 衡阳 421002)

到十九世纪末，关于机械运动、热现象、电磁现象及光的经典物理学已经建立了非常完善的理论体系，人们认为所有的物理规律都已经被发现，今后的工作只需要进行更精确地计算来完善物理学，并把这些规律运用到生产实践和生活中。但是，在十九世纪与二十世纪交替的年代里，人们发现问题很多：令人难以捉摸的热辐射现象，神奇的光电效应，不守规矩的低温下固体的比热等等，经典物理学都无能为力。庞大的经典物理学大厦开始出现了裂缝，特别是在解决黑体辐射问题中面临的紫外灾难及迈克尔逊—莫雷实验对以太的否定被号称为物理学晴朗的天空中存在的两朵乌云，使得当时几乎所有的物理学家都寝食难安。然而，正是这两朵令人不安的乌云却转化成了近代物理学诞生的彩霞，导致了量子力学和相对论物理的诞生，为尔后不断涌现的高科技、新学科、新技术的发展奠定了基础[1]。

量子力学是反映微观粒子(原子、电子、离子、原子核、基本粒子等)运动规律的科学。自从1900年12月17日德国物理学家普朗克(M.Plank)在柏林科学院物理学会的一次会议上，作关于尝试克服黑体辐射困难的报告中首次提出了能量子思想，至今已过去了近120年。如今，随着人们对自然现象研究的不断深入，完整的量子物理学理论已经在化学、生物学、材料学、宇宙学、信息科学等自然科学领域和许多近代技术中得等到了越来越广泛的应用[2-3]。

在经典力学中，任何物体的运动都可以被精确确定，描写物体运动学特性和动力学特性的物理量(如坐标、动量、角动量、能量等)在任何时刻都具有确定的数值。然而，在量子力学中，因为微观粒子具有波粒二象性，许多物理量就不能同时具有确定值，例如坐标和动量、时间和能量等，因此微观粒子没有确定的运动轨迹，描写它们运动学特性和动力学特性的物理量就具有了统计意义。尽管我们无法准确确定微观粒子在某一时刻的物理量数值，不过可以根据量子力学原理得到各个力学量可能的取值及其测得各可能值的概率，例如通过求解力学量算符的本征方程就可以求得该力学量的本征值，测量该力学量的可能值就是相应力学量算符的本征值。因此，研究力学量的可能值及其在任意态的平均值是量子力学中的重要内容[4]。本文主要介绍力学量可能值与平均值的基本知识及计算力学量可能值与平均值的基本方法，通过一些典型事例分析如何正确使用这些方法。

1 可能值与平均值

量子力学中的可能值是指某力学量可能取得的数值。前面已指出，由于微观粒子的波粒二象性，使得经典物理学中所定义的力学量在量子力学中有了新的意义，比如说，在某一时刻去测量粒子的坐标、动量、角动量、能量和时间等等，而试图指明它们各具多少数值，就毫无意义了。事实上，量子力学中的力学量必须用算符表示，力学量算符的本征方程及薛定谔(Erwin Schrödinger)方程告诉我们，所有力学量都具有一系列可能的取值。因此，求解力学量算符的本征方程就是获知力学量可能值的一种基本方法，下面证明测量某力学量的可能值就是该力学量算符的本征值。

根据量子力学的算符理论，任意态|ψ>可按一

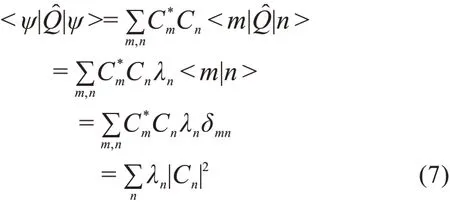
由(7)式可知，Q̂在|ψ>中 的Q值就独立地分属于 各分波了，其中λn为Q̂在|n>中的Q值，|Cn|2则为对应分波的强度，总的Q值就等于各分波之Q值之和。所以，将态按照Q̂的本征态实行谱的分解，可看作是对力学量Q进行的测量。假定入射粒子处于Q̂的本征态|1>，对应的本征值为λ1，按态的运动规律，它将到达接收器 ；如果处于Q̂的本征态|2>，对应本征值为λ2的粒子将到达接收器 ；等等。因此，接收器显示的每一结果将与Q̂的一个确定的本征态和本征值相对应，如图1所示。

图1 态的谱分解图

2 可能值和平均值的计算方法

在量子力学中，计算力学量的可能值和平均值是十分重要的内容。一般来说，计算力学量可能值有三种方法：(1)直接求解相应力学量算符的本征方程；(2)将给定的状态波函数按相应力学量算符的本征态展开，通过比较得出力学量的可能值；(3)利用算符的对易关系进行计算，例如通过引入上升算符和下降算符(Ĵ±=Ĵx±iĴy)可以求得任意角动量平方算符Ĵ2及其z分量算符Ĵz的本征值。在具体计算过程中，到底使用何种计算方法，要根据具体问题所给出的已知条件及计算要求而定。力学量平均值的计算通常有两种方法：状态平均法和概率平均法。状态平均法是计算平均值的一般方法，在已经给定状态函数的情况下，直接使用(9)式或(10)式进行计算。概率平均法是在已知或容易得到力学量各可能值及其取各可能值的概率的情况下，使用(7)式进行计算。但是概率平均法仅在力学量算符具有分离谱的情况下使用才是比较合适的，如果力学量算符具有连续谱时使用这种方法，计算仍然是不容易或不可能的。下面结合具体实例进一步说明在何种情况下使用哪种计算方法比较简单方便。

求粒子能?量的可能值及其相应的概率、能量的平均值。

解题分析：本题要求三个物理量，前面介绍了三种求力学量可能值的方法，求解相应力学量算符的本征方程是一般方法，相对说来这种方法比较复杂，后面两种方法只能在特殊情况下才能使用。考察一下本题给出的波函数，它是由三角函数表示的，而一维无限深势阱中的粒子的哈密顿算符(或能量算符)的本征函数也是三角函数，因此可以考虑将题目所给出的波函数按照一维无限深势阱中的粒子的哈密顿算符的本征函数展开。对于这类问题，特别要注意到利用三角函数的相关公式(如平方公式、倍角公式、积化和差及和差化积公式、等等)，而不需要按照使用(5)、(6)式的常规展开方法去展开。宽度为a的一维无限深势阱中粒子哈密顿算符的本征函数及本征值分别为

求动量的可能值及平均值。

解题分析：从本题已知的波函数来看，其形式是比较简单的，但若使用状态平均法来计算，则有该积分不收敛，所以不能使用状态平均法。现使用尤拉公式，有

在本实例中，因为粒子的定态波函数不是平方可积的，所以无法使用状态平均法计算粒子的动量平均值，但使用概率平均法却是有效的。

3 分析与讨论

量子力学是近代物理学的两大支柱之一，力学量算符理论是量子力学的核心内容[5]，本文主要讨论了量子力学中力学量的可能值和平均值的计算方法，由前面的分析可以得知计算力学量的可能值和平均值都有多种方法。在解决具体问题时到底使用何种方法，一定要根据具体情况灵活选择合适的方法。计算方法选择得适当，可以起到事半功倍的效果，否则，可能计算过程十分复杂，甚至无法得到所要的计算结果。特别是计算力学量的平均值时，状态平均法即(9)式或(10)式的使用是有条件的，条件就是状态函数必须是平方可积的，如实例三就不能用该方法计算。若要概率平均法和状态平均法都能够使用，通常情况下这要求(5)式中的级数|∑|m>Cm要一致收敛于|ψ>[6]，一致收敛的要求是比较高的，一般情况下，只要求平均收敛或者说均方收敛就可以了[7-8]。概率平均法的使用虽然没有条件限制，也只能在可以方便地求得力学量可能值及其相应的取值概率的情况下使用才是合适的。总之，在计算力学量可能值及平均值时，要具体情况具体分析，灵活选用适当的计算方法。