一道考研极限题的多种解法及可视化

王培颖，罗浩源，许清河，赵梓谷，谢绍龙，陈军羽

(广东技术师范大学 天河学院，广东 广州 510540)

随着每年考研人数的增多，考研的竞争力也越来越大。纵观考研数学，极限内容占有很大比重，下面以一个考研题说明极限的多种解题思路，并用数学软件验证了结果的正确性。

1 方法一：用四次洛必达法则

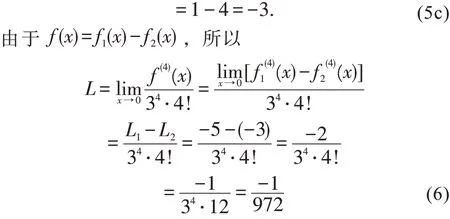
大部分同学会想到用洛必达法则，不过计算过程相当复杂，假如基本功不扎实，容易出错。

2 方法二：用四阶麦克劳林公式

结果完全相同。

3 方法三：用初等函数的四阶麦克劳林公式

由于

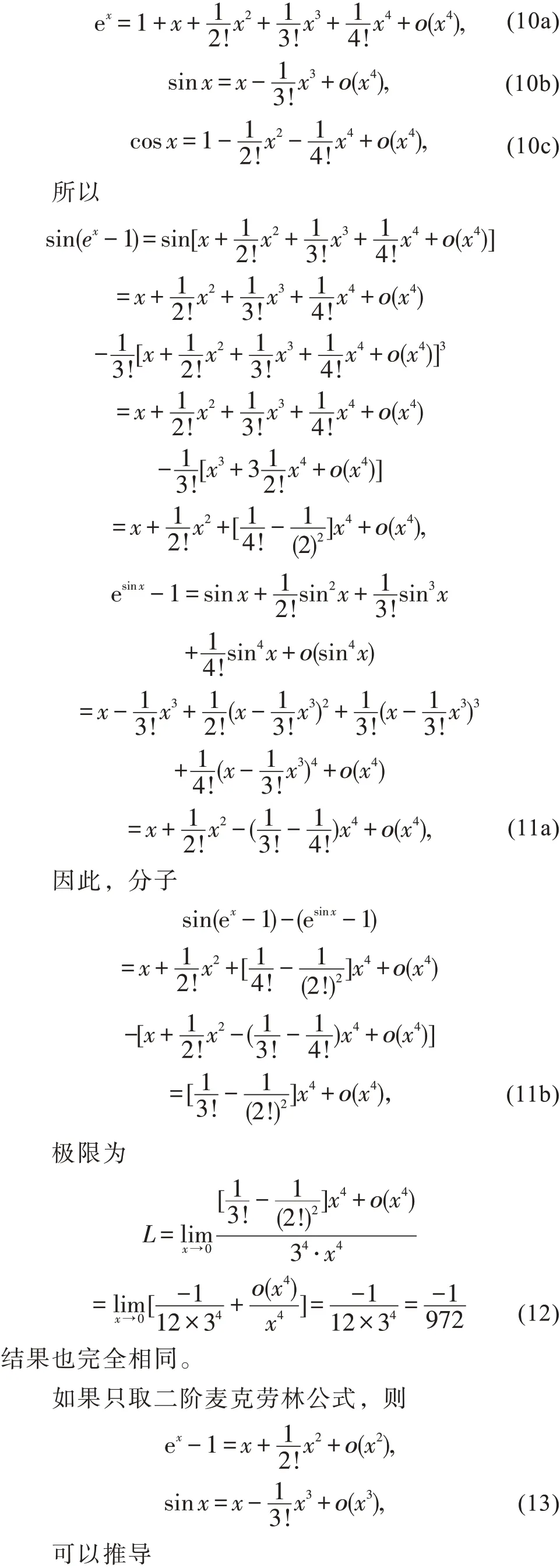
4 方法四：用一次洛必达法则和初等函数的三阶麦克劳林公式

结果仍然相同。

此题最容易出现的错误是将余弦函数单独取极限1，导致如下错误的解法：

5 方法五：用一次洛必达法则和拉格朗日中值公式

6 方法六：用一次洛必达法则和和差化积公式[2]

7 M ATLAB验证

在手工计算中很容易出现差错，设计几个小程序，用MATLAB的符号计算，很容易检验结果[3]。

M 1.m

%函数的极限(用洛必达中的各阶导数)

clear%清除变量

syms x%定义符号变量

f1=sin(exp(x)-1)%第1个符号函数

df1=diff(f1)%第1个符号函数的导数

d2f1=diff(f1,2)%2阶导数

d3f1=diff(f1,3)%3阶导数

d4f1=diff(f1,4)%4阶导数

L1=subs(d4f1,x,0)%4阶导数的值

f2=exp(sin(x))-1%第2个符号函数

df2=diff(f2)%第2个符号函数的导数

d2f2=diff(f2,2)%2阶导数

d3f2=diff(f2,3)%3阶导数

d4f2=diff(f2,4)%4阶导数

L2=subs(d4f2,x,0)%4阶导数的值

L=(L1-L2)/3^4/factorial(4)%极限

执行程序，可以检查公式(4a)~(4e)的正确性，再检查公式(5a)~(5e)的正确性，最后检查极限的正确性

图1

8 结论

采用多种方法求极限，是很好的思维训练，而用麦克劳林公式比较通用，学好麦克劳林公式可以更快速地求解极限问题。此题采用一次洛必达法则与和差化积公式最为简单，并且用MATLAB软件验证了结果的正确性。数学有一种“数形结合”学习方法，有些考研题目很难理解，MATLAB具有强大的绘图功能，可以将图形画出来，帮助学生理解，提高学习效率。