电磁式两自由度高效振动能量采集技术研究

王志华，吴丝竹，姚 涛，吕殿利，张惠娟

(1.河北工业大学 省部共建电工装备可靠性与智能化国家重点实验室，天津 300130；2.河北工业大学 河北省电磁场与电器可靠性重点实验室，天津 300130；3.河北工业大学 机械工程学院，天津 300130)

0 引言

随着不可再生能源的不断枯竭、环境污染程度不断恶化、化石能源消耗不断加大以及能源供应价格愈加紧张，风力发电、光伏发电、波浪发电等绿色发电技术得到快速发展[1]。与此同时，通信、物联网等技术快速发展，微电子系统(MEMS)系统、无线传感器和生物微纳机电器件等电子设备得到广泛应用[2]，这些电子设备的工作环境中存在比较丰富的振动能，这些振动能量收集起来可为通信模块、传感器等电子设备供电[3]。

电磁式振动能量采集技术的关键是设计高效的拾振机构。文献[4]研究了一种新型方形振子电磁低频振动能量收集装置，在2 m/s的振动速度下的感应电动势为4.8 V。文献[5]设计了一种四梁结构能量收集器，ncode_designlife软件的疲劳分析表明该结构能够经受3.092×1018次较高加速度冲击。郭庆等研究了一种新型回形弹簧能量采集装置，在振幅为500 μm的振动激励下，开路峰值电压可达1.82 V[6]。Podder P等人制作了非线性能量采集装置，具有在单独可调双稳态-二次、单稳态-四次和双稳态-四次电位中切换的能力[7]。上述文献主要研究了直线振动机构的能量采集技术，但是由于直线式振动存在动子行程短、频率低的固有缺陷，难以从根本上提高发电功率。美国的Harlem等设计了一种弹簧偏心转子的电磁能量收集装置，在±25°旋转振幅和1 Hz频率下能够产生最大61.3 μW的平均功率，但是由于采用了铁芯，电磁转矩较高，不适合车辆、波浪等位移振动输入的场合[8]。

振动能量采集装置的系统响应，主要基于振动模型等进行分析。基于三参数电磁能量采集模型，通过调整机械阻尼比和三参数系统刚度比增强了装置的能量转化效率[9]。李海涛等人分别采用龙格库塔和欧拉法分析了不同结构在确定性、随机性激励方式下的动力学行为，提高了系统的能量采集效果[10]。将电和热迭代模型与磁性傅里叶模型耦合成一个通用优化工具，可快速分析直驱非接触式圆筒状电磁式振动能量采集装置[11]。采用集总参数等效磁路模型优化后的磁路结构，可有效提高体积优值系数[12]。文献的分析结果表明，采用振动方程、磁场有限元分析和数值计算方法可以较好地分析振动能量采集过程。

负载也对振动能量采集装置有着明显影响。通过负载的调整，提高了能量采集的稳定性，并可检测出平均发电量[13]。非电阻元件的电负载对电磁振动能量采集装置有一定影响，调节电容器可以得到最佳负载电阻和最优的振动频率[14]。对于包含质量、弹性结构、电磁能量转换机构、电感、电阻和电容的振动能量采集装置，Cooley基于牛顿力学和基尔霍夫定律推导了电磁式振动能量采集装置的机电耦合模型，并根据该模型分析系统的动态特性[15]。

此外，压电陶瓷[16]、磁控形状记忆合金[17]等也可用于振动能量采集的研究，适合微瓦量级的供电场合。为了提高输出功率，将压电陶瓷与永磁体进行复合，可在一定程度上提高输出功率[18]。

增加振动系统的自由度可扩大能量采集器的采集区域[19]，提高拾振效率。本文提出一种新型两自由度电磁振动能量采集装置，将广泛存在的直线振动转换为动子的旋转运动。基于两自由度振动模型[20]和电磁感应定律，对该整套装置系统进行理论分析，磁场分布采用有限元法进行计算。最后，设计样机并将其固定到振动台进行测试和分析。该振动能量采集装置可使小车的水平振动位移比输入的位移激励放大了3倍，测试结果表明，在输入激励为斯柯达轿车的市区公路振动加速度谱下，测得的电动势平均有效值为8.47 V，其平均输出功率约为594 mW，可满足手机等电子设备的供电需求。

1 机电耦合特性分析

1.1 结构设计

直线式振动能量采集机构由于动子行程位移的限制，使得机电转换效率较低，并且动子与定子之间的相对运动频率难以得到有效提高。根据电磁感应发电原理，发电机的输出电压与动子的运动频率成正比。因此，提高振动能量采集装置的发电效率主要应从提高动子与定子相对运动频率和位移入手。这里提出一个两自由度高效振动能量采集机构，通过弹簧和摆杆，将较小的直线振动位移转换为较大的旋转位移，通过调整弹簧刚度、摆长等参数，提高振动频率。

所提出的振动能量采集装置结构如图1(a)所示。装置由外壳、弹簧、小车组成。顶部连接摆杆、动子，摆锤内部凹槽中放置4个永磁体，作为永磁发电的动子部分，小车前后壁上各装有均匀分布间隔一定弧度的线圈，每个线圈由若干匝铜线绕制，作为定子部分。双定子分布于转子两侧，利用小车结构巧妙组合在一起，保持动子与定子之间气隙距离在较小范围内，有效提高机械能到电能的转换效率。基于该结构制作了振动能量采集装置样机，其中永磁动子和感应线圈如图1(b)所示，拆掉一个侧板后的样机侧面视图1(c)，从图1(c)中可以清楚看到小车和拾振弹簧。

图1 振动能量采集装置结构图和实物照片
Fig.1 Structural drawings and photographs of vibrational energy acquisition devices

当振动激励作用到外壳上时，通过弹簧传动，带动小车左右晃动，同时小车内部的动子左右摆动，固定在小车上的感应线圈中的磁通开始发生变化，在电磁感应作用下线圈中产生一定的感应电动势，接上负载即可实现机械能到电能的转换。

振动能量采集装置的系统模型如图2所示。其中，X为装置左侧输入的位移振动激励，x为装置内部小车位移，θ为摆与竖直方向夹角，X、x和θ均为时间t的函数，l为摆的长度，h为摆顶端距离底部外壳长度，k1、k2分别为左右两侧弹簧的刚度，c1、c2分别为左右两侧的摩擦阻尼系数，摆上嵌入永磁体作为动子。此外，外壳、动子和小车的质量分别为M、m1和m2。

图2 振动能量采集装置的系统模型
Fig.2 System model of vibration energy harvester

1.2 动力学分析

对电磁式振动能量采集装置动态响应规律的分析需要掌握系统的阻尼、刚度特征，由于弹簧的质量和阻尼对系统影响较小，可忽略不计。下面对整个两自由度系统进行分析。

整个系统主要考虑水平方向振动激励对装置的影响，在弹簧的驱动下，小车内部的摆做单摆运动，位于摆两侧的定子线圈中产生感应电动势。因此，可采用等效的方法，对发电机装置进行两自由度分析。摆的坐标方程为

(1)

两端分别对θ求导，得到摆在水平、竖直方向上的速度分别为

(2)

当对外壳左侧施加激励时，系统的总动能T为

(3)

(4)

其中，Jc为摆的转动惯量。将式(2)和(4)代入式(3)中，整理系统总动能方程T为

(5)

由于弹簧的变形和重力势能，系统的总势能V为

m1g[yc-(h-l)],

(6)

将式(1)代入(6)，得到系统总势能：

(7)

由于系统作用有非保守力，可以计算与x和θ对应的广义力，可计算沿X方向的作用力F为

F(t)=k1[ls1-(x-X)]+k2[ls2-(X-x)]-

(8)

其中，ls1、ls2分别为弹簧起始长度。

利用拉格朗日方程建立系统的两自由度方程：

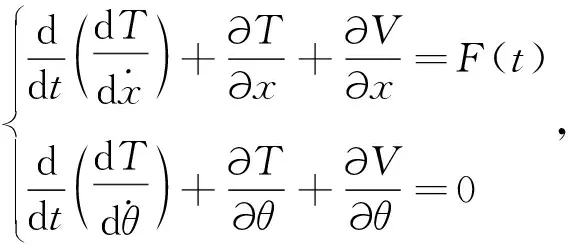
(9)

将式(5)、(7)代入式(9)中，推导出系统的运动微分方程为

(10)

将式(10)进行变形，得到小车位移x和摆的角度θ的二阶微分表达式分别为

{4l[m1lsinθ)θ2+(k1+k2+k1ls1-k2ls2)·

(11)

(12)

上述方程中，位移x和摆的角度θ之间存在耦合关系，在已知振动激励和系统模型的相关参数时，求解上述微分方程组的数值解即可求出小车位移x和摆的角度θ。

1.3 输出电动势分析

由于所设计的发电装置是在位移振动的激励下进行工作，动子上输入转矩小，因此，为了减少动子与定子之间的磁阻力，这里采用无铁芯式设计，这也导致磁场分布主要集中在永磁体周围，磁感应强度随距离的增加而衰减很快，为了提高线圈中的磁通值，应该让动子和定子线圈之间的气隙越小越好，这主要取决于加工和装配精度。

根据法拉第电磁感应定律，感应电动势与感应线圈中磁通的变化率成正比。而磁通的变化率与动子和定子的相对位移有关，动子和定子的相对位移与摆角θ(t)成正比，则线圈i的输出感应电动势Ui可表示为[15]

(13)

式中，i=1,2,…,9，ω为动子与定子的相对角速度，φi为线圈i的平均磁通。则N个线圈的总输出电动势为

(14)

由式(14)可以看出，提高振动能量采集装置的输出电动势，可通过下面两种方式入手：提高动子与定子的相对运动角速度，增加线圈中的磁通变化率。

2 仿真分析

基于前文的理论推导，对文中提出的振动能量采集装置进行仿真分析。非正弦的周期激励一般都可以分解为一系列正弦激励的叠加，这里对正弦振动激励下的响应进行分析。若给定外界输入振动位移激励为X(t)=20sin(20πt) mm。振动能量采集装置的相关参数为：两侧弹簧刚度均为2 N/mm，弹簧的初始长度ls1、ls2均为50 mm，阻尼忽略不计，摆长80 mm，动子由4个矩形钕铁硼永磁体和非导磁材料构成。

计算得到的小车水平位移和摆的角度分别如图3(a)和3(b)所示。从图3(a)可以看出，装置内小车运动水平位移x峰峰值约30 mm，比输入的位移激励大了约1.5倍，说明所设计的拾振机构可将振动位移放大，在双弹簧和摆的作用下，装置内部小车往复运动较为剧烈。图3(b)中摆杆的最大摆动角度可达约75°，较大摆动幅度和较快的运动频率有利于得较大的感应电动势输出。

图3 正弦振动位移激励下小车水平位移与摆的摆角的计算值
Fig.3 Calculated values of small cart displacement and swing angle under sinusoidal vibration displacement excitation

利用COMSOL有限元软件对振动能量采集装置的磁场分布进行分析。由于铝合金和铜的磁导率与空气基本一样，因此，外壳、摆杆、线圈对磁场分布的影响可以忽略，这里只展示永磁体和线圈中的磁场分布。其中，图4(a)为实体模型，图4(b)为永磁体上的磁场分布，图4(c)为线圈和永磁体磁场分布的侧视图。

从图4可以看出，磁场在离永磁体轴向约5.5 mm处，磁感应强度降到约0.2 T，边角部分的磁感应强度更低，因此感应线圈与气隙的总厚度不应超过5.5 mm，即：若气隙为1 mm，则感应线圈厚度不超过4.5 mm。

根据有限元软件计算得到的磁场分布计算结果，再结合动子和定子的位移方程和电磁感应定律，可计算得到能量采集装置的输出电动势U(图5所示)，其中9个感应线圈进行串联连接。

图5中，线圈输出电动势的峰峰值和有效值分别是15.96 V和7.31 V，平均输出功率为401.76 mW，可满足无线传感器或信号处理电路的用电需求。

图4 永磁体和感应线圈上的磁场有限元分析
Fig.4 Finite element analysis of magnetic field on the permanent magnets and the induction coils

图5 正弦振动激励下能量采集装置的输出电动势
Fig.5 Output electromotive force calculation value of energy harvester under sinusoidal vibration excitation

3 实验研究

为了验证所设计的两自由度电磁振动能量采集装置的效果，制作了振动能量采集装置样机，并在实验室的振动台上进行了测试。弹簧的刚度为10 N/mm，永磁体是长宽高分别为40 mm、20 mm和10 mm的长方体钕铁硼，9个定子线圈由线径0.25 mm的漆包线绕制，每个线圈匝数为400匝，间隔15°均匀分布在动子两侧，摆杆长度为80 mm。

采用加速度测试仪测得斯柯达轿车在城市道路行驶时的加速度a，并将该信号输入电动式振动台控制软件制成路谱信号(如图6所示)，通过振动台进行回放。将振动能量采集装置样机竖直固定在振动台台面上，通过示波器测量车辆线圈的输出电动势。测得的输出电动势如图7所示。

图6 电动式振动台回放的轿车加速度信号
Fig.6 The acceleration signal of a car played back by a electric vibration generator

图7 示波器测得的能量采集装置输出电动势
Fig.7 Electromotive force of energy harvester measured by an oscilloscope

在图7中，输出电动势最大峰峰值和有效值分别为18.63 V和8.47 V。振动能量采集装置的平均输出功率约为594 mW，可满足手机等小功率电子设备的供电需求。

4 结论

理论分析表明，在幅值20 mm、频率10 Hz的正弦振动激励下，本文提出的两自由度电磁式振动能量采集装置能够将直线振动位移放大约3倍，动子最大摆动角度接近80°。根据斯柯达轿车的实际道路振动加速度谱，将样机在振动台上进行了测试，产生的感应电动势有效值为8.47 V，平均输出功率约为594 mW。理论和实验分析表明，在直线振动激励的条件下，通过拾振机构将直线运动转换为旋转运动，可有效增加动子与定子的相对位移，有利于提高振动能量采集的发电功率。且在位移振动激励下，由于输入到转动机构的转矩较低，需尽可能降低电磁转矩，不宜采用传统发电机的磁路结构。