基于脉搏波特征参数的无创血红蛋白检测研究

甘永进，赵 地，陈 辉，李 琼，郑金存，*

(1. 玉林师范学院 物理与电信工程学院，广西 玉林 537000；2. 玉林师范学院 体育健康学院，广西 玉林 537000)

0 引言

作为体内负责运载氧的蛋白质，血红蛋白是血液的重要组成部分，是衡量贫血、失血以及真性血红蛋白增多症等疾病诊断和分类的重要指标[1-2]。当体内血红蛋白水平低于正常水平时表现为贫血，贫血可导致孕妇免疫力下降，引发早产、死胎等现象，对新生儿的器官、骨骼以及智力的发育也有不良影响[3]；而当体内血红蛋白水平高于正常水平时，常伴随着肿瘤、心肺疾病等疾病的病发[4]。因此，检测血红蛋白对相关疾病的及时诊断和预防至关重要。

目前对血红蛋白的检测主要通过有创的手段进行，不但对患者带来创伤，并且检测周期长、价格贵、需要专业的医护人士进行操作，不利于开展家庭或社区的检测工作，而无创血红蛋白检测方法可以避免上述问题，故对无创血红蛋白检测展开研究具有一定的现实意义。

本文采用双波长发光管对指尖光电容积脉搏波信号(Photoplethysmography，PPG)进行采集，结合集合经验模态分解(Ensemble Empirical Mode Decomposition，EEMD)及形态学滤波方法对PPG信号进行降噪处理后提取PPG信号形态、时域和频域的特征参数，再由皮尔森相关系数和主成分分析(Principal Component Analysis，PCA)对特征参数进行筛选，形成最优特征子集，最后由支持向量回归方法(Support Vector Regression，SVR)建立血红蛋白预测模型。

1 PPG采集系统的设计

功能性血红蛋白(氧化血红蛋白、还原血红蛋白)及非功能性血红蛋白(高铁血红蛋白、碳氧血红蛋白)构成了人体血红蛋白，前者约占人体总血红蛋白含量的95%～99%，故血红蛋白浓度检测常指检测功能性血红蛋白浓度。

本文基于修正后的朗伯-比尔定律进行无创血红蛋白检测研究，由两个波长的光源对指尖进行照射，得出物质浓度方程组并解出各物质的浓度。朗伯-比尔定律如式(1)所示：

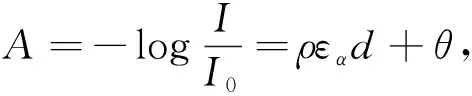
(1)

其中，ρ为路径长度因子，εα是吸光系数，d是最短路径，θ是未知集合因子，I0、I为入射前后的光强。

对式(1)两端进行求导得

(2)

其中，〈L〉是平均路径长度。由修正后的朗伯-比尔定律，得吸光度变化ΔA为

ΔA=[ε1(λ)c1+ε2(λ)c2+…+ε1(λ)c1]ΔL。

(3)

因本文主要检测氧化血红蛋白和还原血红蛋白两种蛋白的浓度，故选取两种波长进行这两种蛋白的检测，此时由式(3)可得

(4)

其中，ε1(λ1)和ε1(λ2)表示氧化血红蛋白在波长λ1、λ2处的消光系数，而ε2(λ1)和ε2(λ2)表示还原血红蛋白在波长λ1、λ2处的消光系数。由式(4)得

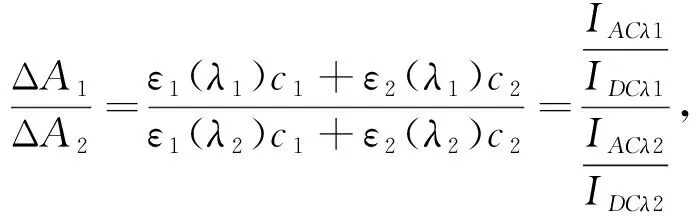
(5)

其中，c1、c2为分别为氧化血红蛋白和还原血红蛋白的浓度，IACλ1、IACλ2为两路PPG信号的交流分量，IDCλ1、IDCλ2为两路PPG信号的直流分量。因血氧饱和度Spo2为c1和c2的比值，结合式(5)可得

(6)

当λ2选择氧化血红蛋白和还原血红蛋白具有等吸收点的波长时，ε2(λ2)=ε1(λ2)，式(6)可简化为

(7)

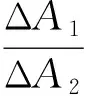
综上所述，因氧化血红蛋白和还原血红蛋白在某一给定波长处总的吸光量等于两者在该波长处各自吸光量之和，故选定两个波长的光源进行检测，可以组成一个二元一次方程组，由此解得氧化血红蛋白和还原血红蛋白的浓度。而选择等吸收点可以简化求解方程，由图1可见，由于在波长为905 nm处血红蛋白的消光系数变化比较平缓，且其值与等吸收点805nm波长处相差较小，可认为近似相等，因此λ2选择为905 nm。另外，为避免信号混叠，λ1尽可能选取两者吸收系数差异大的波长。图1中可见，660 nm波长处，两种血红蛋白吸收系数差别最大，故λ1选择为660 nm。本文使用660 nm和905 nm的光源分时复用分别描记PPG信号。

图1 两种蛋白的吸收特性
Fig.1 Absorption characteristics of two proteins

为采集到可靠的指尖光电脉搏波信号，本文采用集成了波长905 nm与660 nm的双波长反射式血氧传感器DCM03进行指尖PPG信号的检测。结合TI公司的完全集成模拟前端芯片AFE4400，由AFE4400控制DCM03双波长发光管交替开启的频率[5-7]，并完成I-V转换、光电信号矫正、滤除电路高频噪声以及AD转换等工作，完成对数字化指尖容积脉搏的采集，再将数字化脉搏波信号经过SPI接口传输给MCU(MSP430F5529)，在MCU里做进一步处理后传输给PC机。具体设计框图如图2所示。

图2 PPG采集系统框图
Fig.2 Block diagram of PPG acquisition system

2 EEMD结合形态学的降噪处理

受环境光、暗电流以及肌电等因素影响，系统采集到的原始PPG存在高频干扰及基线漂移等，波形如图3(a)所示。为提高PPG信噪比，得到更纯净、可靠的PPG信号以提升后续特征点识别的准确性，本文采用EEMD结合形态学滤波的方法对原始PPG信号进行降噪处理。

因为经验模态分解存在虚假分量和模态混叠的问题[8]，为提升分解效率[9]，采用更能提高信号信噪比[10]的EEMD对原始容积脉搏波信号进行处理。EEMD将信号分解得到的本征模函数(Intrinsic Mode Function, IMF)分量根据频率由高到低进行排列，信号中的噪声往往被分解到高频IMF分量中，EEMD降噪原理就是将高频噪声分量、虚假分量以及余项从原始信号中剔除，并对剩下的IMF分量进行重构，以恢复真实信号[11]，具体实现步骤如下：

① 对原始脉搏波信号x(t)添加白噪声ωi(t)，得到复合信号xi(t)=x(t)+ωi(t)；

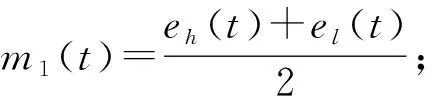
③xi(t)与m1(t)作差，得到去除低频信号的信号h1(t)=xi(t)-m1(t)；

⑤ 原始信号x(t)减去这个高频IMF分量，得到r1(t)=x(t)-c1(t)；

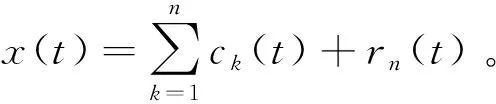
1.1.1 课程体系 目前该课程是电子科学与技术专业的选修课，为学生知识拓展，以及能力提升之用．集成电路设计设置在电子科学与技术专业大三第2学期，修完的专业基础课只有模拟电子电路、数字电子电路、电路分析、理论物理基础和半导体物理，对集成电路设计课程来说，还缺少必要的固体物理、晶体管物理以及量子力学．此外，也没有集成电路设计相关的专业课，如集成电路工艺、集成电路设计CAD、集成电路封装与测试等专业课．若没有集成电路专业基础课的学习，学生后续学习就比较吃力，教师讲授也相对较困难，也就是说，不管对教师教学，还是学生学习，都没有很好的知识体系框架的保障．

即原信号被分解为n个平稳信号和一个余项，将高频噪声分量、虚假分量以及余项从原始信号中剔除，并对剩下的IMF分量进行重构即可实现EEMD对脉搏波的降噪处理。

图3 各阶段PPG信号及其频谱图
Fig.3 The wave form and spectrogram of PPG

经EEMD滤波后的波形见图3(b)。对比图3(a)和(b)可见EEMD处理重构后的信号信噪比更高。但EEMD处理后的信号存在基线漂移，本文基于形态滤波，设计不同尺寸结构元素的开-闭和闭-开运算的平均对PPG的基线漂移进行抑制[12]。开运算可消除微小的尖刺，滤除信号峰值噪声，平滑信号边界轮廓，而闭运算用于实现平滑或抑制信号波谷噪声。传统形态的开-闭和闭-开运算以不同顺序级联开闭运算存在统计偏移现象，为避免该现象，定义广义开-闭和闭-开滤波器为

FOC(f,g1,g2)=f○g1●g2，

(8)

FCO(f,g1,g2)=f●g1○g2，

(9)

其中，FOC和FCO分别代表广义开-闭运算和广义闭-开运算，g1和g2表示不同尺寸的结构元素，f代表欲进行基线漂移抑制的信号，○和●分别代表开运算和闭运算。

具体步骤框图见图4，将EEMD重构后的信号分别和不同结构元素进行开-闭和闭-开运算后，将两者的结果进行平均，再与输入信号相减得到抑制漂移的信号。经过形态学滤波后的波形见图3(c)，结合图5各个阶段波形的频谱可见，基线漂移得到了抑制，信号比得到了提高。

图4 去基线漂移框图
Fig.4 The block diagram of baseline removal

图5 各个阶段波形的频谱图
Fig.5 spectrogram of each stage

为进一步说明算法的有效性，本文比较不同小波算法、传统陷波器以及本文算法对PPG信号处理后的信噪比，实验结果如表1所示。由表1可见，本文算法得到的信噪比较高，在对系统采集到的原始PPG信号进行处理时，效果优于小波及传统陷波器。

表1 几种不同去基线算法的信噪比
Tab.1 SNR of different algorithms

3 PPG特征参数的提取与筛选

3.1 PPG特征参数的提取

经EEMD和形态学滤波共同处理降噪后的PPG信号可进行特征提取工作。本文主要对PPG信号进行形态特征、时域特征参数以及频域特征参数的提取。

参数提取操作以一个周期PPG为对象，采用数据分割与区间搜索提取算法，定义并选择其原波形及一阶微分、二阶微分波形的特征信息，提取波形关于时间信息、幅值信息、比值信息、面积信息、频域信息等具代表性的特征参数。首先，在一个完整周期内的PPG波形及其一阶微分、二阶微分波形上搜索PPG波峰、PPG波谷、波潮、重搏波峰、重搏波谷、主波一次微分波形峰值点、重搏波一次微分波形峰值点、潮波一次微分波形波谷点、主波二次微分波形波峰点、二次微分波形波谷以及潮波二次微分波形波峰等特征点，在此基础上计算相应特征点的幅值，并计算时间信息参数诸如血流射出加速度最大时间段、一次心跳周期时间段、脉搏传播时间[13]、血流射出容量最大时间段等，计算比值信息参数诸如潮波与主波的幅值比、重搏波峰与主波的幅值比、重搏波谷与主波的幅值比等，计算面积信息参数诸如一个完整周期内PPG波形的面积、信号起始点至潮波处的面积、潮波至重搏波谷处的面积以及重搏波谷下一个信号起始点的面积等，计算频域信息参数如频谱峰值最大、次大频率点等，加上年龄、身高、体重等个人信息参数，形成一个包括32个特征参数的集合。

实验中，将采取的一分钟内多个周期的信号进行上述特征参数的提取得到多组特征参数，再计算每个特征参数[14]的平均值以形成特征参数向量，最后将各特征参数从1至32进行编号组成含32个特征向量的原始特征向量集。

3.2 PPG特征参数的筛选

皮尔森相关系数反映两个变量间的相关性，两个变量间的皮尔森相关系数绝对值小于0.2时说明这两个变量间不具备相关性，反之则具有相关性。PCA算法将一个矩阵中的样本数据投影到一个新的空间中去，包含了原始特征的绝大部分信息[15]的同时去除冗余的属性特征，实现特征空间降维。

为去除冗余及不相关的特征及达到降低维度的目的，在不影响精度的前提下提高算法效率，本文通过由皮尔森相关系数先排除掉不相关的特征参数，再由PCA进行降维，去除冗余的特征，保留核心特征并完成高维空间映射到低维空间，最终形成核心特征子集。

实验时，对200个测试者进行实验，采集到200个测试者的PPG信号并进行降噪处理后，提取特征参数得到200×32大小的特征矩阵，结合每个测试者的血红蛋白值进行相关性分析得到皮尔森相关系数如图6所示。

图6 皮尔森相关系数图
Fig.6 Pearson correlation coefficient

由图6知，有21个特征参数皮尔森系数在0.2以上，故可构造出用于计算血红蛋白的矩阵大小为200×21，对该矩阵进行主成分分析，得到该矩阵主成分的特征值，如图7所示。选择特征值大于1的主成分，因此可得到11维用于计算血红蛋白的矩阵。

图7 各主成分的特征值
Fig.7 Characteristic value of principal component

其中，被选择用于后续建模的11个特征分量别是血流射出加速度最大时间段、射血结束时间段、脉搏传播时间、PPG起始点到潮波处的面积、PPG射血加速度最大处的幅值与PPG波峰幅值的比、潮波二次微分波形波峰对应PPG波形处的幅值与PPG波峰幅值的比、潮波一次微分波形波谷对应PPG波形处的幅值与PPG波峰幅值的比、收缩期与舒张期射血速度最大时间段、一次心跳周期时间段、对应二次微分峰值的PPG波形处的幅值以及PPG起始点到重波峰值的时间段。

4 SVR模型对血红蛋白的预测

作为一种以核思想为基础的模型训练方法，SVR不仅减小算法结构风险，而且克服传统预测算法中模式识别的缺陷，其使用内积核函数定义的非线性变换把输入空间转换到另一个高维空间，在这个高维空间里求解最优超平面[16]。SVR可简述如下：

对于训练样本集T，T={(x1,y1),(x2,y2),…,(x1,y1)}∈(x×y)l，其中xi∈Rm,yi∈{-1,1},i=1,…,l，则上述提到的11维矩阵可组成本文的训练样本集，形如y=ω1x1+ω2x2+…+ωNxN，简化为f(x)=ωTx+b，求解最优化问题，其优化目标函数为

s.t.yi((ω·xi)+b)≥1。

(10)

根据最优解(ω·x)+b*=0确定的分类面，决策函数为f(x)=sgn((ω·x)+b*)。

推广至回归问题即SVR，引入损失函数，构造最小化目标如下：

(11)

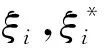
综合考虑非线性因素及降低模型复杂度，本文在选择RBF作为核函数的前提下，为建立稳健的SVR模型，本文基于交叉验证理论的网格搜索方法优选惩罚参数c与核函数参数g。

实验进行时，对30个男性与20个女性进行数据的采集，测试者的年龄在18～55周岁之间。测试者经过适当休息后，保持身体平稳避免抖动，同时使用本系统与Mission Hb微创血红蛋白分析仪进行实验。本系统采集到的数据作为预测值，而Mission Hb微创血红蛋白分析仪测量得到的数据作为真实值，两者相关性分析如图8所示，图中虚线为y=x。

经实验得，预测值和真实值之间的相关系数为0.76，表明基于SVR的人体血红蛋白含量的无创检测有一定的可靠性，与临床检测方法的检测具有较高的相关性。

图8 数据相关性分析
Fig.8 Correlation analysis

为进一步说明所建模型的有效性，对实验数据进行一致性校验，得到测值与真值之间的P值为0.802 4，H值为1。由两组数据绘制的盒子图如图9所示，从图9可见，盒子的本体有重叠部分，说明两组数据没有显著性差异。

为说明本文方法处理效果的优越性，对上文50个测试者采集到的11维数据集，将SVR模型与其他常用模型分别进行处理并预测血红蛋白值，结合实际的有创测量结果并计算预测相关系数(Relevant coefficient of prediction，Rp)、预测标准偏差(Root mean squared error of prediction，RMSEP)，结果如表2所示。Rp反映真值和测值之间相关的程度，而RMSEP衡量数据值偏离算术平均值的程度，由表2可见，相比多项式回归、偏最小二乘回归以及kNN算法，本文算法在具有最高的相关系数，而预测标准偏差最小，说明本算法相比于这几种常用的算法而言，预测效果最佳。

图9 两组数据的盒子图
Fig.9 Boxplot of two sets of data

表2 SVR与常用算法处理效果的比较
Tab.2 Comparison of SVR and common algorithms

4 结论

结合DCM03与AFE4400设计光电容积脉搏波采集系统以开展人体血红蛋白的无创检测研究。设计EEMD结合形态学滤波的方法对PPG信号进行降噪，通过对比不同滤波方法的信噪比，发现本文方法滤波效果较好，优于小波算法及传统陷波器。为验证血红蛋白预测模型的有效性，对50位实验者进行测量，实验结果表明，相关系数达到0.76，测值与真值之间有较高的相关性。为进一步说明模型的可靠性，对测值与真值进行一致性校验，得到两者间P值为0.802 4，H值为1，两者盒子图本体有较大重叠，表明测值与真值之间没有显著性差异。为说明本文方法的优越性，将SVR与多项式回归、偏最小二乘回归以及kNN这几种常用算法进行对比，由相关系数及标准偏差可知，SVR预测效果最佳。实验结果表明，论文建立的无创血红蛋白检测模型具有一定的可靠性和准确性，可望用于贫血症早期诊断。