连续退火过程带钢板形演变模型及其应用研究

王晓雷，何召龙，许 鹏，王云祥，白振华,2,*

(1. 燕山大学 国家冷轧板带装备及工艺工程技术研究中心，河北 秦皇岛 066004；2. 燕山大学 亚稳材料制备技术与科学国家重点实验室，河北 秦皇岛 066004)

0 引言

近年来，随着板带用途逐渐从中低端转向高端，用户对板带产品的质量要求越来越高。而经过冷轧后的钢板无法直接进行冲压等成型加工，必须经过退火工序使其形核、再结晶以达到减少晶格缺陷、利于进一步深加工的目的。与此同时，经过连退工序后的冷轧带钢不仅性能会发生改变，其板形也会发生变化。连退机组的出口板形就是平整机组的入口板形，其板形形态直接影响到成品带钢的板形质量。以往对于连退工艺的研究主要集中于产品性能[1-3]与通板的稳定[4-8]问题，同时将冷轧出口板形作为连退平整的入口板形，而忽略连退工序对板形的影响，导致成品带钢的板形精度欠佳。这样，如何确定带钢在连退工序板形的演变规律，对连退过程中的板形进行快速预报，最终实现连退工序板形有意识地控制就成为现场技术攻关的焦点，本文即在此背景下围绕连退过程中的板形问题而展开。

1 连续退火过程带钢板形演变机理

在连退过程中，炉内不均匀因素(如带材跑偏、炉辊辊型、带钢横向温度差、炉辊安装误差等)都可能会使带钢内部张应力沿着横向重新分布，板形也会随之发生改变。在这一过程中，倘若重新分布后的横向张应力分布没有使得相应部位发生局部的塑性变形，此时带钢内部沿着横向板形的变化可以认为仅仅发生在该特定单元内，而不会对下一个单元产生任何实质性的影响，随着退火的进行，当带材离开该单元进入下一单元之后板形将迅速恢复到原始来料状态，不会存在任何残留；反过来说，如果张应力沿着横向重新分布后带钢局部出现了塑性变形，此时带钢内部板形的改变将不仅仅体现在当前单元之中，还会影响到该单元的出口板形甚至成品带钢的板形，并且带钢的板形在单元内与单元出口处是不同的。单元内的板形是酸轧来料板形与连退炉内不均匀因素而引起的板形相互叠加的结果；而单元出口的板形则是酸轧来料板形与连退炉内带材局部塑性变形而引起的板形相互叠加的结果。为了方便表达，可以将单元内的板形用“单元内板形”来表示，而将单元出口的板形用“单元外板形”来表示。其中，单元内板形可以认为主要影响的是本单元的稳定通板，而单元外板形则作为下一单元的来料板形影响下游单元的单元内板形、稳定通板，单元外板形甚至影响机组的最终成品板形。

2 连续退火过程带钢板形模型

2.1 带钢横向张应力分布模型

对于连续退火过程中带钢内部张应力的横向分布问题，白振华[9]和王瑞[10]对连退过程中稳定通板进行过相应研究。其中王瑞将带钢沿着宽度方向分条，进而采用条元法建立了连退过程中带钢内部张应力横向分布的模型，计算出了相应的连退过程中带钢内部张应力的横向分布。由于王瑞建立连退过程中带钢内部张应力横向分布模型的目的是研究热瓢曲与跑偏问题，因此尽管离散法割裂了条元之间的联系与条元互相之间的约束关系，但计算精度对分析热瓢曲及跑偏问题的影响并不是很大。然而，如果在计算连退过程中炉内及炉外板形问题时仍采用离散法，割裂条元之间的约束，则会带来较大的计算误差。同时，王瑞博士更注重于特定单元带钢内部张应力横向分布的影响，而对于单元间的互相作用与耦合没有考虑。为此，经过大量的理论研究与现场试验跟踪，充分考虑到来料板形与炉内不均匀因素(如带材跑偏、炉辊辊型、带钢横向温度差、炉辊安装误差等)的影响，并结合连退机组的设备与工艺特点，将带材沿着横向按照一个有机的整体进行处理，并且兼顾上下单元之间板形的相互影响，建立了一套连退过程带钢内部张应力横向分布模型。

2.1.1带钢内部张应力横向分布模型

为了建立连退过程中带钢内部张应力的横向分布模型，如图1所示，可将整个连退炉从预热段开始，将预热段、加热段、均热段、缓冷段、快冷段、时效段以及终冷段按照炉辊对数分成N个研究单元，并取任意第i个单元进行研究。如图2所示，在研究过程中每个研究单元都以上炉辊的上母线作为起始线(如图2中的直线AA′)、下炉辊的下母线作为终点线(图2中的DD′)。于是，对于特定的带钢单元来说，其沿着纵向可以认为是由带钢与上炉辊相互接触部分(图2中AA′BB′)、上下炉辊之间的部分(图2中BB′CC′)以及带钢与下炉辊相互接触部分(图2中CC′DD′)三部分组成。根据连退炉的结构特征可以知道，沿着纵向AA′BB′、CC′DD′部分带钢的长度要远小于BB′CC′部分带钢的长度，因此虽然由于带钢与炉辊之间摩擦力的存在，AA′BB′、CC′DD′部分张应力沿着纵向会发生细微的变化，但在模型的建立过程中可以将这部分张应力的变化予以忽略，也就是说建模过程中在单元内纵向上可以用平均张应力替代纵向各点张应力，即认为单元内张应力沿着纵向是不变的。

图1 连退过程中带钢划分单元示意图
Fig.1 Schematic diagram of strip dividing unit during continuous annealing

通过以上叙述，如果以炉辊中心作为原点建立坐标系，以工作侧为正、传动侧为负，就可以将连退过程中带钢内部张应力横向分布模型用高次曲线来表示:

(1)

式中，σi(x)为第i个单元内带钢张应力横向分布值(MPa)；x为横向坐标值；m为张应力分布高次项的最高次数，一般m=4或者m=6；aik为第i个单元内带钢张应力横向分布特征参数；k为过程参数；B为带材宽度(mm)。

图2 带钢沿宽度划分单元示意图
Fig.2 Schematic diagram of strip steel dividing unit along the width direction

通过式(1)可以知道，对于一个特定的连退过程的特定单元而言，只要带钢张应力横向分布特征参数aik确定了，那么单元内带钢张应力的横向分布值也就确定了。

2.1.2带钢张应力横向分布特征参数的求解

在连退过程中对于特定单元的带材而言，不管内部张应力在横向如何分布，其平均值必须与张应力设定值相等，可以表示为

(2)

如果去掉平均值，用Δσi(x)来定义残余应力，则Δσi(x)可以表示为

(3)

将式(1)～(2)代入式(3)并整理，又可以将残余应力Δσi(x)表示为

(4)

显然，对于式(4)而言，只要第i个单元内带钢张应力横向分布特征参数aik确定，那么残余应力Δσi(x)就确定了。

与此同时，在连退过程中，带钢内部之所以会出现残余应力Δσi(x)，其主要根源在于来料板形、带钢横向温差、炉辊辊型以及炉辊安装误差4个方面，现分述之：

1) 来料板形引起的残余应力

所谓的来料板形(即上一单元的单元外板形)引起的残余应力，可以表示为

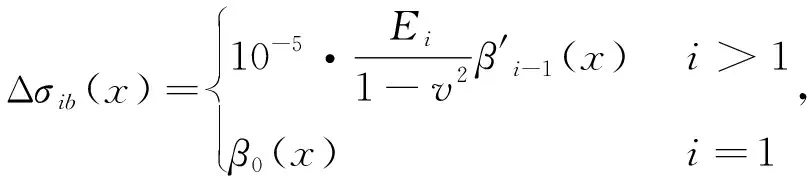
(5)

(6)

式中，b0k为酸轧来料板形系数。

2) 横向温度差引起的残余应力

在连续退火过程中，在任意第i个单元内带钢沿着横向温度分布Ti(x)可以简单表示为

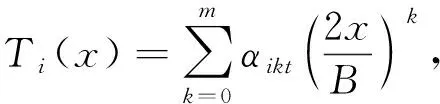
(7)

式中，αikt为温度特性系数。

相应地，第i个单元内带钢横向平均温度则可以表示为

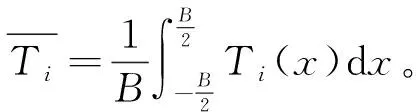
(8)

这样，第i个单元内带钢横向温差分布值ΔTi(x)则可以表示为

(9)

进一步地，将式(7)、(8)代入式(9)并整理，可将第i个单元内带钢横向温差分布值ΔTi(x)表示为

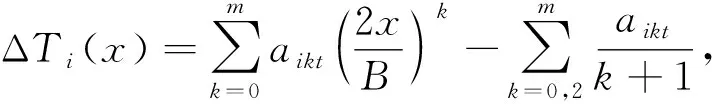
(10)

这样，由横向温差而引起的的残余应力Δσit(x)就可以表示为

(11)

式中，β为带钢线膨胀系数(℃-1)。

3) 炉辊辊型引起的残余应力

在连续退火过程中，任意第i个单元的炉辊包括上炉辊与下炉辊两个辊子，炉辊原始辊型、炉辊磨损辊型、炉辊热辊型分别可以分别表示为

(12)

(13)

(14)

式中，Dysi(x)、Dyxi(x)分别为上、下炉辊的原始辊型曲线；αysik(x)、αyxik(x)分别为上、下炉辊原始辊型曲线特性系数；Dmsi(x)、Dmxi(x)分别为上、下炉辊炉辊磨损曲线；αmsik(x)、αmxik(x)分别为上、下炉辊的炉辊磨损曲线特性系数Drsi(x)、Drxi(x)分别为上、下炉辊热辊型曲线；αrsik(x)、αrxik(x)、分别为上、下炉辊热辊型曲线特性系数；Li为第i个单元炉辊的辊身长度(mm)。

将式(12)～(14)综合可以得到连退机组第i个单元上下炉辊的实际辊型曲线

(15)

式中，Dssi(x)、Dsxi(x)分别为上、下炉辊的实际辊型曲线。

这样，由于炉辊实际辊型曲线的存在而引起炉辊在与带材接触部位的辊径差为

(16)

对于上、下炉辊在带材接触处的平均辊径则可以表示为

(17)

综合式(12)～(17)，并积分整理即可得到炉辊实际辊型曲线与带钢接触部位的辊径差的具体表达式

(18)

假设带钢与炉辊的包角为180°，那么由于炉辊实际辊型曲线在与带材接触部位的辊径差而引起的第i个单元带材在长度方面的差值就可以表示为

(19)

式中，Δlgi(x)为辊径差而引起的第i个单元带材在长度方面的差值(mm)。

与之对应，炉辊辊型引起的残余应力则可以表示为

(20)

式中，ΔσiD(x)为炉辊辊型引起的残余应力(MPa)；Hi为第i个单元内上、下炉辊中心线之间的距离(mm)；Ri为第i个单元内炉辊半径(mm)。

4) 炉辊安装误差引起的残余应力

当炉辊因为加工、安装等原因出现垂直方向或者水平方向误差时，也会导致带钢内部在横向出现残余应力。假设上、下炉辊在垂直度方向总的误差为Δci，水平度方向总的误差为Δsi，那么因为垂直度及水平度误差而引起的第i个单元带材在长度方面的差异Δlci(x)、Δlsi(x)分别可以表示为

(21)

(22)

这样，与之对应，因炉辊加工及安装误差引起的残余应力Δσiw(x)可以表示为

(23)

这样，综上可以从几何方面求出相应的连退过程中带材内部残余应力横向分布值

Δσgi(x)=Δσib(x)+Δσit(x)+

ΔσiD(x)+Δσiw(x)，

(24)

比较式(24)及式(5)，并构造一个目标函数

(25)

其中，X={aik}。

这样，求解第i个单元内带钢张应力横向分布特征参数aik的问题就可以转换为：寻找一个最佳的X={aik}，使得目标函数F(X)最小。采用Powell优化法[12]对一个多目标函数寻优得出结果。

2.1.3张应力横向分布特征参数模型的修正

实际上，进一步分析可以知道，式(24)成立的条件是连退过程中带材所有单元都没有发生塑性变形。如果带材在横向某些部位发生了塑性变形，那么式(24)就必须进行修正。修正方法如下：

Δσgi(x)=Δσib(x)+Δσit(x)+ΔσiD(x)+

(26)

同时修正后的第i单元连退过程中带材内部残余应力横向分布值为

(27)

式中,σsi为第i单元带材的屈服强度值(MPa)。

2.2 单元内板形模型

对于特定单元而言，在求得带材内部残余应力横向分布值之后，其板形值为

(28)

需要说明的是，此时带材表现出来的板形并不是带材的实际板形，而是涵盖了温差、辊型、炉辊安装误差等因素的表观板形，这些因素会随着带材走出该单元而发生变化。而扣除上述因素影响之后的板形才是此段的实际板形，即所谓的单元外板形。

2.3 单元外板形模型

实际上，在连退过程中对于任意第i单元内的带材而言，由于来料板形、带钢横向温差、炉辊辊型以及炉辊安装误差4个方面因素而引起的带材横向变形差是始终存在的。为了抵消这种变形差，带材内部会出现应力分布的不一样，从而出现弹性变形的不一样，但如果某部位的弹性变形不足以弥补这种几何变形差时，带材将会发生塑性变形，以弥补这种变形差。在此原理下，可以将任意第单元内的塑性应变表示为

(29)

当带材走出第i单元之后，炉辊辊型、炉辊安装位置误差、带钢横向温差引起的变形会消失，带材内部应力会重新分布，局部有可能会再次发生塑性变形，此时的板形就是所谓的单元外板形。计算方法如下：首先，假设应力重新分布后不发生塑性变形，那么带材经过第单元之后的附加应力为

(30)

考虑到来料的板形，此时实际残余应力分布Δσis(x)可以表示为

Δσis(x)=Δσif(x)+Δσib(x)，

(31)

此时单元外板形可以表示为

(32)

Δσis(x)=Δσif(x)+Δσib(x)+

(33)

同时修正后的第i单元连退过程中带材内部残余应力横向分布值为

Δσis(x)′=

(34)

最后，根据连退炉内的带钢板形模型及其演变机理可知，任一工艺段参数的设定对板形的影响体现在单元内板形和单元外板形两个方面，而单元外板形作为下一工艺段的来料板形又将影响后续工艺段。由此可知，从来料板形到最终出口板形，塑性变形既具有遗传性，又具有演变性。因此，实现出口板形控制的前提是建立连续退火炉段的板形控制思想，分析板形的逐段演变规律。

3 模型应用

某1550连续退火机组为监控机组连退过程中带钢通板的稳定性，同时跟踪带钢在炉内运行过程中及单元外板形情况，实现连退机组板形的有意识控制，结合该机组的设备和生产工艺特点，利用本文所述的板形模型，开发了一套连退机组板形在线显示软件，带钢在连退炉出口的板形情况如图3所示。

图3 连退机组出口板形预报软件主界面
Fig.3 Main interface of export plate forecast software for continuous annealing unit

为了进一步地分析连退机组板形模型的预报精度，特选1550连退机组(全炉段主要设备及工艺参数如表1所示)的典型规格产品进行现场试验，在试验中板形的实际测量值采用抬起平整机的轧辊不平整而后取样的方法，有关产品规格及钢种见表2，板形的模型预报值与实际测量值的对比如图4所示。

表1 连退炉全炉段相关工艺及设备参数
Tab.1 Process and equipment parameters of the whole furnace section of continuous annealing furnace

设定张应力MPa温度℃辊径mm平直段mm凸度mm预热段9120～1509002503加热段7.57609004502均热段7.57609006000.4缓冷段8.5600～7001 300——快冷段114501 6004500.5时效段124001 6004500.5终冷段14.5<2001 6004500.5

表2 实验产品基本特性参数
Tab.2 Basic characteristic parameters of experimental product

产品号钢种规格/mm1CQ1 250×0.72DQ1 120×0.83EDDQ1 320×0.64DDQ1 200×0.5

通过图4及表3可以看出，采用本文所述模型得到的连退板形预报值与实测值误差在15%内，且趋势完全一致，可以满足工程上对板形的预报需求。

图4 典型规格产品板形预报值与实测值对比
Fig.4 Comparison of plate shape prediction values and measured values of typical specifications

表3 实验产品板形值结果及误差
Tab.3 Shape value results and error of experimental product

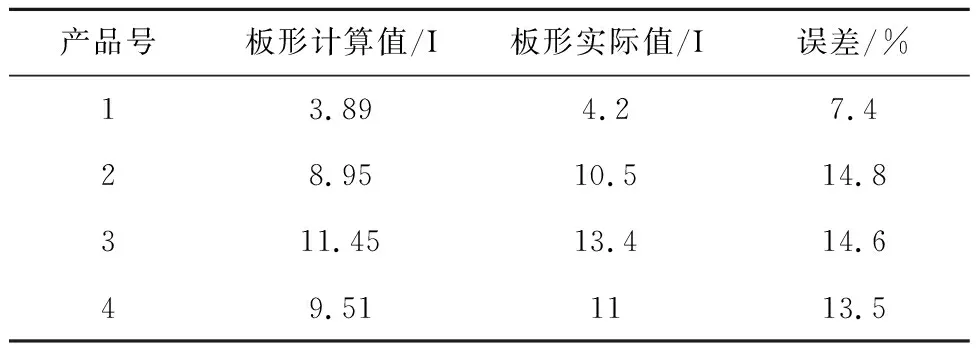
产品号板形计算值/I板形实际值/I误差/%13.894.27.428.9510.514.8311.4513.414.649.511113.5

4 结论

1) 不同于以往对连退工艺的研究仅关注于性能和稳定通板，本文从板形的角度结合连退机组的设备与工艺特点，并考虑炉辊原始辊型、来料板形、横向温差以及炉辊水平方向与垂直方向误差等因素对连续退火过程带钢板形的影响，还兼顾到上下单元之间板形的相互影响，最终建立了一套适合于连续退火过程的带钢内部应力横向分布模型。

2) 从连退过程中炉内带钢的塑性变形问题入手分单元内及单元外两种不同工况分别建立连退炉内板形模型，建立的模型可以逐单元完成对炉内带钢在各个单元的板形演变规律的分析，在生产中有重要的参考价值。

3) 相关连退板形模型被推广应用到生产实际，误差可以控制到15%以内，且趋势完全一致，可以满足工程上对板形的预报需求，具有进一步推广应用的价值。