飞机蒙皮锤铆参数优化方法研究*

鲁墨武，殷思羽，姜春英，康玉祥

(沈阳航空航天大学 机电工程学院，辽宁 沈阳 110136)

0 引言

飞机装配技术中，飞机蒙皮装配大多采用铆接连接方式，因此提高铆接质量是航空制造技术必然的发展趋势。在现代飞机铆接技术中，通常采用人工锤铆，受铆接件结构的约束，一般采用反铆法[1]。

目前针对铆接工艺的研究，主要集中在铆接工艺参数的选择与优化。DeRijck等[2]研究了压铆力和镦头尺寸之间的关系， Cheraghi等[3]研究了铆接工艺参数对铆接质量的影响，陈彦海等[4]研究了铆枪输入气压和锤铆时间与铆钉镦头尺寸的关系。经查阅大量文献发现：国内外学者对影响铆接质量的工艺参数做了大量的研究，然而对铆接工艺参数多目标优化方面还少有研究。本文针对双机器人自动反铆设备进行研究，结合ABAQUS软件，基于BP神经网络的适应度函数，采用PSO算法进行工艺参数优化，并进行了仿真和实验验证。

1 ABAQUS仿真获得样本数据

通过自动锤铆工艺分析，本文对飞机蒙皮自动锤铆系统进行简化[5]，如图1所示，自动反铆过程中活塞受气压p的作用，以速度v0撞击铆枪冲锤，冲锤受力锤打铆钉头，同时顶铁顶住铆钉杆并以一定的速度向铆枪方向移动一定的距离。

图1 自动反铆系统

本文采用ABAQUS/Explicit求解器，建立有限元分析模型，如图2所示，并使用Python语言对ABAQUS软件进行二次开发，建立锤铆循环仿真程序,详见文献[4]。

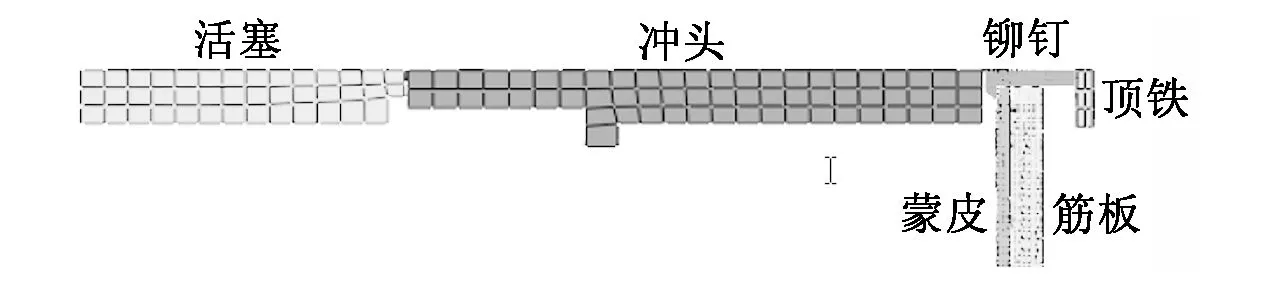
图2 有限元仿真模型

由于锤铆力由铆枪输入气压p决定，因此，根据以上仿真分析模型，以铆枪输入气压p、铆钉头内端面到蒙皮间距l、冲锤次数i为输入参数进行有限元分析。根据文献[6]可知，工艺试验用到的铆枪在不同气压下获得其相对的瞬时锤铆力和活塞速度，如表1所示。

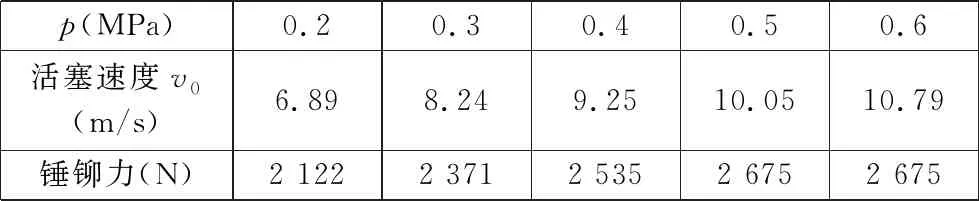
表1 不同气压下铆钉瞬时锤铆力和活塞速度

采用表1所示的输入气压，对有限元模型进行分析。气压为0.5 MPa，铆钉头内端面到蒙皮间距离为0 mm时，不同冲击次数i下的局部铆钉蒙皮变形图如图3所示。最终获得60组数据，部分数据如表2所示。表2中,D为铆钉头直径，Δ为蒙皮翘曲间隙。以这60组数据作为参数优化的样本数据。

2 工艺参数优化

将仿真分析获得的60组数据作为工艺参数优化的样本数据，构建基于BP神经网络的适应度函数，采用粒子群优化算法(Particle Swarm Optimization，PSO)对铆接工艺参数进行优化。

2.1 BP适应度函数建立

本文以铆钉头直径D和蒙皮翘曲间隙Δ为铆接质量评价指标，按照航空工业标准HB-Z2233-2003《飞机装配工艺》，镦头的尺寸要求如式(1)和式(2)所示：

D=(1.5±0.1)d.

(1)

H=0.4d.

(2)

其中：H为铆钉镦头高度的最小允许值；d为铆钉直径。通过计算和查找相关资料得出本文铆接质量标准如式(3)所示：

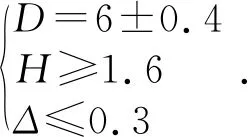
(3)

公式(3)表明：D越接近6 mm，且Δ越小，铆接效果越好，质量越高。

图3 不同冲击次数i时的蒙皮、铆钉变形图

表2 部分仿真分析结果

通过前文的分析，建立了D和Δ关于其影响因素(铆枪输入气压p、冲锤次数i、铆钉头内端面到蒙皮间距离l)的函数关系如下：

D(x)=f1(p,i,l).

(4)

Δ(x)=f2(p,i,l).

(5)

铆接工艺参数优化的过程可视为公式(4)和公式(5)同步优化求解的过程，因此，根据质量评价指标设计如式(6)所示的目标优化函数：

F(x)=min((D-6)2+Δ2)2.

(6)

式(6)为多变量非线性函数，很难找到具体的数学函数模型对其进行分析。因此，借助BP神经网络的非线性数据拟合能力，建立以铆枪输入气压p、冲锤次数i、铆钉头内端面到蒙皮间距离l为输入，以公式(6)优化目标所计算的结果为输出的网络模型，对所仿真的样本数据进行训练。

本文选取3层BP神经网络对样本数据进行训练，其中输入层、中间层、输出层的神经元个数分别为3、10、1。学习率为0.1。在60组样本数据中，随机选取50组进行训练，其余10组样本对结果进行验证，验证结果如图4所示，图4中各点处为预测值和实际值。图5为BP神经网络的预测误差分析图，结果显示预测相对误差在±0.8%的范围内，说明拟合精度较高，效果较好，满足本文要求。

2.2 PSO优化算法

PSO算法是一种基于种群的随机搜索算法，具有操作简单、搜索效率高和收敛速度快等优点[7]。

PSO算法采用一群粒子对应优化问题的解，每个粒子的特征用速度、位置和适应度三个指标表示。粒子通过更新自身的速度和位置来搜索求解空间中适应度最优的位置，从而实现最优解的全局搜索[8]。

图4BP神经网络预测结果图5BP神经网络预测误差

PSO算法优化流程如图6所示。

图 6 PSO算法优化流程图

以所训练的BP神经网络模型为PSO算法适应度的函数，对式(6)进行优化求解。选择PSO算法的训练次数为100次， 训练适应度值如图7所示，迭代20次即达到最优。铆接优化后，铆枪输入气压、冲锤次数、铆钉头内端面到蒙皮间距离分别为0.4 MPa、36次和0.1 mm。应用优化结果，得其仿真后的优化模型如图8所示，镦头直径D为6.003 mm，高度H为1.775 mm，蒙皮与筋板间最大间隙Δ为0.166 mm。

根据公式(3)，采用优化获得的仿真结果与理论值相比较，镦头直径D误差为0.003 mm，铆钉镦头高度H大于最小值，蒙皮到筋板间间隙Δ小于最大允许值。因此，表明PSO算法优化获得的最优工艺参数满足工艺要求。

3 锤铆实验

3.1 双机器人锤铆实验

锤铆实验在双机器人自动铆接实验平台上进行，该实验平台由两个对称形式的三自由度移动机器人组成。一台机器人的末端设置顶铁，顶住铆钉杆，另一台机器人末端设置铆枪，双机器人协调工作，可实现平面自动铆接功能。

3.2 实验结果及分析

通过调节调压阀，将铆枪的输入气压调整为0.4 MPa,根据0.4 MPa时铆枪的冲击频率，设置铆枪的冲击时间为1.49 s，冲锤冲击次数达36次。由于仿真及实验用筋板厚度为4.5 mm，蒙皮厚度为1 mm，铆钉杆长度为10 mm，上文对最优工艺参数仿真获得的铆钉镦头高度H为1.775 mm，表明铆钉杆形成镦头后长度减小了2.725 mm，因此，设置顶铁移动距离为2.7 mm，铆钉头内端面到蒙皮间距离l为0 mm。进行锤铆实验，共锤铆10个铆钉，图9和图10为铆钉和蒙皮的变形图。

使用三坐标测量仪对铆钉镦头直径D和高度H进行测量；使用激光位移传感器选取多点对铆钉头周围蒙皮凸出距离进行测量，取最大测量值。实验测量结果如表3所示。

图7 函数适应度曲线

图8 锤铆局部仿真变形模型

图9 铆钉镦头变形

图10 铆接蒙皮变形

测得10组铆钉镦头平均直径为6.098 mm，平均高度为1.842 mm。蒙皮的平均最大凸出量为0.182 mm。对比铆钉镦头实验值与仿真值得出：铆钉直径绝对误差为0.095 mm, 高度绝对误差为0.067 mm，蒙皮最

大凸出量的绝对误差为0.016 mm,三者误差均不大，铆钉镦头尺寸达到变形要求，铆接合格。实验结果验证了优化模型的有效性。

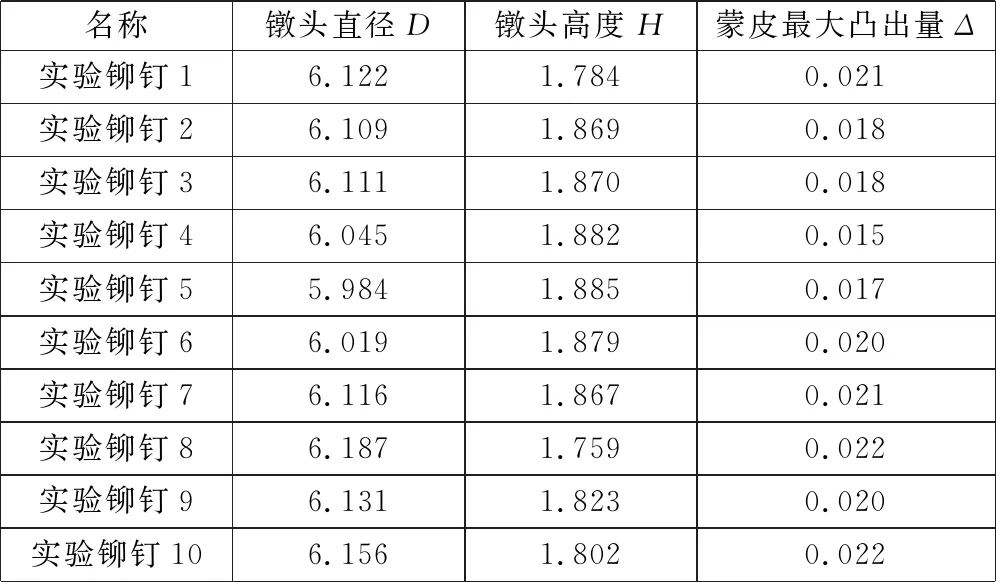
表3 实验测量结果 mm

4 结论

建立了基于BP神经网络的适应度函数，采用PSO算法，对ABAQUS仿真分析获得的60组样本数据进行参数优化，获得了最优工艺参数。基于双机器人锤铆实验平台进行锤铆实验，验证了优化的工艺参数能够实现较好的铆接质量，可为锤铆工艺参数优化提供一种新的思路，具有一定的推广价值。