基于响应面法的BaJa赛车车架轻量化设计与研究*

鲁春艳

(苏州市职业大学 机电工程学院 ,江苏 苏州 215000)

0 引言

中国汽车工程学会主办的巴哈大赛(简称BSC大赛)是面向高等院校开展的小型越野车比赛。大赛要求每支车队使用组委会指定的发动机，设计并制造一辆单座、发动机中置、后驱的小型越野车，并且要求所制造的赛车在加速性能、牵引能力、操控性能以及可靠性等方面具有良好的表现，以便在多个项目的竞赛中取得好成绩。

车架是汽车的承载基体，需具有足够的强度和刚度以承受汽车的载荷和从车轮传来的冲击，同时轻量化的车架可提高汽车的动力性，减少燃油消耗。因此，在保证车架强度、刚度及可靠性的前提下，需尽可能地减少车架的质量。本文在对车架进行有限元分析的基础上，根据分析所获得的数据，基于响应面法对车架进行轻量化设计，得到满足条件的质量更轻的车架。

1 赛车车架的设计

巴哈赛车多采用桁架式金属车架，一般由钢管焊接而成，在选材时以力学性能为主兼顾材料的焊接性能，选择30CrMo，其泊松比为0.279，弹性模量为211 GPa，密度为7 850 kg/m3。根据大赛规则确定车架的基本布局和尺寸，以满足载荷分配合理、有足够的承载能力、良好的人机工程性能及轻量化的要求，设计的车架模型如图1所示。本车架采用两种型号的钢管，图1中深色钢管为主要结构件，直径为31.75 mm，壁厚为1.8 mm；浅色钢管为次要结构件，直径为25.4 mm，壁厚为1.5 mm。

2 车架的强度分析

为了验证车架的强度性能，须对车架在各种工况下承受的最大载荷进行分析。在比赛过程中一般会出现以下五种工况：①弯曲工况，赛车在静止或者匀速行驶时因承受载荷而引起的弯曲现象；②弯扭工况，当赛车在崎岖道路行驶时，因车轮受到地面的支承反力不对称，而使车架产生扭转现象；③制动工况，当赛车紧急制动时，由于整车质量和驾驶员自身的惯性而产生纵向力和纵向加速度；④转向工况，当赛车转向时，整车质量由于惯性离心力产生侧向力和侧向加速度而引起横向扭曲；⑤急转弯工况，当赛车在行驶过程中紧急制动进入弯道时，车辆在受纵向加速度的同时还受侧向加速度。

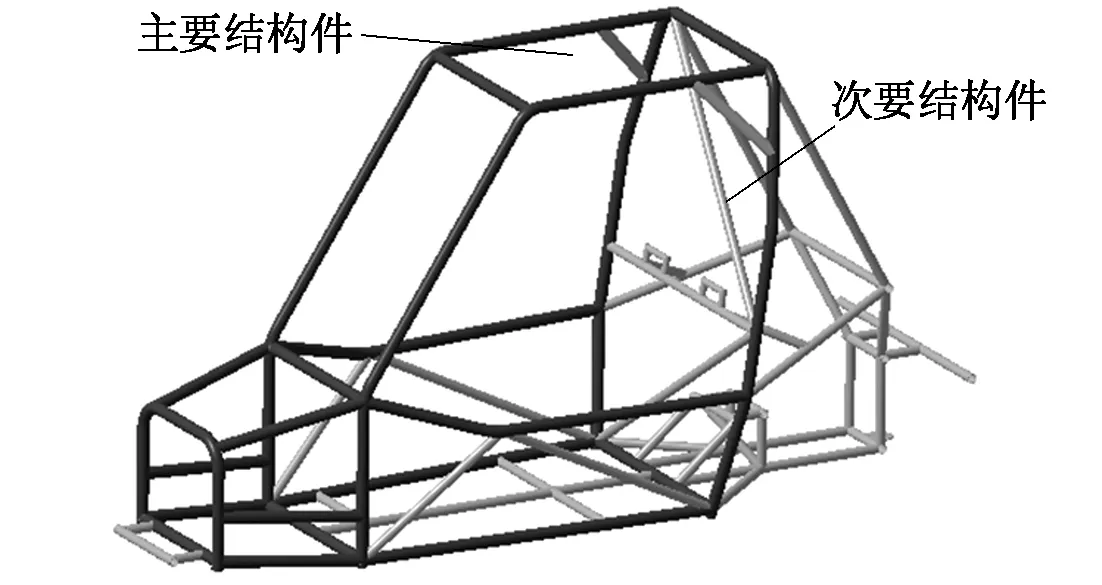
图1 车架CATIA模型

2.1 网格划分

由于车架由钢管组成，采用梁单元网格可以减少计算量。在CATIA中建立车架的线框模型，导入到ANSYS中，按照给定的尺寸建立圆管，选择线框后添加圆管，生成车架实体模型，再将所有钢管生成一个实体。添加材料划分网格，生成19 359个单元、38 708个节点。

2.2 施加载荷

由于赛车在行驶过程中还承受冲击载荷，因此车架受到的静载荷还须乘以一个动载荷系数。一般越野汽车的动载荷系数为3.5～4.0，本文动载荷系数取3.5。车架承受的静载荷及加载方式如表1所示。

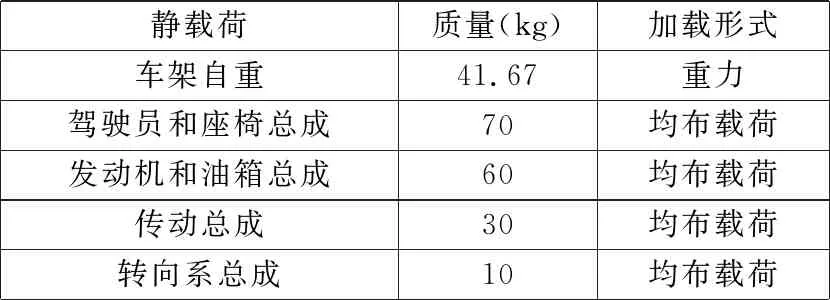
表1 车架承受的静载荷及加载方式

2.3 施加约束

对车架施加约束。将悬架与车架连接的硬点作为约束点，6个自由度分别为X、Y、Z方向的位移和旋转惯量(X为车架纵向，Y为车架横向，Z为车架质心方向)。设约束X、Y、Z方向的位移分别用1、2、3来表示，约束X、Y、Z方向的旋转惯量分别用4、5、6来表示。根据车架分析的工况不同，车架上的悬架硬点约束自由度也不同，具体约束情况如表2所示。

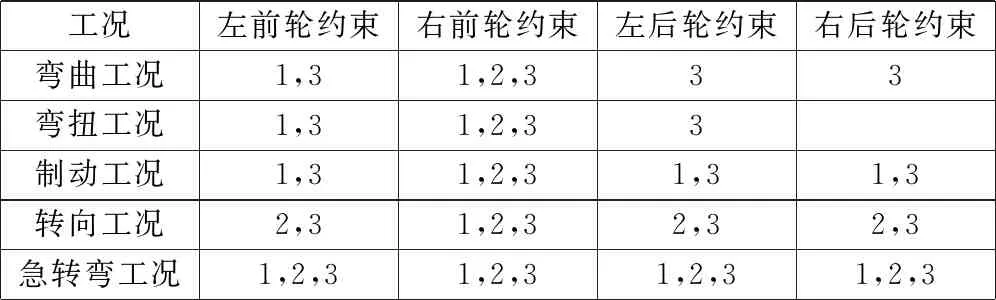
表2 强度分析中各种工况下车架的约束情况

2.4 计算结果分析

施加约束和载荷后，计算五种工况下车架的应力及形变，分析结果如表3所示。由表 3可知：最大变形产生于弯扭组合工况，最大变形值为1.457 mm，位于发动机支撑杆与主环下方杆件焊接处(如图2所示)，处在合理范围，符合设计要求；最大应力产生于弯扭工况，最大应力值为100.49 MPa，位于座椅下方杆件处(如图3所示)，远小于杆件的屈服强度785 MPa，因此后续可以对车架管件进行尺寸优化并对其力学性能加以验证，得到满足力学性能的质量更轻的车架。

表3 五种工况下车架的应力及形变分析结果

图2 弯扭工况下车架的变形云图

图3 弯扭工况下车架的应力分布

3 车架刚度分析

车架的刚度是衡量车架在受力时抵抗变形能力的指标。静载荷下抵抗变形的能力称为静刚度，包括弯曲刚度和扭转刚度。较大的静态刚度可以保证车架能够承受动态工作载荷，减小自身的振动以及提高低阶模态频率，增强车身的操纵性。若车架刚度过小，在受载时会产生较大的形变从而影响其他部件的正常工作。

3.1 弯曲刚度分析

由于BaJa赛车车架以纵向平面为中心左右对称，车架受垂直载荷时可将其简化成一根受载的梁，支点为前、后悬架的连接点。车架刚度计算示意图如图4所示。

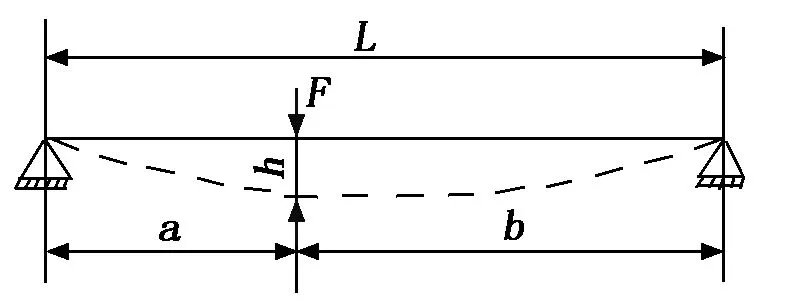
图4 车架刚度计算示意图

车架弯曲刚度SEI(Nm2)计算公式为：

(1)

其中：F为集中载荷力；h为后防滚环Z向最大变形量；a为加载点到后悬连接点的距离，a=0.424 m；b为加载点到前悬连接点的距离，b=1.196 m；L为前后悬连接点之间的纵向距离，L=1.62 m。

参照图4对车架进行约束，约束前悬架与车架连接处Z方向自由度，约束后悬架与车架连接处的X向、Y向、Z向自由度。在车架的后部防滚环顶端施加F=1 000 N 的集中力，计算后提取h值，即防滚环顶部在Z轴的最大位移，如图5所示。经计算得到弯曲刚度值为274 727.11 Nm2，一般弯曲刚度的设计参考值大于100 000 Nm2，故设计的车架弯曲刚度在合理范围内，并有一定的优化空间。

图 5 车架弯曲刚度变形云图

3.2 扭转刚度分析

由于车架的扭转角度很小，车架约束端的位移比车架的纵向尺寸和横向尺寸小得多。车架扭转刚度ST的计算公式为：

(2)

其中：M为转矩；δ为两个位移约束端Z向位移差,δ=0.02 m；S为两个位移约束端的横向距离，S=0.475 m。

对车架进行约束，对左后悬连接点施加10 mm 沿Z轴正方向的位移约束，对右后悬连接点施加10 mm 沿Z轴负方向的位移约束，对前悬架连接点施加X、Y、Z向的平移约束。车架扭转刚度变形云图如图6所示,提取计算结果，得到车架所受扭矩为10 694 N·m。由公式(2)计算扭转刚度为2 215.29 N·m/(°)，查阅资料，BaJa车架扭转刚度值一般大于1 000 N·m/(°)，故设计的车架满足要求并且存在一定的优化空间。

4 模态分析

为了避免BaJa赛车在行驶时车架与激励产生共振，需要对车架进行模态分析，将车架的固有频率与内外激励的频率进行比较，判断设计是否满足要求。

由于车架采用梁单元，因此前3阶模态固有频率为零，计算得到的前6阶非零固有频率如表4所示，1阶非零模态如图7所示。

表4 车架前6阶非零固有频率

图7 车架第1阶非零模态

赛车在行驶时，主要受道路激励和发动机激振的作用。道路激励由路面不平度来决定，查阅资料，道路激励的频率大多集中在5 Hz～20 Hz。发动机的激励频率由发动机的转速决定，比赛中所用到的发动机为百力通单缸四冲程发动机，规定的怠速为1 750 r/min左右,最高转速为3 800 r/min。通过计算，发动机在怠速时的激振频率为14.6 Hz，在最高转速时的激振频率为31.7 Hz。车架1 阶非零固有频率为39.24 Hz，车架的各阶固有频率均不与发动机以及路面激励频率接近或重合，表明设计的车架是合理的。

5 车架优化设计

5.1 车架灵敏度分析

车架灵敏度分析是分析车架性能参数对设计变量变化的敏感性，是优化设计的基础。通过灵敏度分析可获得设计变量组对设计响应的影响程度，从而确定优化方案。

由于车架是由钢管焊接而成，选取主要构件钢管内径和次要构件钢管的内径作为优化设计变量(在钢管外径不变的情况下，改变内径即改变厚度)。分析得到设计变量对车架强度、车架形变和 1 阶模态频率以及车架质量的响应灵敏度，分析结果如图 8所示。

图8 各管件厚度对响应的敏感度

从图8可以看出：次要管件内径对车架强度的影响比较大，主要管件内径对车架强度的影响稍小，表明主要管件的厚度存在一定的优化空间；主要管件厚度的增加对提高1阶模态频率有积极的影响；各管件厚度的减小对减轻车架质量有积极影响；各管件厚度对车架形变的影响几乎相等。

5.2 轻量化设计

参照灵敏度分析的结果，对设计变量的优化尺寸范围进行设定，采用响应面法对车架质量进行优化。设置车架质量目标函数最小，车架变形量目标函数最小，最大扭转应力在一定范围内最小，车架1阶固有频率默认，计算得到3组优化数据，获得车架最小质量，优化结果如表5所示。

表5 轻量化优化结果

由表5可以看出：第1组数据为最优，最大扭转应力最小为160.13 MPa，车架质量最小为38.833kg。考虑到实际情况，对优化结果进行了调整，调整后最终采用主要构件钢管内径为14.3 mm，次要构件钢管内径为11.3 mm。

5.3 车架强度和刚度优化前后对比

根据调整后的尺寸，重新建立了车架的有限元模型，对改进后的车架进行强度、刚度分析。计算结果如表6所示。

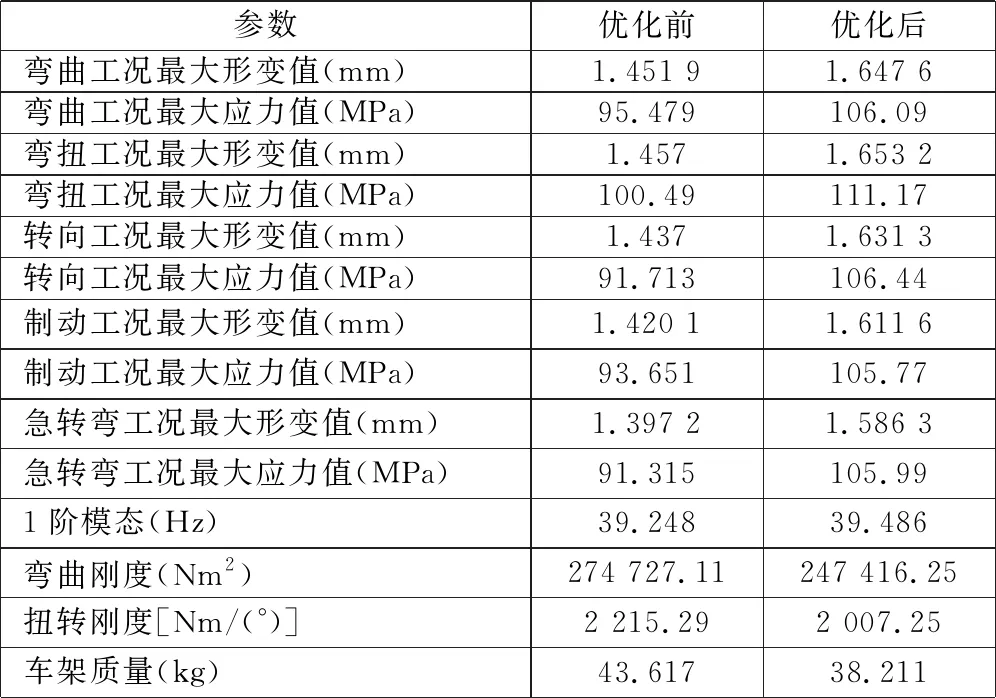
表6 优化前、后结果对比

优化后的车架在各工况下的形变和应力虽然略有增加，但还是远远小于车架钢管的屈服强度。经过优化计算，重新选定钢管的尺寸，车架的质量由原来的43.617 kg减少至 38.211 kg，质量减轻了12%，达到了赛车车架设计轻量化目标。

6 结语

本文根据巴哈大赛规则，对赛车车架进行设计，运用ANSYS对车架进行有限元分析，得到了车架在各种工况下的变形量和应力分布情况，并对车架的刚度和模态进行了分析。根据分析结果，构建了车架管件厚度对车架强度承载能力最大、车架形变最小和车架质量最小以及1阶模态频率符合性能要求的多目标优化模型，经灵敏度分析确定设计变量的优化范围，对车架钢管厚度进行了优化计算，使车架的重量减轻了12%，实现了车架轻量化设计。通过灵敏度分析来选择设计变量，采用响应面法来进行计算，使得优化效率大大增加，为车架设计提供了参考，具有一定的实际应用价值。