从属于叶形区域的一类解析函数的三阶Hankel行列式①
宋 园
(滁州职业技术学院基础部,安徽滁州239000)
0 引 言
单位圆盘U={z:|z|<1}内具有形式
f(z)=z+a2z2+a3z3+…
(1)
的解析函数的全体记为H,H中的所有的单叶函数记为S.单位圆盘U={z:|z|<1}内解析具有形式p(z)=1+c1z+c2z2+…且满足Rep(z)>0的函数的全体记为P.
令a1=1,n≥1,q≥1.Noonan和Thomas[1]引入函数f(z)的q阶Hankel行列式:
当n,q取一些特殊值时,可得
则有H3(1)=a3H2(2)-a4(a4-a2a3)+a5H2(1).
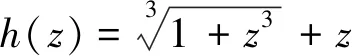
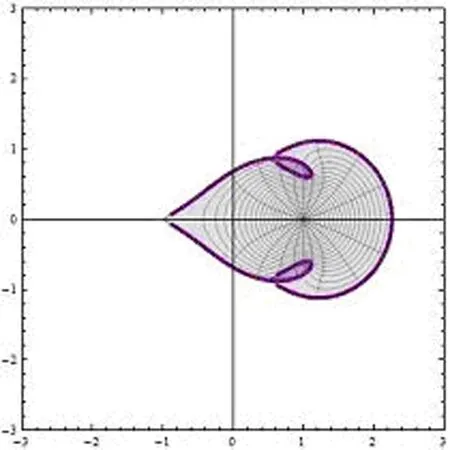
图1 叶形区域
在图1中,h(u)为一个实轴从-1到2.2、虚轴从-0.7到0.7的关于实轴对称有界的叶形区域.
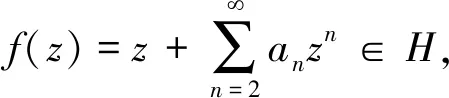
则称f(z)∈R(h).
在文献[2]中给出如下定理:
定理3.1若f(z)∈R(h),则有|a2|
|a3|
定理3.2若f(z)∈R(h),则|a2a3-a4|结果是精确的.
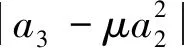
定理5.1若f(z)∈R(h),则H2(2)结果是精确的.
定理6.1若f(z)∈R(h),则H3(1)结果是精确的.
最近国内外许多作者[3-9]研究单叶函数类的三阶Hankel行列式.许多作者在研究前几项系数时用引理1导致结果有误差,在处理二阶Hankel行列式时出现处理错误导致结果错误.本文用引理1、2得到了函数类f(z)∈R(h)的三阶Hankel行列式,改进了文献[2]的结果.
引理1[10]假设p(z)=1+c1z+c2z2+…∈P,则
|pn|2 (n≥1).
引理2[11]假设p(z)=1+c1z+c2z2+…∈P,则存在复数y、z(|y|1,|z|1,)满足
1 主要结果
定理1若f(z)∈R(h),则有|a2|结果是精确的.
证明:如果f(z)∈R(h),那么存在施瓦兹函数ω(z)(ω(0)=0,|ω′(0)|<1),使得
(3.1)
令
则
(3.2)
将(3.2)式带入(3.1)式的右边得
(3.3)
简单计算得
f′(z)=1+2a2z+3a3z2+4a4z3+5a5z4+…
(3.4)
由(3.1), (3.2)和(3.3)式得
(3.5)
(3.6)
(3.7)
(3.8)
由(3.5)式及引理1得|a2|等号成立仅需c1=2.
由(3.6)式和引理2得
令|y|=t∈[0,1],|c1|=c∈[0,2],则有
|a3|
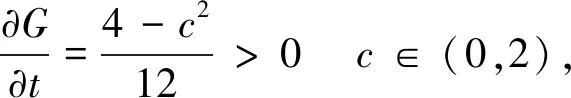
|a3|
由引理2知上式等号成立只需c=c1=0,t=1,c2=2.
由(3.7)式和引理2得
令|y|=t∈[0,1],|c1|=c∈[0,2],则有
|a4|
3t2(4-c2)(c-2)]=G(c,t).
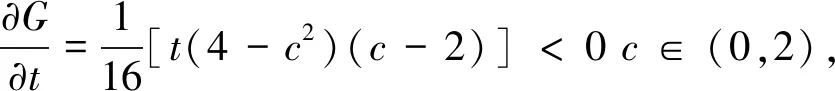
由(3.8)式及引理1得|a5|等号成立仅需c1=2.
注释1:|a4|的估计要比文献[2]中定理3.1的估计精确.
定理2若f(z)∈R(h),|a2a3-a4|结果是精确的.
证明:由(3.5),(3.6)和(3.7)式可得
(3.9)
令|y|=t∈[0,1],|c1|=c∈[0,2],由(3.9)和引理2及三角不等式得
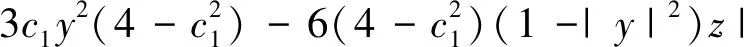
3t2(4-c2)(c-2)]=G(c,t).
下面讨论二元函数G(c,t)在[0,2]×[0,1]内最大值.考虑
在[0,2]×[0,1]只得到可能的极值点(0,0).
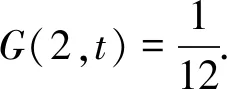
所以
|a2a3-a4|
由引理2得等号成立只需t=0,c=c1=c2=0,c3=2.
注释2:定理2中的估计比文献[2]定理3.2的估计精确.
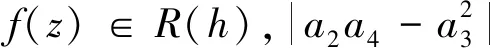
证明:由(3.5),(3.6)和(3.7)式可得
由引理2得
(3.10)
令|y|=t∈[0,1],|c1|=c∈[0,2],由(3.10)和引理2及三角不等式得
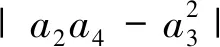
t2(4-c2)(c2-18c+32)]=G(c,t).
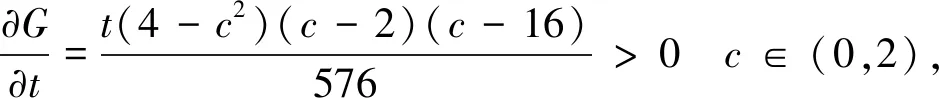
G(c,t)
由引理2知道等号成立只需c=c1=c3=0,y=t=1,c2=2.
注释:文献[2]在处理时出现错误.
定理4若f(z)∈R(h),则H3(1)
证明:由定理1,定理2,定理3及定理4.1可得定理4.

