基于货物列车抗脱轨安全度的重载铁路轨道结构强化措施评价

龚凯，向俊，刘林芽

(1.华东交通大学铁路环境振动与噪声教育部工程研究中心，江西南昌，330013；2.中南大学土木工程学院，湖南长沙，410075)

随着重载铁路货物列车行车速度提高、编组车辆数增多、行车密度增大，既有轨道结构强度、刚度、稳定性等储备下降，行车安全受到影响。为保证重载铁路货物列车安全、平稳运行，国内外学者针对重载铁路轨道结构强化技术开展了理论和试验研究，如翟婉明等[1-2]研究了道岔、路基及山区小半径曲线轨道强化措施对轮轨力、车体加速度及钢轨位移等动力学指标的影响；王斌[3]分析了山区铁路小半径曲线轨道结构参数对轮轨力、钢轨加速度等指标的影响，为提出更换重型钢轨、轨枕等强化措施提供理论基础；田宝红等[4-5]针对大秦线上出现的轨道结构病害，对安装了轨撑、加强型弹条等强化设备后的轨道结构进行了试验和现场测试，采用脱轨系数、轮重减载率等指标评价了轨道结构强化效果；杨德修[6]分析了轴重、速度及运量对重载铁路轨道结构的影响，提出了采用60 kg/m以上重型耐磨钢轨、更换III型轨枕及配套扣件、换填I 级道碴等强化措施；王建强等[7]调查了京包铁路上轨道结构病害情况，提出采用75 kg/m 钢轨替换60 kg/m 钢轨，直线路段应采用III轨枕等强化对策；王福[8]根据现场调研和动态测试结果研究了大包铁路客货混运重载运输条件下钢轨适应性，提出了提高钢轨等级、强化小半径曲线等措施；薛继连[9]研究了30 t 轴重下朔黄铁路轨道结构适应性，重点研究了SH-I 型重型轨枕及重型扣件等强化效果。然而，上述研究多采用轮轨力、轨道各部件动力响应等动力学指标、脱轨系数和轮重减载率对轨道强化措施进行评价，未能反映轨道强化措施对货物列车抗脱轨安全度的影响，关于轨道结构强化后货物列车抗脱轨信息尚不明确，轨道结构强化后列车抗脱轨能力提升幅度缺乏定量的认识。因此，根据重载铁路货物列车-轨道系统(FTT 系统)横向振动稳定性分析方法[10]，本文作者提出基于货物列车抗脱轨安全度(列车抗脱轨安全度是指列车的抗脱轨能力临界车速和容许极限车速)的重载铁路轨道结构强化措施评价方法；以提高钢轨等级、采用III 型轨枕、强化扣件及道床等轨道结构强化措施为例，采用上述评价方法，分析并量化轨道结构强化措施对货物列车抗脱轨能力、临界车速、容许极限车速及列车运行平稳性的影响，为我国评价及制定具有预防货物列车脱轨功能的轨道强结构化措施提供参考。

1 FTT 系统横向振动稳定性分析方法

研究表明[11]，列车脱轨机理是列车车轮轮缘逐渐爬上钢轨顶部中点的过程，是FTT 系统由小幅横向振动发展为大幅横向振动直至横向振动失稳的过程。要研究货物列车抗脱轨安全度，必须分析FTT 系统横向振动稳定性。FTT 系统具有时变性，它是货物列车与轨道结构耦合运动随时间变化的过程。将货物列车的机车、车辆离散为考虑车体、前后转向架纵向、横摆、浮沉、侧滚、点头、摇头运动及轮对横摆、浮沉运动的26 个自由度的多刚体系统，进而可得货物列车空间振动总势能ΠV[12]。同时，计算长度为L轨道结构可离散为n个轨段单元，每个轨段单元考虑为具有34个自由度的有限元模型(如图1 所示)，视钢轨为弹性点支承Euler 梁、轨枕为弹性变形体，不计轴向变形及扭转变形；扣件模拟为线性弹簧及黏滞阻尼器；假定轨枕置于弹性道床上，不考虑道床本身振动，则道床顶面模拟线性弹簧及黏滞阻尼器，模型中，扣件竖向和横向弹性系数分别为K1和K2，扣件竖向和横向阻尼系数分别为C1和C2，道床竖向和横向弹性系数分别为K4和K5，道床竖向和横向阻尼系数分别为C4和C5，轨枕与道床间的纵向弹性系数和阻尼系数分别为K3和C3。可导出轨道空间振动总势能ΠT[12]。通过叠加可导出货物列车-轨道系统空间振动总势能为

图1 轨道空间振动分析模型Fig.1 Spatial vibration analysis model of track

设t时刻，在计算长度为L的轨道上运行着m辆货车，按照弹性系统动力学总势能不变原理[13]及形成系统矩阵的“对号入座”法则[14]，得出FTT系统在t时刻的矩阵方程为

式中：K，C，M和P分别为FTT 系统空间振动的刚度矩阵、阻尼矩阵和质量矩阵及荷载列阵；{δ}，分别为相应的位移列阵、速度列阵和加速度列阵；采用构架人工蛇行波和轨道竖向几何不平顺分别作为FTT 系统横向和竖向振动激振源，并按照Wilson-θ逐步积分法求解式(2)。求解时，因车轮与钢轨接触位置不同，使得每计算一时间步长FTT系统矩阵都会发生变化，具有时变性。

针对FTT 系统的时变性，现有运动稳定性分析理论(如相平面法、李雅普诺夫函数法等)均不能直接用于分析FTT系统横向振动的稳定性[11]。但由物理概念和理论分析表明，系统状态的稳定性可由系统能否经得起干扰来判别，经得起干扰的系统平衡状态是稳定的，因为干扰引起的系统抗力增量大于荷载增量，使干扰引起的位移消失，系统恢复至原来的平衡状态；反之，则是不稳定的，因为干扰引起的系统抗力增量小于荷载增量，使干扰位移和扰动振动不断增长，使系统状态消亡。因此，系统平衡状态稳定性的力素增量判别准则为当抗力增量大于荷载增量时，系统稳定；当抗力增量小于荷载增量时，系统不稳定；抗力增量等于荷载增量时，系统平衡状态处于失稳临界状态。

FTT系统因横向振动方程的数目很多且随列车运动变化，难以建立其平衡状态稳定性的力素增量判别准则，只能从力的作用与力做功的作用等价的角度将力素增量判别准则转化为抗力做功增量与输入能量增量的判别准则，即抗力做功增量大于输入能量增量时，系统稳定；抗力做功增量小于输入能量增量时，系统不稳定；抗力做功增量等于输入能量增量时，系统处于临界失稳状态。由此，建立FTT 系统横向振动判别准则：当Δσc>Δσp时，FTT 系统横向振动稳定；当Δσc<Δσp时，FTT 系统横向振动不稳定；当Δσc=Δσp时，FTT 系统横向振动处于失稳临界状态。其中，Δσpr和Δσcr分别为FTT 系统横向振动输入能量增量及抗力做功增量。前者已通过现场实测货物列车构架蛇行波，统计了蛇行波标准差σp与车速v的关系曲线[11]，由此可确定FTT系统横向振动输入能量随车速变化的增量Δσpr(即车速v0～vr时输入能量σp0与σpr之差)；而后者则需采用试算法计算货物列车脱轨全过程[11]，建立FTT系统横向振动极限抗力做功σc与车速v的关系曲线(σc-v曲线)，σc为列车脱轨时FTT系统的最大抗力做功，反映了FTT系统抗脱轨的能力，进而根据σc-v曲线计算FTT 系统横向振动极限抗力做功随车速v变化的增量Δσcr(即车速v0～vr时抗力做功σc0与σcr之差)。

将Δσcr=Δσpr时对应的车速称为FTT系统横向振动失稳临界车速vcr(简称临界车速)，并将vcr/K作为FTT 系统横向振动容许极限车速vL(安全系数K取为1.25[15]），并以容许极限车速vL为上限，采用国际通用的Sperling平稳性指标分析货物列车运行平稳性。

2 基于货物列车抗脱轨安全度的重载铁路轨道结构强化措施评价方法

根据上述重载铁路FTT 系统横向振动稳定性分析方法，提出基于货物列车抗脱轨安全度的重载铁路轨道结构强化措施评价方法如下。

1)将轨道结构强化措施引入FTT 系统空间振动矩阵方程中，建立考虑轨道结构强化措施的FTT系统空间振动矩阵方程。将75 kg/m轨的截面特性及材料属性输入矩阵方程来模拟提高钢轨等级这一强化措施。

2)计算考虑轨道结构强化措施的FTT 系统横向振动输入能量增量Δσpr。当车速为90 km/h 及以下时，FTT 系统横向振动输入能量σp见文献[11]；当车速大于90 km/h 时，σp由文献[16]所述方法得到，并形成σp-v曲线，如图2所示。

考虑到尚缺少轨道部件强化后FTT 系统横向振动输入能量的相关资料，且列车脱轨试验较难轻易实现，在判别轨道部件强化前后FTT 系统横向振动稳定性时，σp均按照图2 中的σp-v曲线取值。实际上，按照图2中的σp-v曲线取值并判断轨道结构部件强化后FTT 系统横向稳定性对实际轨道结构部件强化效果有利。因为轨道结构部件强化会提高轨道结构横向刚度，而相应的实际输入能量小于轨道结构强化前FTT 系统输入能量，若仍采用轨道结构强化前输入能量作为轨道结构部件强化后的输入能量，则实际轨道结构强化后货物列车具有更大的安全裕量。

图2 FTT系统σp-v曲线Fig.2 σp-v curves of FTT system

3)计算考虑轨道结构强化措施的FTT 系统横向振动抗力做功增量Δσcr.。采用试算法计算考虑轨道结构强化措施的货物列车脱轨全过程，得到相应的抗力做功σc与车速v的曲线关系，分析轨道结构强化措施对货物列车抗脱轨能力的影响，进一步计算Δσcr。

4)计算Δσcr=Δσpr时考虑轨道结构强化措施的FTT系统横向振动失稳临界车速vcr和容许极限车速vL。分析轨道结构强化措施对vcr和vL的影响，并以容许极限车速vL为上限，采用国际通用的Sperling平稳性指标分析货物列车运行平稳性。

3 实例分析

计算1 辆机车+10 辆空载敞车在轨道上运行时的FTT 系统横向振动稳定性。轨道计算长度为200 m，直线轨道，钢轨等级为60 kg/m，轨枕为II型混凝土轨枕。扣件横向刚度和道床横向刚度分别为30 MN/m 和3.808 MN/m[17]，研究提高钢轨等级、采用III 型轨枕、强化扣件及道床等轨道强化措施对货物列车抗脱轨安全度的影响。

3.1 提高钢轨等级对货物列车抗脱轨安全度的影响

将60 kg/m 钢轨更换为75 kg/m 钢轨，75 kg/m钢轨的截面尺寸及材料特性见文献[18]。按照前述分析方法，分别计算不同车速下，60 kg/m 钢轨和75 kg/m 钢轨时FTT 系统横向振动极限抗力做功，σc-v曲线如图3所示。鉴于货物列车脱轨大多在50 km/h以上，故以50 km/h作为检算起点[11]，且考虑到计算和测试误差，车速每增加10 km/h 检算1 次FTT系统横向振动稳定性，计算结果见表1和表2。

由图3可知：60 kg/m钢轨和75 kg/m钢轨条件下，FTT 系统横向振动极限抗力做功σc均随车速v增大，σc最大值分别为317 cm/s2和376 cm/s2，可见，提高钢轨等级后FTT 系统抗脱轨能力较轨道结构强化前提高了18.6%。

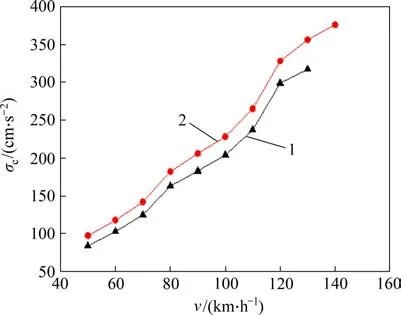
图3 60 kg/m和75 kg/m钢轨条件下σc-v曲线Fig.3 σc-v curves for 60 kg/m rail and 75 kg/m rail

由表1可知：在120～130 km/h和130～140 km/h之间必定存在临界车速使Δσcr=Δσpr。按照内插法，采用60 kg/m 钢轨和75 kg/m 钢轨时，FTT 系统横向振动失稳临界车速vcr分别为122.72 km/h和134.0 km/h，考虑安全系数为1.25，得到相应的容许极限车速vL分别为98.18 km/h 和107.2 km/h。可见：与60 kg/m钢轨相比，75 kg/m钢轨的容许极限车速可提高9.2%。

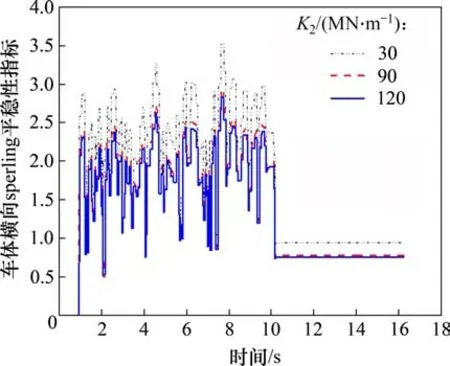
为分析提高钢轨等级对货物列车运行平稳性的影响，计算v=80 km/h(即v＜vL)时FTT 系统振动响应。提高钢轨等级前后车体横向Sperling平稳性指标时程曲线如图4所示。

由图4可知，60 kg/m钢轨和75 kg/m钢轨的第2 车车体横向Sperling 平稳性指标最大值分别为3.52和3.29。可见：与60 kg/m钢轨相比，75 kg/m钢轨的第2 车车体横向Sperling 平稳性指标减小6.5%。说明提高钢轨等级对改善列车运行平稳性影响较小。

图4 60 kg/m和75 kg/m钢轨第2车车体横向Sperling平稳性指标时程曲线Fig.4 Lateral Sperling stability index of the second vehicle body for 60 kg/m rail and 75 kg/m rail

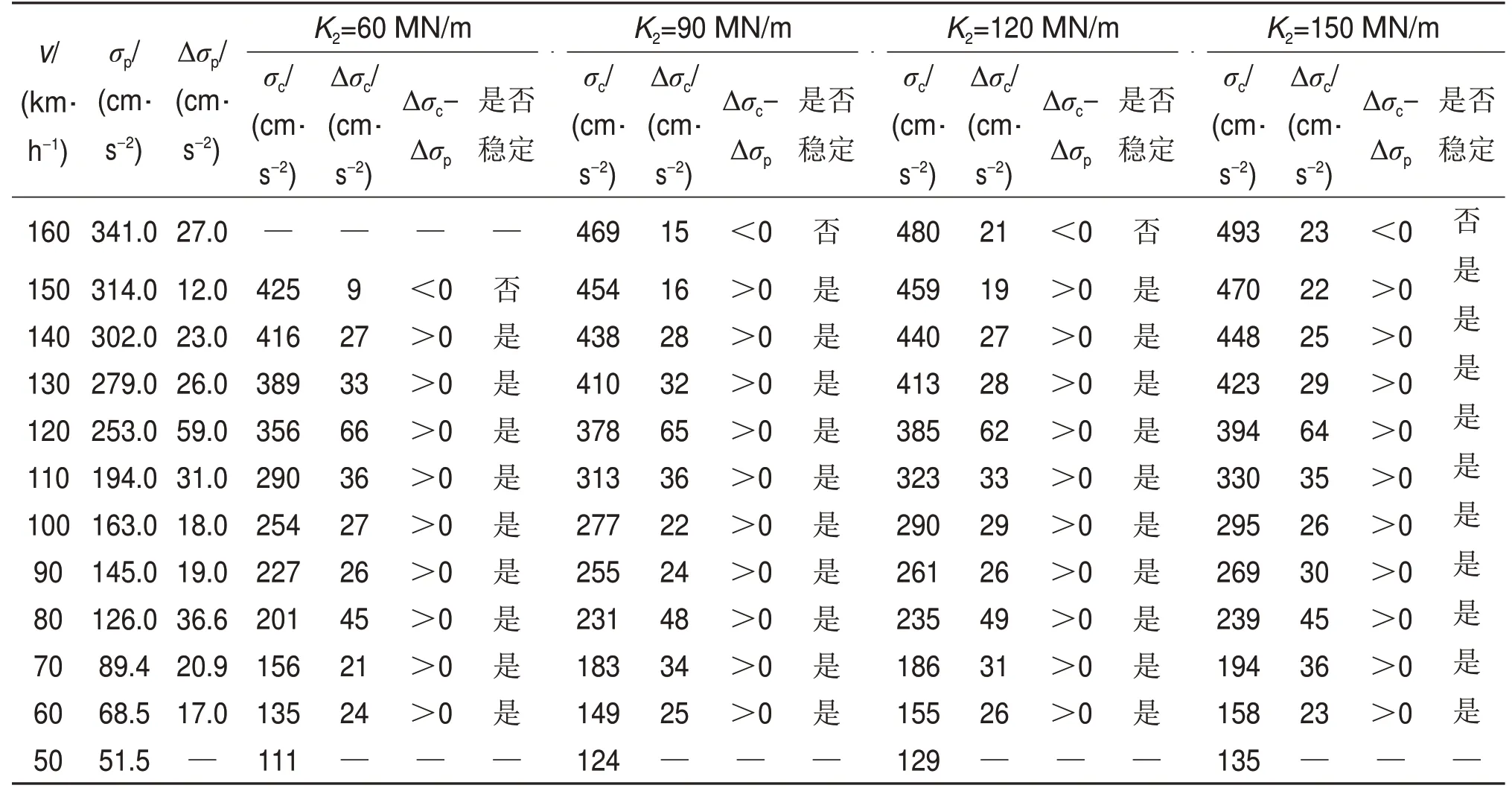
表1 提高钢轨等级下FTT系统横向振动稳定性计算结果Table 1 Calculation results of lateral vibration stability of FTT system under improved rail grade

3.2 采用III 型轨枕对货物列车抗脱轨安全度的影响

将II 型轨枕更换为III 型轨枕用于模拟轨道部件强化措施，III 型轨枕的截面尺寸及材料特性见文献[18]。按照前述分析方法，计算不同车速下II型、III 型轨枕时FTT 系统横向振动极限抗力做功σc，σc-v曲线如图5所示。III型轨枕时FTT系统横向振动稳定性计算结果见表2。由图5 可知：II 型轨枕和III 型轨枕条件下FTT 系统横向振动极限抗力做功σc均随车速逐渐增大，σc最大值分别为317 cm/s2和406 cm/s2。可见，采用III 型轨枕替换II 型轨枕FTT系统抗脱轨能力提高了28.1%。

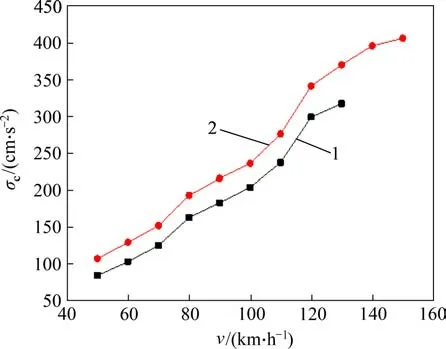
图5 II型和III型轨枕时σc-v曲线Fig.5 σc-v curves for II type sleeper and III type sleeper

由表2可知：在140～150 km/h之间必定存在临界车速使得Δσcr=Δσpr。按照内插法，可得FTT系统横向振动失稳临界车速vcr为145.99 km/h，考虑安全系数1.25，则相应的容许极限vL=116.79 km/h。可见，采用III 型轨枕替换II 型轨枕FTT 系统横向振动容许极限车速可提高18.9%。

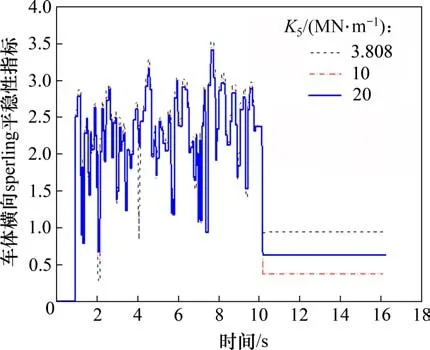
为分析采用III 型轨枕对货物列车运行平稳性的影响，计算v=80 km/h(即v

3.3 扣件强化对货物列车抗脱轨安全度的影响

通过增大轨道扣件横向刚度K2来模拟扣件强化措施。按照前述分析方法，假定扣件横向刚度K2分别为60，90，120 和150 MN/m，扣件强化前的横向刚度为30 MN/m。计算不同车速v和扣件横向刚度K2下FTT 系统横向振动极限抗力做功σc，相应的σc-v曲线如图7 所示。由图7 可知：随着v和K2增 大，σc增大，当K2为60，90，120 和150 MN/m 时，σc最大值分别为425，469，480 和493 cm/s2，σc较K2为30 MN/m 时分别提高了34.1%，47.9%，51.4%，55.5%。可见，K2增大后，FTT 系统抗脱轨能力大幅度提升，但当K2小于90 MN/m时，FTT 系统抗脱轨能力提高比例较大，而当K2大于90 MN/m 时，FTT 系统抗脱轨能力增长幅度变缓。

表2 III型轨枕条件下FTT系统横向振动稳定性计算结果Table 2 Calculation results of lateral vibration stability of FTT system under III type sleeper

图6 不同类型轨枕条件下第2车车体横向Sperling平稳性指标时程曲线Fig.6 Lateral Sperling stability index of the second vehicle body for different type sleeper

图7 不同扣件横向刚度K2的σc-v曲线Fig.7 σc-v Curves for different K2

扣件强化条件下FTT 系统横向振动稳定性计算结果见表3 所示。由表3 可知：K2分别为60，90，120 和150 MN/m 时，在140～150 km/h 和150～160 km/h之间必定存在某车速使得Δσcr=Δσpr。按照内插法，得出K2分别为60，90，120 和150 MN/m时FTT 系统横向振动失稳临界车速vcr分别为145.72，152.5，155.38 和157.14 km/h，考虑安全系数1.25，可得相应的容许极限车速分别为116.58，122.00，124.30 和125.71 km/h。可见，较扣件横向刚度增大前FTT 系统横向振动容许极限车速分别提高了18.7%，24.3%，26.6%和28.0%。当K2＞120 MN/m时提升幅度较小。

为分析扣件强化对货物列车运行平稳性的影响，计算v=80 km/h(即v

3.4 道床强化对货物列车抗脱轨安全度的影响

通过增大道床横向刚度K5来模拟扣件道床强化措施。按照前述分析方法，假定道床横向刚度K5分别为5，10，15和20 MN/m，道床强化前的横向刚度为3.808 MN/m。计算不同车速v和不同道床横向刚度K5下FTT 系统横向振动极限抗力做功σc，相应的σc-v曲线如图9 所示。由图9 可知：随着v和K5增大，σc增大，K5分别为5，10，15 和20MN/m时σc最大值分别为420，479，498和506 cm/s2，较K5为3.808 MN/m 时分别提高了32.5%，51.1%，57.1%和59.6%，且当K5＜15 MN/m 时，FTT 系统抗脱轨能力随K5提高较大，当K5＞15 MN/m 时，FTT系统抗脱轨能力增大幅度较小。

表3 扣件强化条件下FTT系统横向振动稳定性计算结果Table 3 Calculation results of lateral vibration stability of FTT system under fastener strengthening

图8 不同K2时第2车车体横向Sperling平稳性指标时程曲线Fig.8 Lateral Sperling stability index of the second vehicle body for different K2

图9 不同道床横向刚度K5时的σc-v曲线Fig.9 σc-v Curves for different K5

由表4 可知：K5分别为5，10，15 及20 MN/m时，在140～150 km/h 和150～160 km/h 之间必定存在临界车速使得Δσcr=Δσpr。按照内插法，可得K5分别为5，10，15 和20 MN/m 时FTT 系统横向振动失稳临界车速分别为146.67，153.90，155.83 及158.18 km/h，相应的容许极限车速分别为117.34，123.20，124.67和126.56 km/h，其较道床强化前提高19.5%，25.5%，27.0%和28.9%。

分析道床强化对货物列车运行平稳性的影响，计算v=80 km/h(即v＜vL)时FTT 系统振动响应。不同K5条件下第2 车车体横向Sperling平稳性指标时程曲线如图10所示。由图10可知：K5分别为10和20 MN/m 时第2 车车体横向Sperling 平稳性指标最大值分别为3.46 和3.41，较K5为3.808 MN/m 时分别减小1.7%和3.1%。可见，强化道床对车体横向Sperling平稳性指标影响较小。

表4 道床强化条件下FTT系统横向振动稳定性计算结果Table 4 Calculation results of lateral vibration stability of FTT system under ballast bed strengthening

图10 不同K5时第2车车体横向Sperling平稳性指标时程曲线Fig.10 Lateral Sperling stability index of the second vehicle body for different K5

4 结论

1)提高钢轨等级时FTT 系统抗脱轨能力提高了18.6%，相应的临界车速及容许极限车速分别为134.0 和107.2 km/h，而采用III 型轨枕时FTT 系统抗脱轨能力提高了28.1%，相应的临界车速及容许极限车速分别为145.99 和116.79 km/h。可见，与提高钢轨等级相比，采用III 型轨枕对提高货物列车抗脱轨安全度作用更加显著。

2)强化扣件后抗脱轨能力最大可提升55.5%，相应的临界车速及容许极限车速分别为157.14 km/h和125.71 km/h；强化道床后抗脱轨能力最大可提升59.6%，相应的临界车速及容许极限车速分别为158.18 km/h 和126.56 km/h，但当强化后的扣件横向刚度达到120 MN/m 时，货物列车抗脱轨能力、临界车速、容许极限车速增幅较小，且当横向刚度大于15 MN/m 后，强化后的道床也出现类似现象。可见，强化扣件或道床可大幅提升货物列车抗脱轨安全度，但应分析其提升幅度的变化，制定合理且经济的强化措施。

3)4种轨道强化措施对货物列车运行平稳性均具有一定的改善，但强化道床效果较小。