带窗洞自保温暗骨架承重墙抗震试验及承载力计算

刘康，岳艺博，王少杰，刘福胜，周满，孙宏伟

(1.山东农业大学水利土木工程学院，山东泰安，271018；2.中南大学土木工程学院，湖南长沙，410083)

为了满足自然通风、采光等，墙体开设窗洞十分普遍，窗洞正下方对应墙体通常称为窗下墙、其两侧墙体通常称为窗间墙。已有研究及历次震害调查均表明[1-4]：窗间墙宽度显著影响砌体结构抗震性能，GB 50011—2010“建筑抗震设计规范”[5]针对传统砌体结构窗间墙的宽度提出了明确限值。近年来，窗下墙对砌体结构抗震性能的影响已引起广泛关注，信任等[6]通过设计制作缩尺比为1/3的三层三跨烧结黏土砖砌体结构，通过拟静力低周往复加载试验研究了窗下墙对抗震性能的影响。目前，对考虑窗下墙抗震性能的新型砌体结构的研究较少。自保温暗骨架承重墙集抗震节能于一体，属于约束砌体结构，HOU 等[7-9]对该新型结构进行了研究。在此，本文作者设计制作带窗洞的自保温暗骨架承重墙足尺试件，采用低周往复荷载试验研究该新型墙体结构的抗震性能；并以试验为基础，通过理论分析修正建立墙体的开裂荷载、极限荷载计算与分配方法，最终定量评价窗下墙、窗间墙参与墙体抗震的作用机制。

1 试验概况

1.1 试件设计与制作

抗震试验试件设计与制作示意图如图1 所示。制作2 片带窗洞足尺自保温暗骨架承重墙试件W1和W2，墙体宽×高×厚为2.79 m×2.50 m×0.24 m，由全角型、半角型及水平条带3种节能承重砌块砌筑而成，砌筑用砂浆和块材强度等级分别为Mb7.5和MU10；在墙体两端及窗洞两侧共设置4根竖向芯柱，在第4、第8 皮砌块内浇筑钢筋混凝土水平条带，各芯柱、水平条带均内置1 根14 mm 的HRB335 级钢筋，所采用的混凝土强度等级均为Cb30。试件W1 和W2 对应的窗洞宽分别为0.81 m和1.21 m，洞口高均为1.40 m；两侧窗间墙宽分别为0.99 m和0.79 m，窗下墙高均为0.80 m。墙体试件制作完成后养护28 d 实施加载，在其根部设有现浇钢筋混凝土底梁。

1.2 加载制度与数据采集

1.2.1 加载制度

根据JGJ/T 101—2015“建筑抗震试验规程”[10]对试件W1 和W2 进行低周往复荷载试验，加载采用荷载变形双控制方案，具体加载制度如下：

1)根据典型四层村镇住宅底层墙体实际承担的竖向压力统计，扣除墙体顶梁及其上部钢垫梁自重后，通过2个作动器同步施加竖向荷载，每个竖向作动器施加压力为55 kN，对应轴压比为0.04。竖向荷载通过钢垫梁、顶梁均匀分配至墙体，可在试验全过程模拟竖向荷载恒定作用。

2)低周往复水平荷载通过反力墙、水平作动器施加，正式加载前先进行预加载。正式试验分为力控制和位移控制2个阶段。墙体开裂前，以力控制加载，第1 级荷载取20 kN，随后采用逐级加荷方法，每级荷载循环1次，试件接近开裂荷载时减小荷载步长；墙体开裂后，改为位移控制加载，每级荷载循环3次，当荷载下降至极限荷载的85%时停止加载，结束试验。

1.2.2 数据采集

加载期间采集力、变形、应变、裂缝发展情况等，其中，加载力与对应变形由MTS 系统自动采集并存储记录，墙体砌块表面与钢筋的应变通过应变仪采集，裂缝发展情况由试验人员通过裂缝测宽仪观测并记录其演化分布规律，侧向变形则通过电测位移计采集，对应测点布置方案见图1(a)和1(c)。

图1 试件设计与制作示意图Fig.1 Schematic diagram of design and construct of specimens

2 试验现象

2.1 力控制阶段

在力控制加载初期墙体无明显开裂现象，随着力增加，墙体出现开裂，试件W1 和W2 的开裂荷载分别为140.655 kN和100.573 kN，对应侧向变形分别为4.211 mm 和2.399 mm，因此，将±4 mm和±2 mm 分别作为试件W1 和W2 后续位移控制加载阶段的第1 荷载步。如图2(a)所示，试件W1 首条裂缝为水平裂缝，位于窗下墙第4 皮砌块下部；随后在该条水平裂缝的中部向左下2皮砌块发展出现新的阶梯状裂缝。如图3(a)所示，与试件W1 相同，试件W2 的首条裂缝亦出现在第4 皮砌块下部，但裂缝长度较试件W1 显著变短；随后在第3皮砌块下部出现1条长约35 cm的水平裂缝。

2.2 位移控制阶段

试件W1在位移控制加载各阶段的破坏特征如图2(b)～(f)所示。当水平位移加载至±4 mm时，窗下墙第3和第4皮砌块之间的水平裂缝贯通并在窗下墙左侧出现新的水平裂缝，窗角左侧开始出现阶梯状裂缝；侧移增至±8 mm 时，率先在窗洞正下方窗下墙区域形成交叉的阶梯状“X”型裂缝，且在该区域的左右两侧第2和第3皮砌块之间有出现水平、竖向裂缝并形成阶梯状裂缝的趋势；侧移增至±12 mm 时，窗下墙裂缝已得到较充分发展，多条平行的阶梯状裂缝已形成，在左右两侧窗间墙的第9～11皮砌块之间亦出现了阶梯状裂缝，同时在两侧窗间墙有水平裂缝出现；侧移增至±14 mm时，除已经存在的裂缝继续发展外，新的阶梯状裂缝主要出现在左右两侧窗间墙的第5～7皮砌块之间，至此裂缝基本在墙体各区域满布；侧移增至±16 mm时，窗间墙与两侧窗下墙形成的各阶梯型裂缝得到进一步发展，墙体表面有少许剥落现象，对应荷载已降至极限荷载的85%以下，结束加载。

试件W2在位移控制加载各阶段的破坏特征如图3(b)～(f)所示。当水平位移加载至±4 mm时，在窗下墙第3皮砌块上下灰缝处出现了水平裂缝，并与前期裂缝相连初步形成阶梯状裂缝；侧移增至±10 mm时，窗下墙裂缝分别向左下、右下方向发展，并在第2～4 皮砌块间形成2 条阶梯状裂缝；侧移增至±16 mm 时，窗下墙第3 和第4 皮砌块间水平灰缝裂缝贯通并在其下侧区域形成新的阶梯状裂缝，两侧窗间墙开始出现开裂现象；侧移增至±20 mm时，窗下墙裂缝基本处于稳定状态，新的裂缝主要出现在两侧窗间墙，且两侧窗间墙裂缝发展受暗骨架的阻隔明显；侧移增至±24 mm时，窗下墙、窗间墙对应裂缝发展均已较为充分，卸载后裂缝已不能完全闭合，墙体表面和两侧翼缘处有明显剥落现象，对应荷载降至极限荷载85%以下，结束加载。

图2 试件W1失效破坏过程Fig.2 Failure process of sample W1

图3 试件W2失效破坏过程Fig.3 Failure process of sample W2

综上可知，试件W1 和W2 破坏特征相似，破坏顺序均是起于窗下墙而后发展至窗间墙，最终都是在暗骨架所包围的区格内形成阶梯状斜裂缝；因洞口宽度不同，两者在刚度退化、滞回耗能、延性系数等方面存在差异。

3 试验结果与分析

3.1 滞回曲线

图4所示为试件W1和W2的滞回曲线。由图4可知：2个试件的共同特性是：1)墙体开裂前，水平位移很小，滞回曲线基本均为直线，加卸载曲线基本重合，卸载后残余变形很小，即墙体处于弹性阶段；2)墙体开裂至极限荷载阶段，滞回曲线开始向位移轴倾斜，刚度逐渐降低，抗侧承载力继续提高，卸载后有一定的残余变形，滞回环面积不断增大，此阶段墙体处于弹塑性阶段；3)极限荷载后，抗侧承载力退化，滞回曲线进一步向位移轴倾斜，滞回环更加饱满，面积明显增大，卸载后墙体残余变形更大，刚度退化明显，最终失效破坏。试件W1 和W2 的不同之处是：试件W1的滞回曲线趋近于梭形，形状更为饱满，耗能能力更强，试件后期具有良好的塑性变形能力；试件W2的滞回曲线趋近于弓形，饱满程度比试件W1的低，即抗震耗能能力较低，但开裂荷载后对应的弹塑性变形阶段更长，相同侧移对应的抗侧承载力比试件W1的低。

3.2 骨架曲线

图5 所示为试件W1 和W2 的骨架曲线。试件W1 和W2 的共同特性是：加载初期，骨架曲线基本均呈直线；墙体开裂时，骨架曲线出现拐点，斜率变小、刚度降低，持续至极限荷载；极限承载力之后，骨架曲线呈下降趋势，至试验结束。试件W1和W2的不同之处是：1)在加载全过程试件W1的骨架曲线基本均外包试件W2的骨架曲线，说明在相同侧向变形下，试件W1的抗侧承载力更高，即伴随窗间墙变窄墙体抗侧承载力下降，显然，试件W1极限承载力也比试件W2的高；2)在骨架曲线峰值区域，试件W1的侧向变形能力比试件W2 的低，即达到极限荷载后，试件W1 骨架曲线下降相对较快，试件W2 骨架曲线下降相对缓慢，说明试件W2具有更好的变形能力。

图4 试件滞回曲线Fig.4 Hysteretic curves of specimens

图5 试件骨架曲线Fig.5 Skeleton curves of specimens

3.3 荷载特征值和延性

开裂、屈服、极限荷载、极限变形等是墙体受力的特征点，对应的荷载及变形见表1。由表1可知：试件W1的开裂、屈服、极限及破坏荷载较试件W2均显著提高，如开裂荷载和极限荷载分别提高了39.85%和12.98%，这是窗间墙变窄所致，即窗间墙宽度降低对墙体抗侧承载力存在显著的削弱作用。

延性是构件或试件在破坏以前所能承受的后期变形能力，通常采用延性系数[11]表征，即极限位移与屈服位移之比。由表1 可知：试件W1 和W2的延性系数分别为3.034和4.085，即二者均呈现出较好的延性和变形能力。

3.4 墙体侧向变形

如图1(a)和1(c)所示，沿墙体高度分别布置了3 个水平位移计，分别位于第1 条、第2 条水平条带截面中心及顶梁中心，距离墙底分别为0.72，1.52 和2.35 m。试件W1 和W2 各荷载特征值对应的侧向变形曲线如图6 所示，图中，H为墙体高度。由图6 可知：试件W1 和W2 的侧向变形曲线基本相似，在极限荷载前，沿墙体高度的侧向变形基本均呈弯曲型或直线型，与对应初始裂缝形态多为弯曲水平裂缝相吻合，即该阶段仍由砌块和暗骨架共同承受抗侧作用；由破坏荷载对应的侧向变形可明显看出：曲线呈剪切型特点，该阶段对应墙体已充分耗能，裂缝已得到充分发展，对应抗侧能力主要由芯柱和水平条带组成的暗骨架提供，墙体进入弱框架工作阶段。

3.5 刚度退化曲线

图7 所示为试件W1 和W2 的刚度退化曲线。由图7 可见：试件W1 和W2 的刚度退化趋势大致相同，总体趋势均为退化初期衰减较快，伴随位移的增大而减缓，墙体达到极限承载力之后，刚度退化趋势趋于平缓，无明显突变现象。在加载全过程中，相同侧向变形下，试件W1的刚度均比试件W2 的大，说明窗间墙越窄，其抗侧刚度越小。

表1 荷载及位移特征值Table 1 Characteristic values of loads and displacements

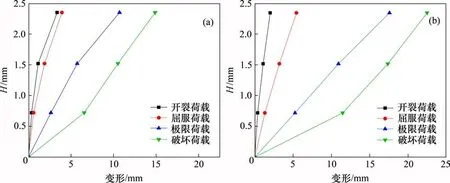
图6 墙体侧向变形Fig.6 Lateral deformation of walls

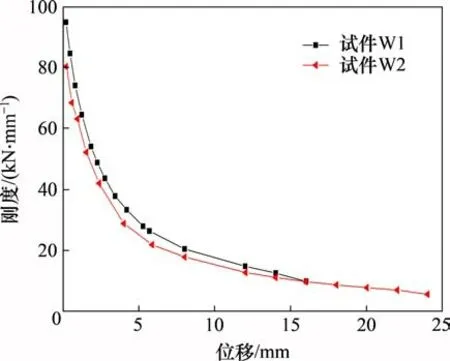
图7 试件刚度退化曲线Fig.7 Stiffness degradation curves of sample

3.6 能量耗散

结构或构件的耗能能力[12]是指在往复荷载作用下，结构或构件产生不可恢复的变形而吸收能量的能力，是衡量抗震性能的重要指标之一。采用滞回环面积S、能量耗散系数E和等效黏滞阻尼系数ζeq予以评价，表2 所示为试件W1 和W2 能量耗散系数与等效黏滞阻尼系数。

由表2 可知：随侧向变形增加，试件W1 和W2 的耗能能力均得到发挥，滞回环面积不断增大。在开裂和屈服荷载阶段，试件W1的滞回环面积显著大于试件W2的滞回环面积，这是对应的墙体耗能由暗骨架及其约束的砌块砌体共同承担，窗间墙变窄致使暗骨架约束的砌体面积减小所致；在极限和破坏荷载阶段，试件W1 和W2 的滞回环面积差不多，这是因为在后期破坏阶段，墙体耗能主要依靠暗骨架，且2片墙体对应的暗骨架几乎相同。

由表2 还可知：试件W1 的能量耗散系数和等效黏滞阻尼系数变化特点与试件W2的不同，前者对应的E和ζeq伴随侧向变形增加逐渐增大，即耗能能力不断增强；而后者对应的E和ζeq则呈现先降低后增大的现象，这是因为，在加载初期，对应屈服荷载阶段在第1道水平条带下方出现了水平裂缝滑移现象，使滞回环趋近于弓形且呈轻微“捏缩”现象，而在加载后期，随裂缝开展，墙体耗能得到显著增强。进一步对比分析试件W1 和试样W2的E和ζeq可知，除了在未充分耗能的开裂阶段，试件W1 的E和ζeq略小于试件W2 的E和ζeq之外，在后续各阶段，试件W1 的E和ζeq均显著大于试件W2 的E和ζeq，即窗间墙宽度变窄直接显著影响墙体后期耗能。

3.7 墙体失效机制

砌块与暗骨架的协同工作可以通过墙体立面同一位置二者的应力对比予以分析，图8所示为试件W1测点H10和试件W2测点H7处砌块和钢筋的实测应力。砌块和钢筋的应力分别由实测应变乘以相应的弹性模量(分别为9×109Pa 和2×1011Pa)求得。结合前文分析，并根据图8所示砌块与钢筋的实测应力对比可知：试验墙体的失效机制可分为共同工作、转化过渡和弱框架工作3个阶段。

1)共同工作阶段为从开始加载，到墙体出现第1 条水平裂缝。该阶段荷载-变形曲线近似为直线，墙体侧移和钢筋应力都比较小，并且钢筋与砌块的应力基本相同，二者能够共同工作。

2)转化过渡阶段为从墙体开裂到达到极限承载力。该阶段荷载-变形曲线由近似直线开始向曲线转变，墙体侧移逐渐增大，刚度不断减小，实测钢筋应力增长、砌块应力变化不大，即暗骨架相较于砌块已开始承担更大的抗侧作用，将此阶段定义为动态的转化过渡阶段。

3)弱框架工作阶段为从墙体极限承载力到最终破坏阶段。该阶段实测钢筋应力快速增长，相较于承受低应力水平甚至退出工作的砌块，抗侧已演变为由芯柱和水平条带组成的弱框架体系承担；对应荷载-变形曲线的下降段，墙体承载力不断下降，砌块出现破碎、剥落现象，主裂缝宽度明显增大。

4 抗震承载力计算方法

4.1 基于等效弹性板模型的开裂荷载计算

根据自保温暗骨架承重墙的受力特点可知，在墙体开裂前对应的暗骨架和砌块能够整体受力且共同工作，因此可将自保温暗骨架承重墙简化为图9所示的等效弹性板模型[13]，其内力计算符合线性叠加原理。

以最大拉应力理论[14]为基础，充分考虑开洞率及暗骨架的约束作用，建立带窗洞自保温暗骨架承重墙开裂荷载Vcr的计算公式：

表2 试件W1和W2的能量耗散系数与等效黏滞阻尼系数Table 2 Energy dissipation coefficient and equivalent viscous damping coefficient of specimens W1 and W2

图8 试件砌块和钢筋应力对比Fig.8 Stress comparison between block and steel

图9 等效弹性板模型Fig.9 Equivalent elastic slab model

式中：c为墙体开洞率，即窗洞与墙体的立面面积之比；ft为砌体抗拉强度，试验墙体取0.26 MPa；Aw为墙体水平向净截面面积；σq为砌块所受竖向压应力；dc为暗骨架对砌块的约束系数，墙体中水平条带和芯柱的数量越多，暗骨架对其约束作用越明显，墙体整体性亦越好，据参考文献[14]修正可得：

式中：k和j分别为芯柱、水平条带数量。

根据前文分析可知，开裂前砌块与暗骨架共同工作、变形协调，即：

又根据σq=Nq/(tbq)，σc=Nc/(tbc)，且N=Nq+Nc，其中，bq为水平方向的砌块长度；bc为混凝土长度；Nq和Nc分别为砌块砌体和混凝土芯柱承担的竖向力，可得：

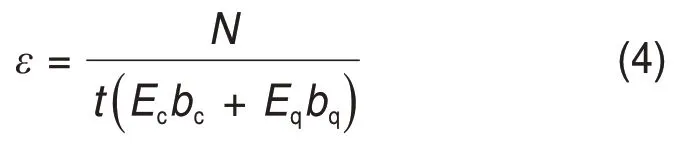
故

式中：N为墙体竖向轴力之和；t为墙厚；Eq和Ec分别为砌块砌体和混凝土的弹性模量。

按照上述方法计算可知，试件W1 和试件W2的开裂荷载分别为134.220 kN和105.095 kN，与实际测试值140.655 kN 和100.573 kN 相比，相对误差分别为-4.58%和4.50%，即修正建立的墙体开裂荷载计算方法具有较高精度。

4.2 基于抗剪抵抗机构的极限荷载计算

由墙体失效破坏模式可知，试件W1 和W2 最终破坏都是在暗骨架所包围的区域形成了阶梯状斜裂缝，据此并基于抗剪抵抗机构思想[15]构建刚架斜压杆模型，如图10 所示。该模型将暗骨架所包围的砌块砌体用1根沿其对角线放置的等效斜压杆代替，从而整片墙体的极限荷载Vmax由等效斜压杆、水平条带、竖向芯柱所组成的抗剪抵抗机构共同承担，对应计算公式为

式中：V1为水平条带内钢筋的抗剪承载力；V2为竖向芯柱提供的销栓力；V3为等效斜压杆承担的抗剪承载力。

图10 刚架斜压杆模型Fig.10 Baroclinic bar model of rigid frame

4.2.1 水平条带内钢筋的抗剪承载力V1

根据GB 50011—2010“建筑抗震设计规范”[5]确定水平条带内钢筋的抗剪承载力，即：

式中：ζs为钢筋参与工作系数，取0.138；fyh为水平条带内钢筋的抗拉强度设计值；Arh为水平条带内钢筋的截面面积之和。

4.2.2 竖向芯柱提供的销栓力V2

竖向芯柱提供的销栓力V2据文献[16]修正，即：

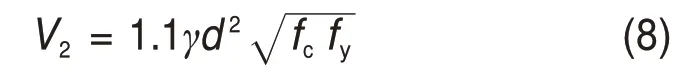
式中：γ为墙体中芯柱的根数；d为芯柱钢筋直径；fc为芯柱混凝土的轴心抗压强度设计值；fy为芯柱钢筋的抗拉强度设计值。

4.2.3 等效斜压杆承担的抗剪承载力V3

根据参考文献[17]修正可得：

式中：αfm为斜压杆的有效抗压强度，α为斜压杆有效强度系数(取值0.073)，fm为灌芯砌体平均抗压强度(取值11.37 MPa)；θ为等效斜压杆倾角，即斜压杆与水平面之间的夹角；Astr为等效斜压杆的截面积：

式中：w为等效斜压杆的截面宽度，采用等效刚度法确定，即利用共同工作阶段抗侧刚度Ke与转化过渡阶段的初始抗侧刚度Ks相等的特点确定。

1)共同工作阶段抗侧刚度Ke的计算。参考文献[18]，充分考虑墙体带窗洞及砌块有孔洞的特点，修正可得：

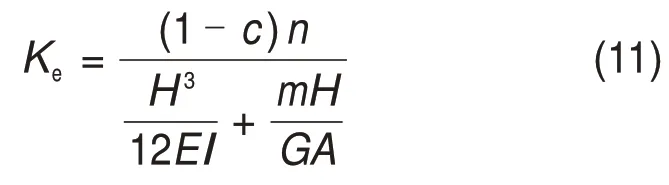
式中：n为刚度折减系数，取值0.125；m为截面剪应力分布不均匀系数，取值1.2；A为未开洞墙体的水平横截面面积；I为墙体截面惯性矩；E为墙体的弹性模量，E=ηVcEc+VqEq[19]，η为混凝土纤维修正系数(取值0.7)，Vq和Vc分别为砌块和混凝土的体积分数；G为墙体的剪切模量，1/G=Vc/Gc+Vq/Gq，Gq和Gc分别为砌块和混凝土的剪切模量[19]。

据式(11)计算可得，试件W1 和试件W2 的抗侧刚度Ke分别为86.5 kN/mm 和77.660 kN/mm，与对应的实测刚度94.804 kN/mm 和80.216 kN/mm 相比分别小8.76%和3.19%，计算精度较高。

2)转化过渡阶段初始抗侧刚度Ks的计算。等效斜压杆的轴向压缩如图11 所示。根据单刚架模型类比思想计算Ks，即假定水平集中力P使单刚架模型产生单位位移δ，则P等于墙体的抗侧刚度。

当刚架产生单位水平位移δ，斜压杆的轴向压缩Δ=δcosθ≈cosθ=l-l′，其中，l′为变形后的斜压杆长度。

斜压杆的轴向压力N1=Pcosθ，且N1=因此，

从而可得单刚架的抗侧刚度为

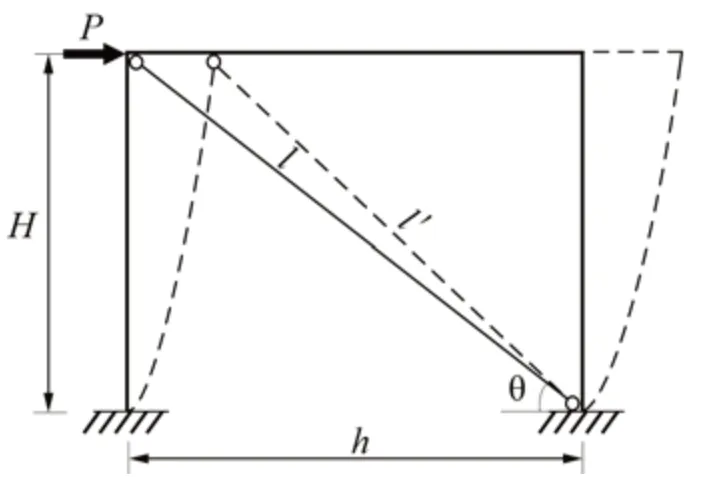
图11 等效斜压杆的轴向压缩Fig.11 Axial compression of equivalent baroclinic struts

对应试验带窗洞墙体的抗侧刚度计算公式为

式中：Ksxy为计算模型中第x跨第y层的单个刚架的抗侧刚度。

令Ke=Ks，计算求解可得等效斜压杆的截面宽度w，从而可得V3和Vmax。

结果表明，试件W1 和试件W2 的抗剪极限承载力分别为162.084 kN 和145.682 kN，与实测值178.153 kN 和157.686 kN 相比分别小9.02% 和7.61%，计算方法偏于安全且精度较高。

4.3 带窗洞墙体极限承载力的剪力分配

带窗洞自保温暗骨架承重墙的极限承载力由窗间墙和窗下墙共同提供，其各自承担剪力可据4.2 节建立的计算方法分别确定，表3 所示为试件W1 和试件W2 对应的窗间墙和窗下墙所承担的剪力。

由表3 可知：试件W1 和试件W2 对应窗间墙承担的极限抗剪承载力分别为147.746 kN 和130.146 kN，后者较前者下降约11.91%；试件W1和试件W2对应窗下墙承担的极限抗剪承载力分别为14.338 kN 和15.536 kN，试件W2 较试件W1 提高约8.36%，即随窗洞增宽，窗间墙和窗下墙承担的极限抗剪承载力分别呈下降、上升特征，但窗下墙的绝对或相对增幅均低于窗间墙的降幅，墙体总的抗剪极限承载力呈下降趋势。进一步分析可知，试件W1窗间墙和窗下墙承担的剪力占比分别为91.15%和8.85%；试件W2窗间墙和窗下墙承担的剪力占比分别为89.34%和10.66%，即2 片墙体窗间墙、窗下墙承担的剪力占比基本不因窗洞尺寸的变化而显著变化，分别占比约90%和10%。

表3 带窗洞墙体极限承载力剪力分配Table 3 Shear distribution of the wall with windows

综上可知，窗间墙在承担极限抗剪承载力方面起主导作用；但窗下墙作为墙体抗震的第一道防线，在抗震设计与分析时应考虑其影响。

5 结论

1)带窗洞自保温暗骨架承重墙具有良好的抗震性能，试件W1 和试件W2 均为延性破坏，对应延性系数分别为3.034和4.085；其失效过程可划分为共同工作、转化过渡和弱框架工作3个阶段。

2)基于等效弹性板模型，建立了带窗洞自保温暗骨架承重墙开裂荷载的计算方法；基于抗剪抵抗机构思想提出了带窗洞刚架斜压杆模型，建立了墙体极限荷载的计算方法；计算值与实测值相比表明，所建立的理论计算方法精度较高。

3)窗下墙先于窗间墙破坏，窗下墙为带窗洞自保温暗骨架承重墙的第一道抗震防线；窗洞宽度对墙体的滞回曲线、骨架曲线、刚度及其退化、耗能能力等均存在显著影响；窗间墙在承担抗震极限承载力方面起主导作用(约占90%)，但不能忽略窗下墙对带窗洞墙体抗震性能的影响。