基于DFOWA算子的动态三参数区间灰数多属性决策
胡经涛,王应明
(福州大学 经济与管理学院,福建 福州 350116)
多属性决策可以简单理解为按照一定的决策准则,对有限的备选方案计算不同属性下的属性值,并进行排序和选择该准则下的最优方案,在经济、管理、军事、建筑工程等领域有着重要的应用,排序准则的确定则是多属性决策的关键,也是众多研究的热点[1]。由我国学者邓聚龙教授提出的灰色系统理论[2],可从不同角度去描述和处理各种不确定信息,产生了巨大的国际影响力,灰关联决策法在决策信息、决策模型等方面经过不断发展已经成为不确定多属性决策的重要组成部分[3-4]。灰数则是灰色系统理论中的基本单元,有一定的取值范围但不能确定具体数值,是可以对其进行加工、运算生成得到有意义有价值的信息,从而描述系统。
灰关联模型虽已采取区间灰数对属性值做出改进,但区间数存在着为完整保留属性信息而导致区间过大、默认区间内各值概率相等的缺点,且随着运算法则的计算会产生误差甚至失真现象。为此,张东兴等[5]考虑了具有“奖优罚劣”线性变换算子的基于前景理论的灰关联决策方法;陈可嘉等[6]给出了三参数区间灰数距离测度与排序方法,考虑三参数区间灰数重心点的影响,提出了基于三参数区间灰数的TOPSIS决策方法。然而,大多数文献研究的是单一时间点的静态决策问题,但是实际问题中很多领域需要考虑的是多时段动态的决策过程,如动态投融资金[7]、线上评估、股票交易、军备系统等。为了使数据全面反映决策对象的特征,得到更加合理的决策结果,一些学者开始研究动态多属性决策问题。如裴凤等[8]针对灰数与模糊数混合的动态多属性问题,考虑了决策问题发展的多阶段性,采用熵权法确定时间权重,提出了基于时间参照点的混合靶心模型;陈德江等[9]采取泊松分布赋权法对多时段目标信息进行融合,从而确定动态威胁排序结果。但是对于动态的时间权重大多是直接给出或者由决策者直接设定[10-11],这会导致决策结果受人为因素影响。
因此,笔者针对各决策时段时间权重、属性权重信息未知的情况,首先,改进了传统灰数距离测度公式中,仅考虑端点值的差异造成信息缺失的不足,给出了一个保留区间灰数信息特性且具有更好分辨性能的新距离测度公式;其次,给出一个动态模糊有序加权平均算子(DFOWA),利用该算子对各备选方案进行方案内属性间与方案间多时段两次信息集结,很大程度减少了主观因素的影响,可对方案所有信息进行集结;最后,根据综合评价值的大小对各方案进行择优,并通过算例分析来验证该方法的科学有效性。
1 预备知识
1.1 三参数区间灰数

定义2[13]对于三参数区间灰数a(⊗)和b(⊗),这两个灰数的距离如式(1)所示,并满足以下性质:①非负性,d(a(⊗),b(⊗))≥0;②对称性,d(a(⊗),b(⊗))=d(b(⊗),a(⊗));③三角不等式,d(a(⊗),b(⊗))≤d(a(⊗),c(⊗))+d(c(⊗),b(⊗))。
d(a(⊗),b(⊗))=
(1)
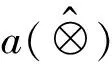
(2)
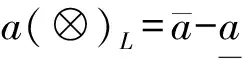

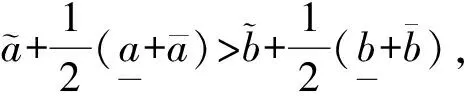
1.2 三参数区间灰数比较的可能度[16]
对于三参数区间灰数a(⊗)和b(⊗),称p(a(⊗)≥b(⊗))为a(⊗)≥b(⊗)的可能度,其中μ为风险系数。当μ=0.5时,表明决策者是风险中立型;当0<μ<0.5时,表明决策者是风险偏好型;当0.5<μ<1时,表明决策者是风险规避型。
p(a(⊗)≥b(⊗))=
(3)
将三参数区间灰数两两比较得到可能度矩阵P=(pii′)m×m,并利用式(4)求得排序向量:
(4)
2 决策方法
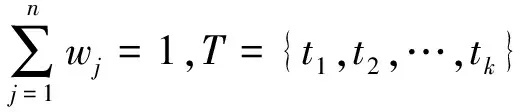
对于效益型属性有:
(5)
对于成本型属性有:
(6)
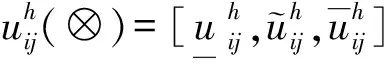
2.1 改进的三参数区间灰数距离公式
式(1)表示的距离公式通过引进心理风险系数来确定,但是并没有体现出灰数与区间数或者三角模糊数的区别,闫书丽等[17]定义两个三参数区间灰数的距离为:

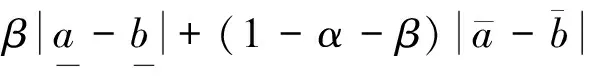
(7)
其中,0≤α≤0.5,0.5≤β≤1。
该公式主要是从三参数区间灰数的信息域和最大可能值出发,考虑绝对差值,不考虑区间内的每一个数值,与一般的区间数运算并没有本质区别,仅考虑端点值的差异影响,容易造成信息缺失,没有体现出信息背景下灰数不确定性的根本性特征。因此,笔者针对以上距离的不足,考虑三参数区间灰数信息域、核及区间内的每一点的差异,同时过滤区间灰数信息重合部分,最大化突出区间灰数间差异性,给出一种改进的三参数区间灰数距离公式,如式(8)所示,且该距离公式满足定义2中的3条性质。
(8)
2.2 属性权重的确定
求解方案的综合属性值,并按照大小进行排序,是方案选择时的重要手段。如果某一属性对所有方案的综合属性值的排序影响不明显,则说明该属性对所有方案的综合属性值排序来说不是特别重要,即该属性仅对方案造成很小或有限的影响。因此,从对方案进行排序的合理性和客观性角度出发,那些对方案属性值影响越大的属性应该被赋予更大的权重。
对于规范化后的决策矩阵R=(rij)m×n,将属性Cj下决策方案Ai与其他方案之间的离差用Vij(w)来表示,并定义为:
(9)
用Vj(w)表示在属性Cj下所有方案与其他方案的总离差,可定义为:
于是,求解加权向量W可以转化为求解下列最优化问题:
则归一化后属性权重的计算公式为:
(12)
2.3 时间权重的确定
目前确定时间权重的主要方法有BUM法、厚今薄古法[18]、正态分布法、衰减法[19]等,由于时代的瞬息万变且信息更新的速度快,以往的数据可能不具有很好的代表性,但依然存在参考价值。根据灰色系统理论中“新信息优先”原则,基于熵值理论确定时间权重,具体定义如下:
(13)
式中:λh表示第h个时段的权重,表明了决策者对时序的重视程度;θ∈[0,1]表示的是“时间度”概念,θ越接近1表示决策者在所有时期数据中越重视距现在较远期的数据,θ越接近0意味着决策者在所有时期数据中越重视近期数据。θ的取值通常为0.1,0.2,0.3,0.4,0.5。当θ取0.5时,表明决策者对于各个时间段的数据无偏好,同样重视。
2.4 动态模糊有序加权平均算子(DFOWA)
2.4.1 有序加权平均算子(OWA)

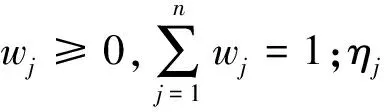
定义8设a(⊗),b(⊗),…,z(⊗)是一组三参数区间灰数,则DFOWA算子可分为方案内属性间集结与方案间多时段集结两步。
(1)方案内属性间集结:
DFOWAw(a(⊗),b(⊗),…,z(⊗))=
(14)
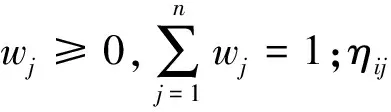
(2)方案间多时段集结:
(15)

3 算例分析
3.1 问题描述
假设由于业务扩展,某公司需要聘请一名分公司经理,目前共有4名候选人(x1,x2,x3,x4)。面试分为初面(t1)、复面(t2)、终面(t3)3个时间段。为了招聘到最合适的人选,决策者主要从以下几个方面考虑:自信程度(c1)、人际交流(c2)、工作热情(c3)、期望工资(c4) 。其中属性值采取三参数区间灰数来表示,决策者面试后得到初面、复面、终面各阶段的成绩表,如表1所示。
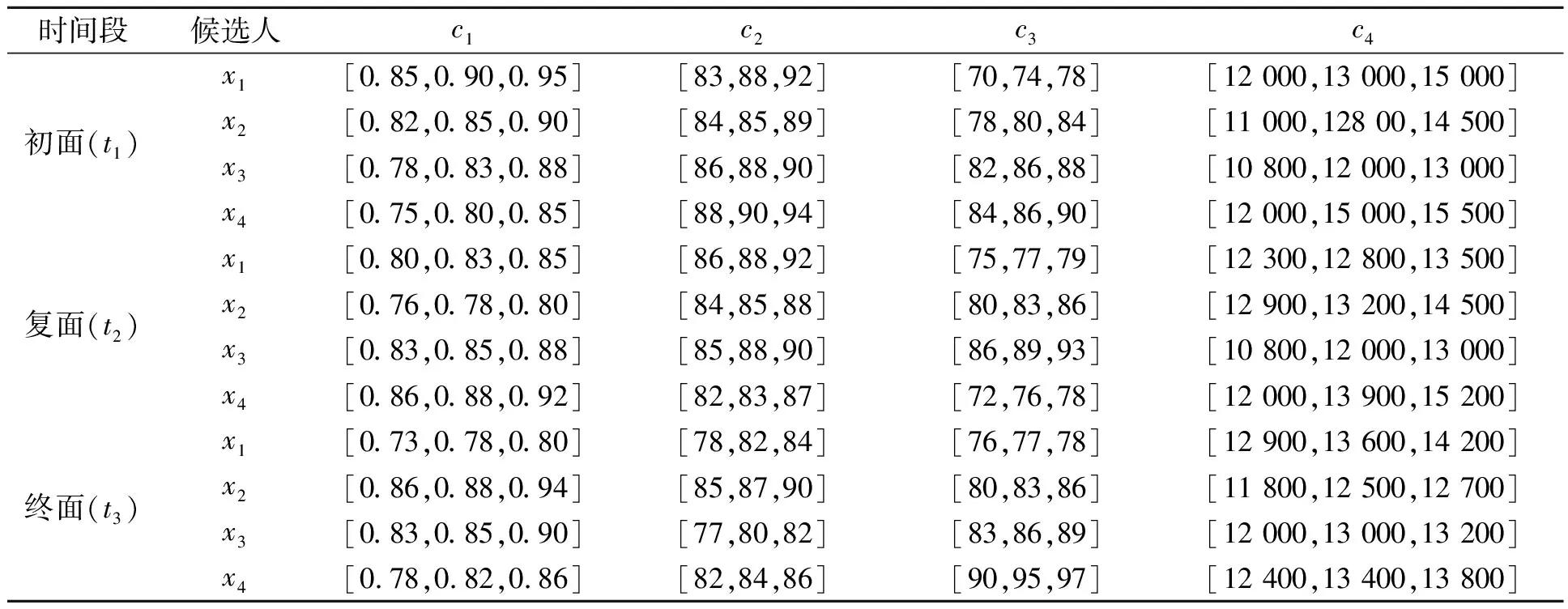
表1 各阶段成绩表
三参数区间灰数下的多属性决策方法的具体步骤如下。
(1)根据式(5)和式(6)将t1时段的初始决策矩阵进行规范化处理(以t1时段为例),得到U(t1)。
(2)利用改进的距离公式计算t1时段下的距离矩阵,并根据式(12)计算各属性权重:w1=0.236 3,w2=0.225 4,w3=0.280 6,w4=0.257 7。
(3)根据式(13)计算各时段权重,根据以往招聘数据反馈,令时间度θ=0.3,明显重视近期数据,得时间权重:λ1=0.154,λ2=0.292,λ3=0.554。

对方案间多时段集结可得各方案综合属性值:F1=(0.185 0,0.395 9,0.576 8),F2=(0.263 1,0.404 2,0.640 8),F3=(0.251 5,0.471 7,0.643 7),F4=(0.291 6,0.523 9,0.749 1)。
(5)根据式(3)计算两两三参数区间灰数比较的可能度,并求得可能度矩阵:

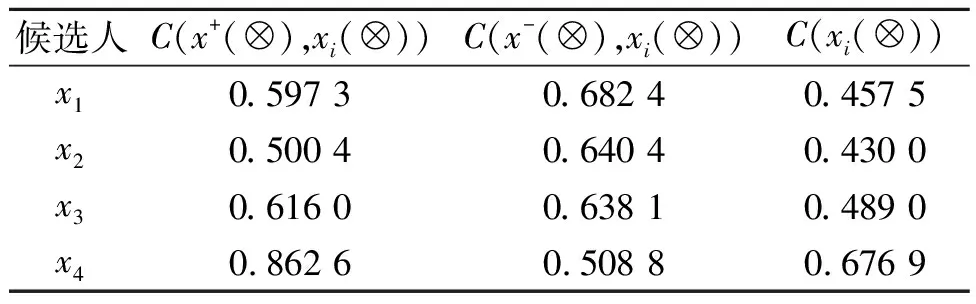
(6)根据式(4)计算各方案综合评价值:T1=0.199 6,T2=0.233 3,T3=0.259 6,T4=0.307 5。可以看出T1 (7)调整时间度θ取值并计算各时段权重,得到各应聘者最终排序,如表2所示。 表2 不同时间度下的综合评价值及排序结果 由表2可知,当θ=0.9时,意味着决策者极其重视该公司距今久远的招聘数据,候选人排序先后顺序发生了改变,说明该公司的招聘原则可能发生了变化,就会产生不同结果,这对解决实际问题具有现实意义。 为了说明所提方法的科学性与有效性,将所得结果与其他两篇文献方法进行对比分析。 由表3可知,各应聘者的排序为x2 (2)前景理论下的三参数区间灰数决策法(文献[13]):该方法考虑了时间权重的波动性,将两两方案互相比较求解其间距离来确定最优属性权重,最终计算得出综合前景值。求得的最优属性权重w*=(0.219 1,0.188 5,0.334 0,0.258 5);最终综合前景值为:T1=-2.104 1,T2=-0.766 3,T3=-0.419 0,T4=0.712 1,因此各应聘者的排序为x1 表3 决策向量的区间关联度 在信息获取时用三参数区间灰数来描述决策信息更符合投融资、管理、大工程等实际情况,考虑时段权重的动态性也是实际问题发展的需要。因此,笔者提出了一个新的基于三参数区间灰数的距离测度公式和基于DFOWA算子的三参数区间灰数信息下的动态多属性决策方法。一方面利用核和信息域最大程度保留三参数区间灰数特性,另一方面利用DFOWA算子进行方案内属性间与方案间多时段两次集结,很大程度减少了主观因素的影响,对方案所有信息进行了集结。最后通过算例分析与不同方法比较,验证了所提方法的科学可行性。未来研究可更多考虑既有区间灰数又有实数的决策情形及更为复杂的四参数区间灰数动态多属性决策模型。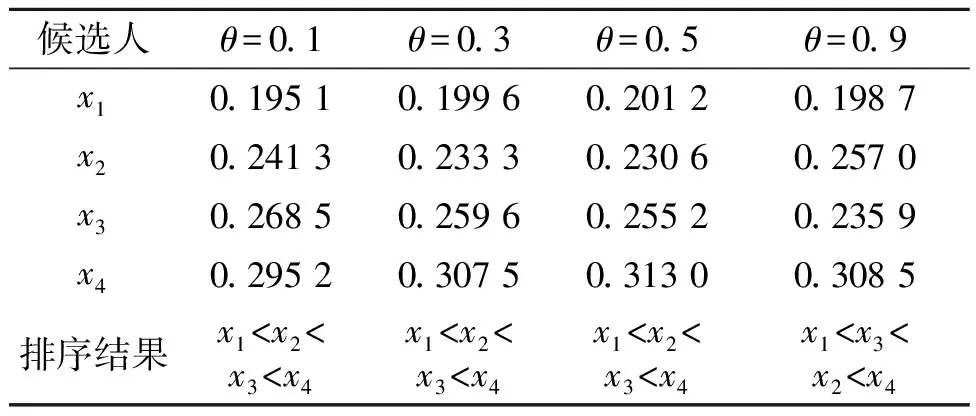
3.2 方法比较
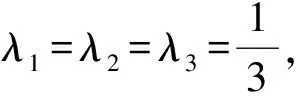
4 结论

