任务可选的自动化集装箱码头AGV配对调度优化
包晓琼,鹿飞燕,胡志华
(1.上海海事大学 物流研究中心,上海 201306;2.上海海事大学 电工电子实验中心,上海 201306)
自动化集装箱码头中最主要的3类作业设备为自动化岸桥、自动化堆垛机、自动化导引车(automatic guided vehicle,AGV)。通常,一台40 ft的AGV可以运输两个20 ft的集装箱或一个40 ft的集装箱,而这种配置在运输单个20 ft的集装箱时装载率为50%,意味着资源浪费。因此,采用20 ft的AGV独立运输20 ft的集装箱和配对运输40 ft的集装箱是自动化集装箱码头的一种新工艺,然而这种新工艺对配对调度提出了更高的要求[1-2]。
AGV是自动化集装箱码头中最常见的水平运输设备[3]。目前AGV调度[4-5]与路径优化[6]的研究较多,其他也包括AGV配置问题[7]和充电问题[8]。HU等[9-10]从船舶分段运输和大件物流运输模式中得到启发,提出多辆车运输一个货物的多车辆单任务问题(multi-vehicle and one-cargo transportation,MVOC),建立混合整数规划模型并设计贪婪算法和改进遗传算法求解。AGV配对调度就是一个MVOC问题。
笔者采用20 ft AGV独立运输20 ft集装箱和配对运输40 ft集装箱的新工艺,考虑任务可选模式下,按照对入选的任务进行奖励、对延后执行的任务进行惩罚的策略,研究AGV配对调度问题。将搬运成本和惩罚成本作为约束条件,以运输成本、完成时间和空载时间最小化为目标,建立混合整数规模模型。设计算例并对AGV数量、运输时间和操作时间3个参数进行敏感性分析,以验证模型的有效性。
1 问题描述
车辆资源有限且集装箱装卸搬运作业密集是自动化集装箱码头建设进程中的常见问题。在计划期内考虑任务可选,入选的任务有搬运成本,而被延后执行的任务会产生惩罚成本。由20 ft AGV独立运输20 ft集装箱和配对运输40 ft集装箱优先任务的关键点是配对调度。配对调度分为3个步骤:①选择配对,令选中的AGVs行驶至任务装载点,配对成具有相应荷载能力的搬运车。②搬运,配对AGVs将集装箱从装载点搬运到卸载点。③分离,卸载结束后,配对AGVs自动分离,等待后续作业命令。
在任务可选模式下,采用奖惩策略,并以搬运成本和惩罚成本为约束条件,建立混合整数规划模型,为优先任务匹配AGV配对调度方案。假设总任务集合中有6个搬运任务,每个搬运任务对应一个集装箱,集装箱尺寸Si、相应的装载点Pi和卸载点Di均已知。由于集装箱尺寸、装卸载点位置和起重机操作时间的差异,各任务运输成本不同,运输成本包括搁置成本和搬运成本。以最小化运输成本为目标,从6个搬运任务中选中3个优先任务,分别为1、3、5。引入2个虚拟任务:起点任务S和终点任务T,则优先任务共5个。任务1中集装箱尺寸为40 ft,需要2辆AGV配对搬运;任务3和任务5中集装箱尺寸为20 ft,由1辆AGV可完成搬运,配对调度示意图如图1所示。
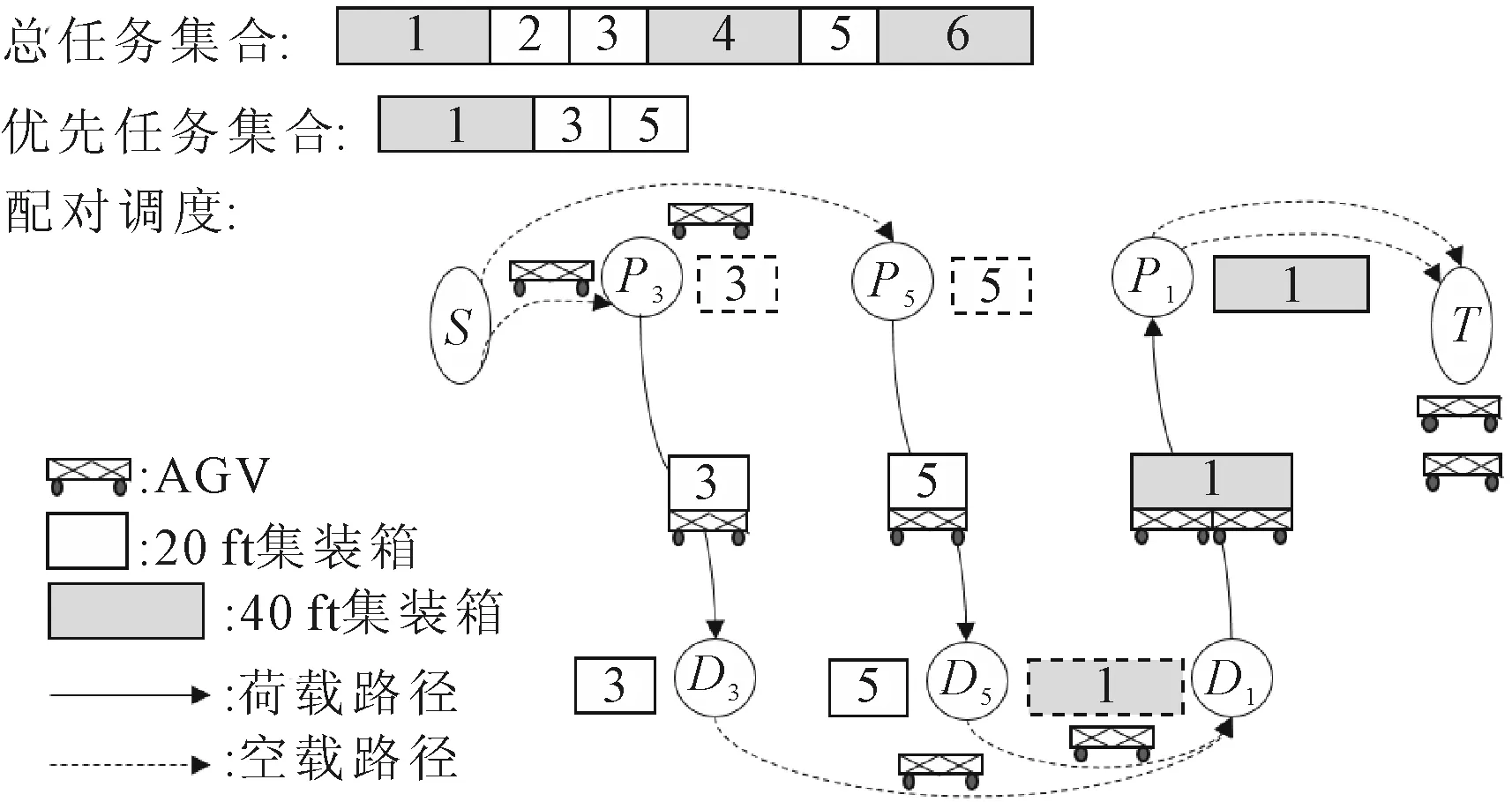
图1 AGV配对调度示意图
为便于建模,提出以下假设:①搬运任务尺寸及装卸载位置信息确定。②AGV数量、位置信息及可调度时间确定。③AGV配对和分离时间忽略不计,在装载操作开始之前,AGV需完成配对并等候;卸载操作结束之后,配对的AGV方可分离。④排除搬运过程中交通堵塞、电量不足等不确定因素。⑤AGV全程无故障,匀速行驶且忽略启动时间。
2 任务可选的配对调度模型
(3)决策变量。yi∈{0,1},1表示任务i为优先任务,产生搬运成本,0表示任务i为搁置任务,产生搁置成本;xijv∈{0,1},1表示第v辆AGV优先搬运任务i后紧接着搬运任务j,否则为0,v∈V;yiv∈{0,1},1表示第v辆AGV有参与搬运任务i;zi表示任务i的可操作时刻。
(4)目标函数及约束条件。在20 ft自动化导引车(AGV)独立搬运20 ft集装箱和配对搬运40 ft集装箱的自动化集装箱码头新工艺背景下,以最小化优先任务的运输成本、完成时间和空载时间为目标(如式(1)~式(4)所示),建立任务可选配对调度的混合整数规划模型。式(5)和式(6)表示任务i的完成时间应晚于准备时间且非负;式(7)规定了AGV服务的首个任务i的完成时间;式(8)表示AGV合理分配任务并明确其服务顺序;式(9)~式(11)表示为优先任务分配的AGV数量应与集装箱尺寸相一致,否则任务不能被处理,一直处于等待状态;式(12)为作业流约束,即入度与出度相等;式(13)和式(14)表示虚拟起点和虚拟终点是AGV服务的初始任务和末任务。
minf=(fCost,fMakespan,fEmpty)
(1)
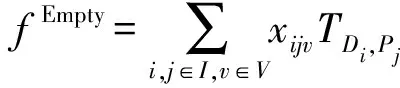
(3)
fMakespan≥zi,∀i
(4)
f≥0,zi≥0,∀i
(5)
zi≥Ai,∀i
(6)
zi≥Rv+TLv,Pi+Ti,∀i,v
(7)
zj+(1-xijv)M≥zi+Tj+TDi,Pj,∀i≠j,v
(8)
(9)
(10)
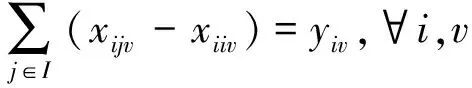
(11)
xijv+xjiv≤1,∀v
(12)
(13)
(14)
3 算例分析
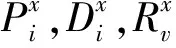
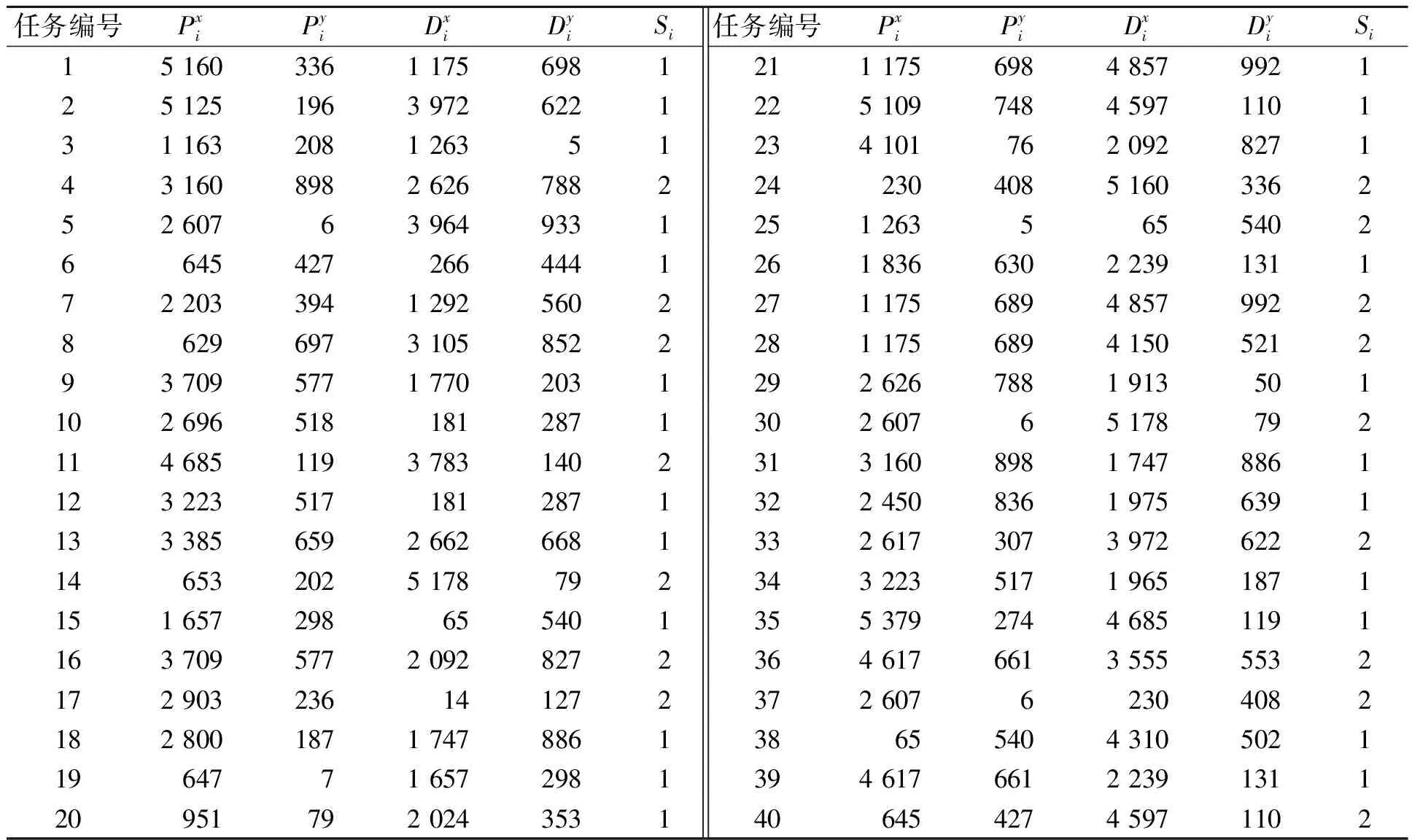
表1 搬运任务参数值

表2 AGV参数设置
采用GUROBI求解器,使用PYTHON语言编译求解模型,得到3个算例的最优作业序列及运输成本、完成时间和空载时间。算例1的AGV配对时序图如图2所示,其中矩形区域中的数字表示AGV正在完成的任务序列,矩形的长度表示时间的长短。算例2和算例3的AGV作业衔接序列如表3和表4所示。
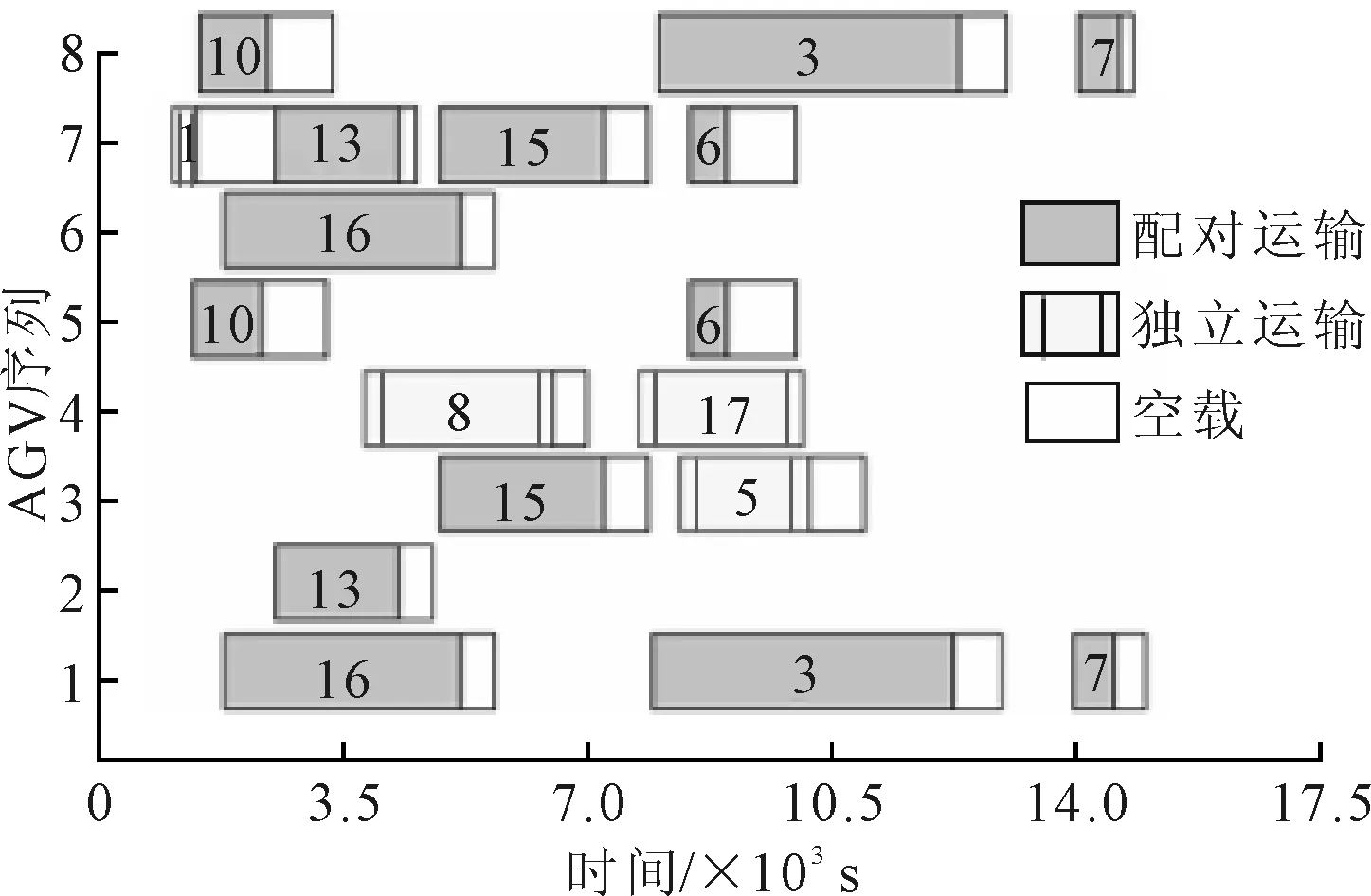
图2 算例1的AGV配对时序图
算例1从20个总任务集合中选中13个优先任务(包含2个虚拟任务),其中20 ft集装箱共4个(任务编号为1、5、8、17),40 ft集装箱共7个(任务编号为3、6、7、10、13、15、16),由8辆AGV搬运优先任务的完成时间为37 206,运输成本为61 188。例如7# AGV的搬运任务有4个,即独立运输任务1,分别与2#、3#和5# AGV配对搬运优先任务13、15和6。
算例2由9辆AGV 配对完成23个优先任务,包括8个20 ft集装箱和15个40 ft集装箱,完成时间为45 292,运输成本为108 719。
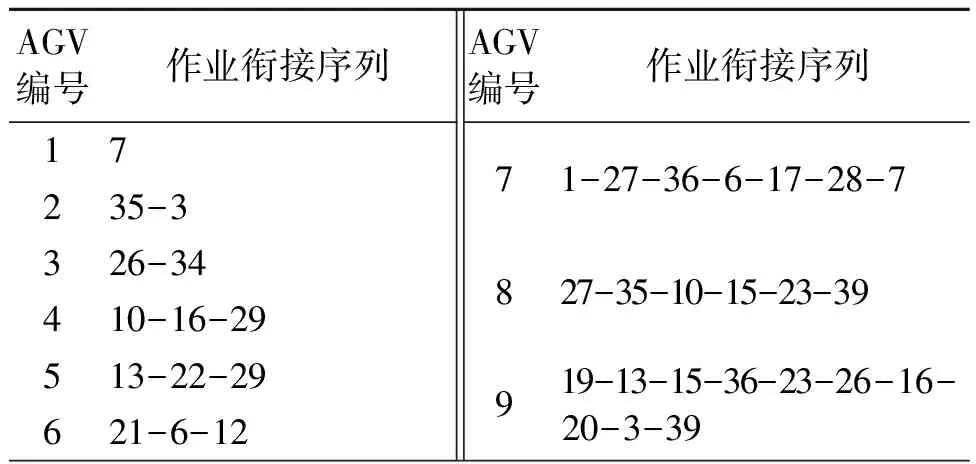
表3 算例2 的AGV作业衔接序列
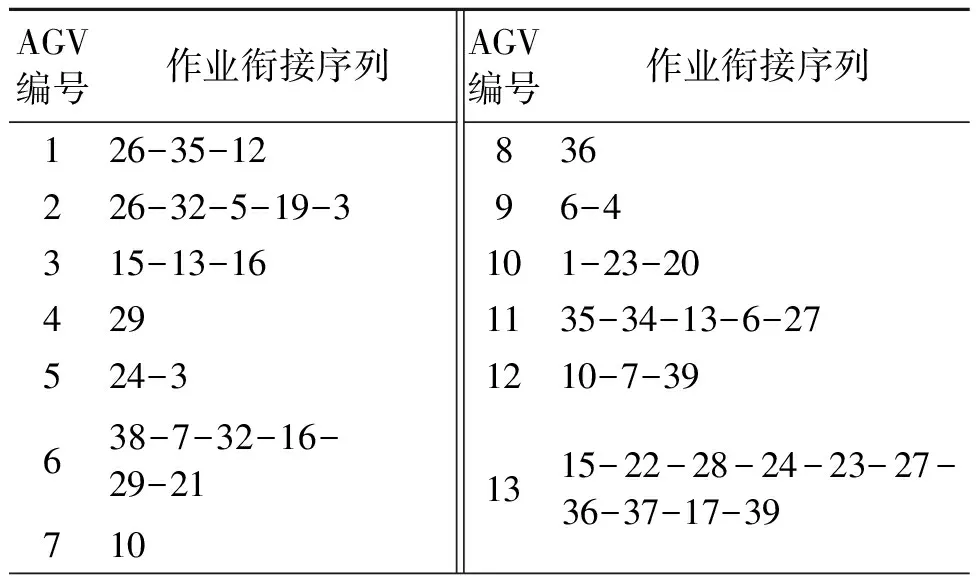
表4 算例3的AGV作业衔接序列
算例3从40个总任务集合中选中28个优先任务,包括13个20 ft集装箱和15个40 ft集装箱,并由13辆AGV 配对搬运,完成时间为26 784,运输成本为106 881。
4 实验验证
在算例3(40个搬运任务20辆AGV)的基础上设计3组实验场景,以研究AGV数量、运输时间和操作时间的敏感性并分析模型的特征。场景描述及参数调整如表5所示。
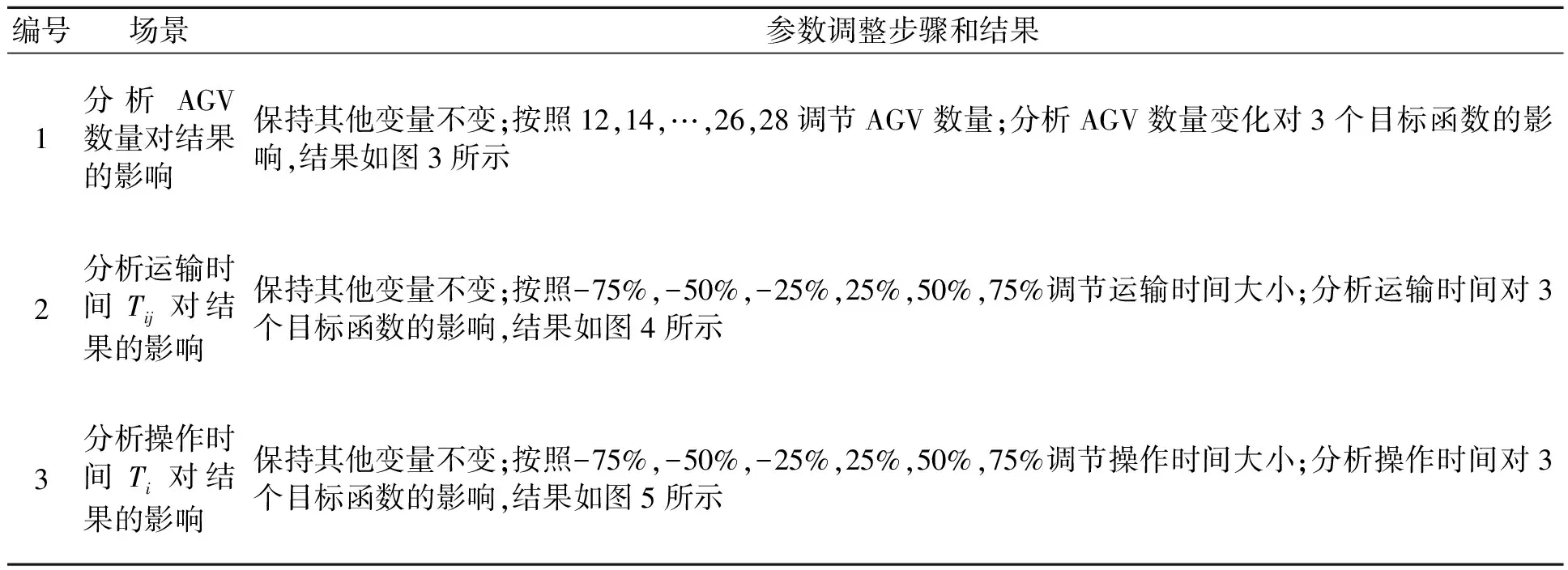
表5 实验场景和参数调整
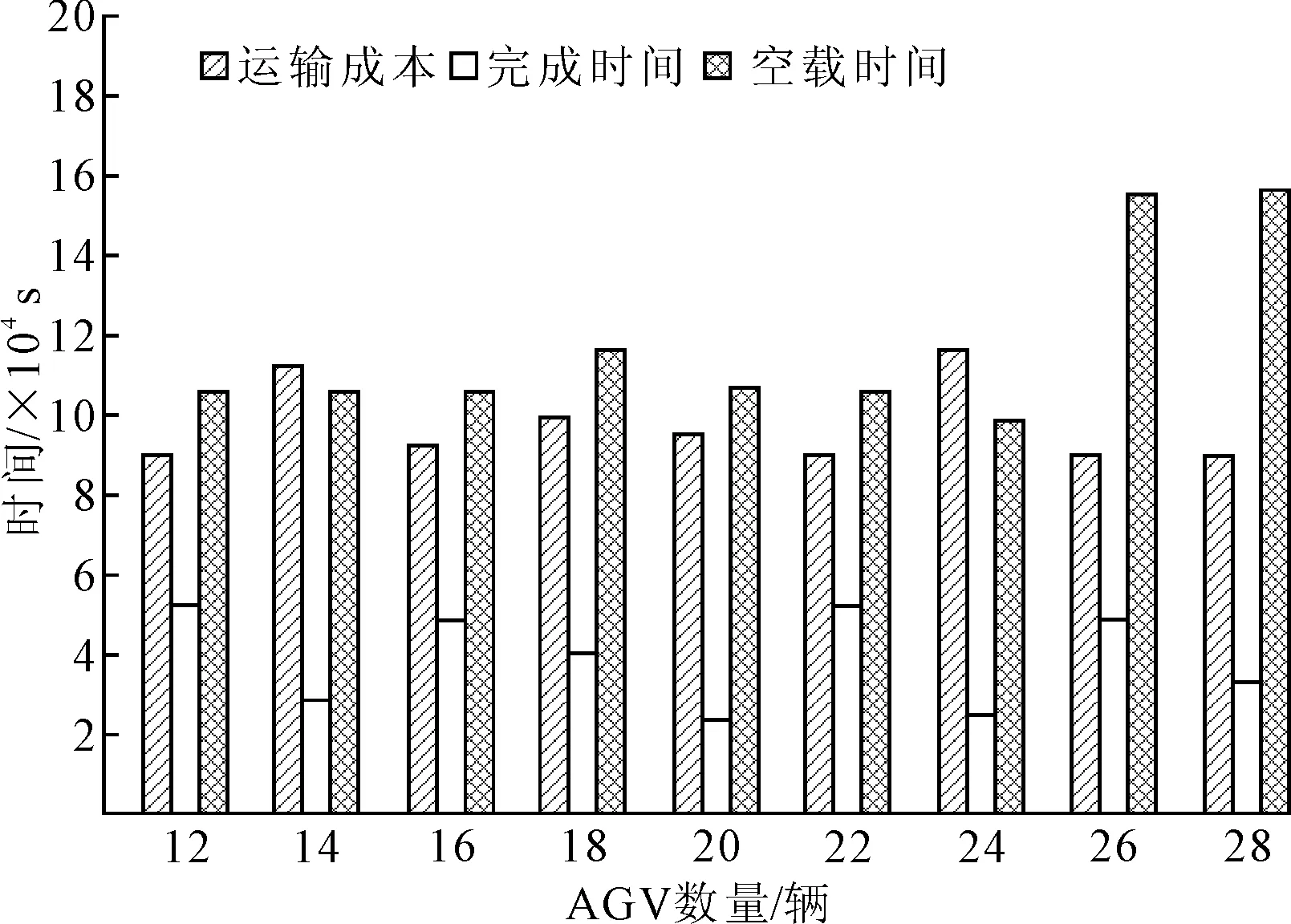
图3 AGV数量变化对结果的影响
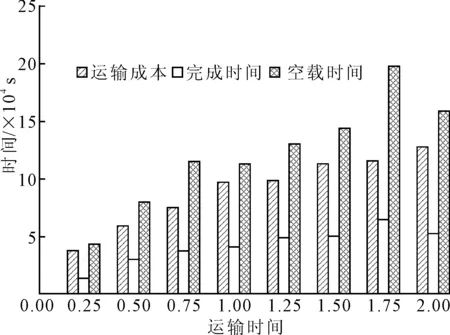
图4 运输时间Tij变化对结果的影响
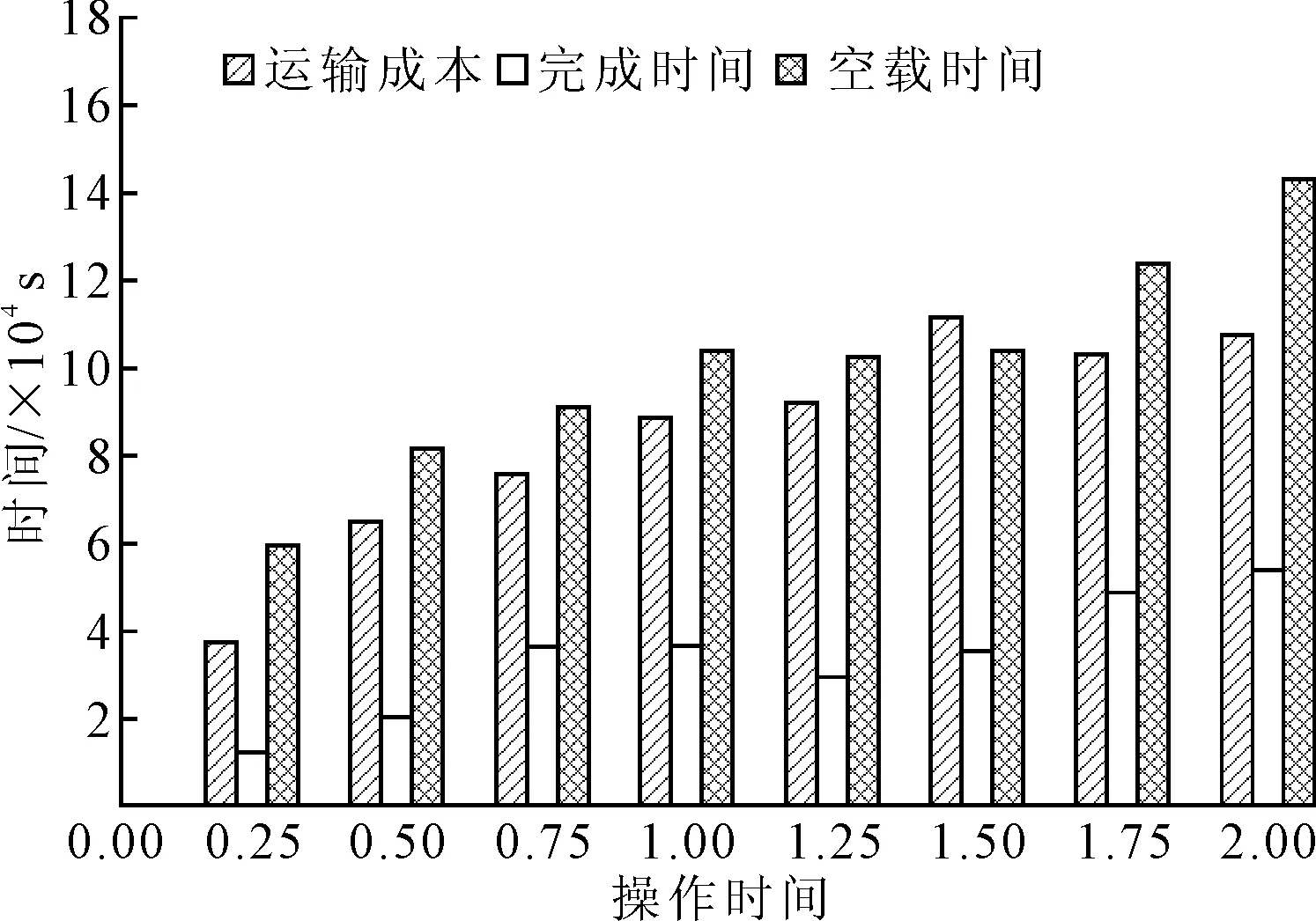
图5 操作时间Ti变化对结果的影响
(1)AGV数量变化对结果的影响。由图3可知,运输成本和完成时间呈波动逆向变化,即运输成本增加时,完成时间相应减少。当AGV数量处于12~20辆时,运输成本和完成时间之和波动下降。当AGV配置数量达到20辆时,运输成本和完成时间之和最小;当AGV数量在12~16辆之间时,空载时间变化较小,之后波动下滑,但当AGV数量达到26辆时,空载时间显著增加。根据以上分析,以运输成本、完成时间和空载时间为指标,以搬运成本和搁置成本为约束,可为搬运任务匹配合理的AGV数量。
(2)运输时间变化对结果的影响。由图4可知,随着运输时间的增加,运输成本逐步增加,完成时间和空载时间呈波动增加,在运输时间为初始值时空载时间略有下降。完成时间对运输时间变化的敏感性较低,可知在搬运成本和搁置成本约束条件下,该算法可以最优的匹配方式调度AGV搬运待完成任务。
(3)操作时间变化对结果的影响。由图5可知,随着操作时间的增加,运输成本、完成时间和空载时间均波动上升。相较于实验场景2,运输成本和空载时间对操作时间变化的敏感性均增强。
5 结论
采用由20 ft的AGV独立运输20 ft集装箱和配对运输40 ft集装箱的新工艺,在车辆资源有限且集装箱装卸搬运作业密集的环境中,考虑计划期内选择部分任务优先完成,并对延后的任务进行惩罚。以搬运成本和搁置成本为主要约束条件,以运输成本、完成时间和空载时间最小化为目标建立混合整数规划模型。设计自动化集装箱码头算例和数据集,研究AGV数量、运输时间和操作时间的敏感性,结果表明运输成本对操作时间和运输时间敏感性较低,而完成时间和空载时间对这两个参数敏感度较高,且空载时间对两个参数的敏感性比完成时间高。以上实验验证了模型的有效性,并可获得合理的配对调度方案,具有良好的可行性,对降低成本、提高码头效益也具有实际意义。

