改进的哈希学习高效推荐算法

应文杰，桑基韬

北京交通大学 计算机与信息技术学院，北京100044

1 引言

个性化推荐技术由于能为用户推荐感兴趣的内容，提高用户体验，进而增强用户粘性以及用户的忠诚度，已经得到许多大型互联网公司（如Amazon、Alibaba、Baidu等）的广泛关注和深入研究[1-2]。然而，随着互联网的快速发展，各行各业的数据都呈现爆炸式的增长。例如，截止到2018 年10 月，Taobao 平台上已经有超过5 亿的用户和10 亿的商品。因此，推荐系统也面临着数据存储和检索效率等挑战[3-5]。

哈希学习通过保持原始空间中的近邻关系将原始数据映射成二进制码的形式。有效地减少数据存储开销，加快相似性检索效率而广泛地应用于信息检索、计算机视觉、推荐系统等领域[6-10]。最近，一些基于哈希学习的推荐方法被应用于提高推荐系统的效率[11-15]。这些方法的核心是将用户评分矩阵看作用户与项目之间的相似性矩阵，通过分解相似性矩阵来得到用户和项目的低维二进制表示。然后在二进制空间计算用户和项目之间的汉明距离，距离越小表示相似性越大，用户对项目越感兴趣。由于这种二进制表示，实值向量空间的内积操作被二进制空间中的位运算所取代。因此，即使采用线性扫描，时间复杂度也能得到显著降低[3，13]。

然而，现存的基于哈希学习的推荐方法普遍存在一个问题，它们忽略了用户评分与相似性不等价问题。一般而言，用户评分系统都默认为等级评分（如豆瓣电影评分为1到5的等级），而哈希码在二进制空间的相似性区间一般为正负对称的离散区间。因此，现存的哈希推荐方法一般采用规范化的方式直接将评分映射相似性区间。这种方式是非常粗暴的，它忽略了隐藏在评分信息下用户和项目的自身特点。比如有些用户喜欢给高分，而有些用户喜欢给低分，有些项目更受欢迎，而有些项目不受欢迎[16]。

本文提出了一种改进的哈希推荐方法。它通过移除用户和项目自身的偏置将用户评分映射到正负对称的相似性区间。如图1 所示，首先，计算所有用户和项目相对于评分系统均值的偏置，在移除偏置之后，将用户评分映射到相似性区间。然后，分解相似性矩阵得到用户和项目的二进制码，在二进制空间计算用户与项目之间的相似性。最后，预测用户评分时加上对应的偏置将相似性映射到评分区间。通过这种方式，很好地缓解了用户评分与相似性不等价问题。同时，在分解相似性矩阵时，以保持相似性为目标，提出了两种结构损失来构建目标函数。实验部分，分析了三个数据集的评分分布，解释了偏置项处理的合理性，在三个真实的数据集上进行实验，对比了几个代表性方法，本文方法能实现更高的检索精度。

总结了本文的贡献如下：

（1）通过移除用户和项目的偏置，将用户评分映射到相似性区间，很好地解决了用户评分与相似性不等价的问题。

（2）以最小化相似性损失为目标，提出了两种方式来构建目标函数，并在实验中对两种方式进行了对比分析。

（3）在三个真实的数据集上的实验结果表明，与几个代表性方法对比，本文方法能实现更高的检索精度。

2 相关工作

目前，基于矩阵分解的推荐方法依然是最受欢迎的方法之一，大多数基于哈希的推荐方法都建立在矩阵分解基础上[2-3，13]。在这部分，回顾了传统的矩阵分解推荐方法和离散矩阵分解推荐方法。

2.1 实值矩阵分解

推荐系统方法包括基于内容推荐，协同过滤推荐以及两者结合的方法[17-21]。目前，协同过滤技术已经成为了主流的方法，尤其是矩阵分解的协同过滤推荐[22-25]。矩阵分解方法通过分解用户评分矩阵得到用户与项目的隐语义表示，然后在向量空间计算用户对项目的评分[16，25]。FuckSVD[26]分解用户评分矩阵，在低维的向量空间来表示用户和项目，通过向量内积来计算用户对项目的偏好。然而，完全基于向量表示来计算用户对项目的评分是不明智，因为有的用户喜欢给高评分，有的用户喜欢给低评分[16]。因此，Paterek等[27]提出了一种带偏置的矩阵分解方法BiasSVD。考虑了用户自身的评分特点以及项目受欢迎的程度。为了解决冷启动问题，Paterek 等[28]提出了一种结合内容感知和隐反馈信息的矩阵分解方法SVD++。郭宁宁等[29]人提出一种融合社交网络特征的协同过滤推荐算法，引入评分以外的信息来提高推荐的性能。虽然，矩阵分解的方法在推荐系统中已经取得了很好的表现。然而，面对日益增长数据，推荐系统的效率也面临着巨大的挑战[3，13]。

2.2 离散矩阵分解

哈希技术通过将原始数据映射为低维的二进制码表示，从而减少数据存储，加速相似性查询效率得到了广泛的关注和深入的研究[30-34]。

早期的基于哈希的矩阵分解推荐通常是一个“两阶段”的学习过程[13]。Zhou 等人[3]提出的离散协同过滤方法将二进制码的学习过程分为两个独立的阶段：实值优化和二进制量化。在实值优化阶段，通过丢弃离散约束分解矩阵得到连续解。在量化阶段，通过最小化实值的量化损失来获得二进制码。Zhang等[11]提出了一种基于余弦相似性度量的方式来分解用户评分矩阵进而得到用户和项目的二进制码。Liu等[12]提出了一种基于内容感知的矩阵分解方法，通过加入内容信息，很好地克服了冷启动问题。

图1 改进的哈希推荐方法设计流程

Zhang等[13]人指出两阶段方法由于放松二进制约束而引起的误差会导致性能差的问题，因此提出了一种离散协同过滤方法。为了解决带约束的离散化优化问题，它将原始问题转化为两个子问题。在离散化优化阶段，提出了一种离散梯度下降算法，同时采用SVD 分解方法来保持位平衡和位不相关约束来保证哈希码的有效性。Lian 等[14]在离散协同过滤基础了提出了一个结合内容感知的离散协调过滤方法。Zhang等[15]提出了一个基于深度学习的方法，采用深度信念网络来学习用户和项目的二进制表示。由于二进制码表示，实值向量空间的内积操作被二进制空间中的位运算所取代。因此，线性扫描的时间复杂度也能得到了明显降低[3，11]。

3 本文方法

假定系统中的用户数量为n，项目数量为m，用户对项目的评分构成稀疏的评分矩阵R ∈Rn×m，其中Rij表示用户ui对项目vj的评分。哈希后的用户空间为B:{b1,b2,… ,bn}∈{-1,1}r，×n哈 希 后 的 项 目 空 间 为D:{d1d,2, …,dm}∈{-1,1}r×，m其中r 是哈希码的长度。tr(⋅)表 示 矩 阵 的 迹，||⋅||F表 示 矩 阵 的Frobenius 范 数，sgn(⋅)为符号函数，输入大于等于0 时输出1，反之输出-1。1表示全为1的列向量。

3.1 模型

基于用户评分矩阵Rij，离散矩阵分解推荐方法通过分解用户评分矩阵得到用户和项目的二进制码。如果用户ui对项目vj评分越高，那么用户bi与项目dj的汉明距离越小，相似性越大。其中，bi与dj的相似性定义如下[3]：

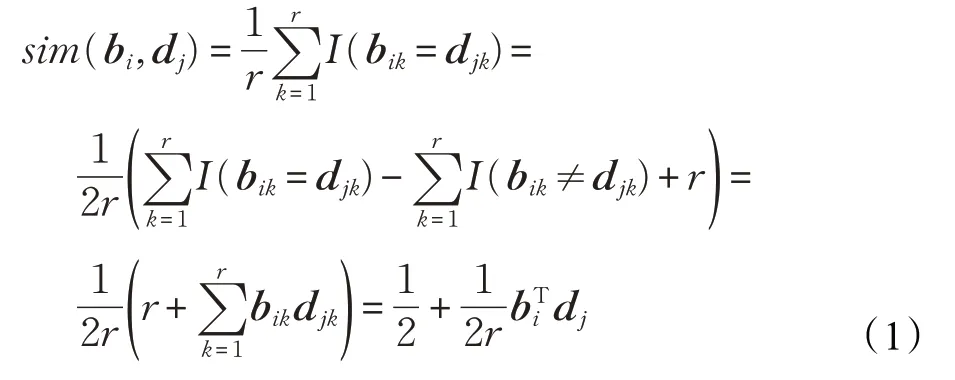
其中，I(⋅)为指示函数，如果条件成立则返回1，否则返回0。由式（1）定义可知，当用户与项目的向量内积越大，相似度越大，反之越小。另外，为了最大化哈希码的信息熵和方差，定义位平衡B1=0,D1=0和位不相关约束BBT=nIr×r,DDT=mIr×r来保证每一位哈希码的有效性。因此，现存的离散矩阵分解方法通常建立如下目标函数：

在大多数评分系统中，Rij为1～5 的等级评分，而∈{-r,-r+2,… ,r-2,r}。因此，现存的方法大多都对原始用户评分Rij∈[min s,max s]进行规范化处理Rij=2r(Rij-r)/(max s-min s)-r[13-15]。然而，这种方式忽略了隐藏在评分信息下面的用户和项目的自身特点。比如，有些用户喜欢给高分，有些用户喜欢给低分，有些项目更受欢迎，而有些项目不受欢迎[16]。直接映射处理无法挖掘潜藏在评分信息下的用户和项目的特点。因此，提出了基于偏置的方式将用户评分矩阵映射到正负对称的相似性区间。

在式（3）中，根据每个用户，项目以及评分系统的特点，将评分矩阵映射到了正负对称的相似性区间。很好地缓解了评分与相似性不等价问题，同时挖掘了用户与项目自身的特性。而然，的内积值与哈希码的长度有关，因此，只需要将相似性Sij归一化到[-r,r]。最终，目标函数如下：

其中，Sij∈[-r,r]为用户ui与项目vj的相似性。

问题4 本质上是一个带约束的离散化优化问题，直接优化是一个NP 难问题[35-36]。因此分别定义了两个 约 束 空 间 Φ={X ∈Rr×n|X1=0,XXT=nIr×r} 和Ω={Y ∈Rr×n|Y1=0,YYT=mIr×r}。通过放松哈希码的位平衡和位不相关约束得到一般化的目标函数：

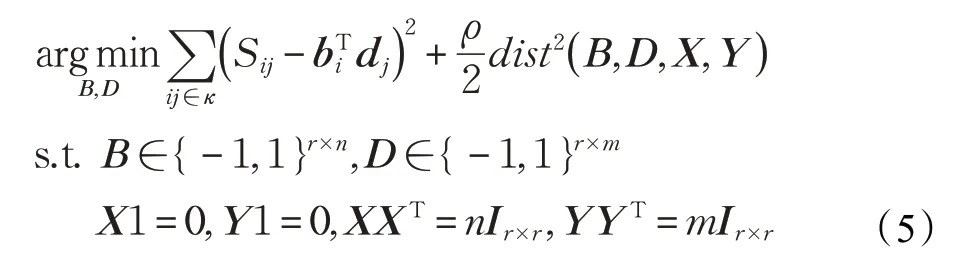
其中，dist( )B,D,X,Y 表示{B,D}与{X,Y}之间的距离。本文提出了两种度量方式如下：

值损失度量：分别衡量两个矩阵中所有元素对应之间的误差：

相似性损失度量：衡量两个矩阵乘积之后相似性矩阵中所有元素对应之间误差：

由tr(BBT)=tr(XXT)=nr、tr(DDT)=tr(YYT)=mr，可得，式（6）对应的值损失目标函数：

类似的，式（7）对应的相似性损失目标函数：

其中，式（8）和式（9）中的ρ ≥0,ρ1≥0,ρ2≥0 是调节参数。值得注意的是，可以通过设置一个很大的调节参数来强制dist(B,D,X,Y)→0。

3.2 学习

针对不同损失度量得到的目标函数式（8）和式（9），学习算法的过程类似，这里详细介绍了相似性损失目标函数的学习过程。对于式（9），采用交替求解如下四个子问题：

B-问题：在这个问题中，固定D,X,Y，B-问题转化为最小化目标函数：

其中，κi表示用户ui的所有评分项目集合。

哈希码的求解过程是一个离散优化问题，早期的方法放松哈希码的离散约束来解决一个近似的优化问题，但这导致难以获得高质量的哈希码[35]。因此，Liu 等人[35]提出一种离散优化方法，同之前的工作一致[13，15]，采用离散坐标下降优化算法来更新每一位哈希码。用bik表示bi的第k 位哈希码，bikˉ表示除第k 位剩下的哈希码，在固定bikˉ不变的时候，bik的更新规则如下：

D-问题：在这个问题中，固定B,X,Y，D-问题转化为最小化目标函数：

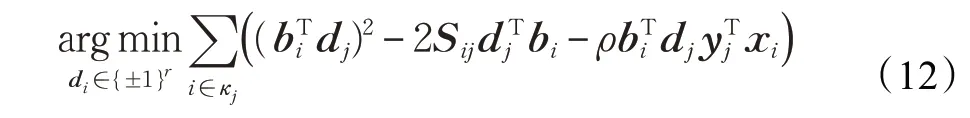
其中，κj表示项目vj的所有评分用户集合。同B-问题类似，D的更新规则如下：

X-问题：在这个问题中，固定B,D,Y，关于X 的目标函数如下：

为了保证X 的位平衡和位不相关约束，采用SVD分解求解式（14），记P=( BTDYT)T，X的更新规则如下：

其中，Ub和Vb分别是矩阵的左右奇异值是对应0 奇异值的特征向量基于[Vb1]斯密特正交化获得[13]。

Y-问题：在这个问题中，固定B,D,X，关于Y 的目标函数如下：

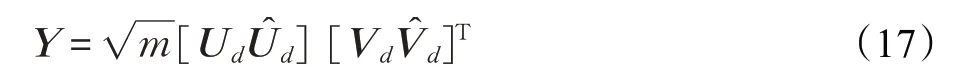
4 算法分析

算法1 总结了整个优化过程，下面分析算法的复杂度和收敛性。

算法1

输入：评分矩阵{Rij|i,j ∈κ}，哈希码长度r，调节参数ρ

输出：用户哈希码B ∈{±1}r×n，项目哈希码D ∈{±1}r×m，偏置项

p=max(Sij),q=min(Sij)

Sij=(Sij-p)/(p-q)*2r+r

初始化：随机初始化X,Y，B=sgn(X),D=sgn(Y)循环

直到收敛

4.1 复杂度

分析了算法的时间和空间复杂度。对于空间复杂度，算 法1 需 要O(|κ|)来 存 储 稀 疏 的 评 分 矩 阵，需 要O(r.max(m,n))来存储用户和项目的哈希码，其中r 是哈希码的长度。另外，需要少量的空间O(m+n)来存储用户和项目的偏置信息。因此，整个算法的空间复杂度是线性的。

算法1 的时间复杂度包括预处理和四个子问题。预处理过程需O(κ)来完成评分到相似性的映射。对于B-问题，需要O(r2|κi|Ts)来计算用户的哈希码，其中Ts是更新一位哈希码的时间。类似的D-问题需要O(r2|κj|Ts)来计算项目的哈希码。对于X-问题需要O(r2(m+n))来进行SVD 分解和斯密特正交化，类似的Y-问题也需要O(r2(m+n))。假设算法需要迭代T 步收敛，那么整个算法的时间复杂度为O(Tr2((|κi|+|κj|)Ts+m+n))。因此，算法的样本时间复杂度趋于线性。

现有的方法的核心过程大多是分解相似性矩阵，本文的方法相比于DCF多了一个预处理过程-评分到相似性的映射，该过程的复杂度与用户评分数量是线性关系。由于BCCF、PPH 直接放松了哈希码的离散约束来解决一个近似的优化问题，因此它们不涉及X-问题和Y-问题。相比而言，BCCF、PPH 多了一个连续值到哈希码的量化过程。总的来说，算法1 的时间复杂度同三个代表性方法相当。

4.2 收敛曲线

如图2 所示，给出了算法在Movielens-10M 数据集上目标函数与哈希码长度比值的收敛曲线。从图2 中可以看出算法在20 次迭代左右收敛，且收敛效果与哈希码的长度正相关。算法的收敛速度非常快，尤其是前面几次迭代。算法收敛性的理论分析与EM 算法的收敛性证明类似，详细的收敛性分析参见文献[13]。

图2 目标函数收敛曲线

5 实验

实验中，在三个标准数据集上，对比了三个有代表性的哈希推荐方法BCCF、PPH、DCF。其中BCCF 和PPH 为两阶段哈希方法，PPH 采用余弦相似性度量，DCF 直接离散优化获得哈希码。所有的实验运行在16 Intel Xeon CPU和64 GB RAM平台。

5.1 数据集

使用如下三个标准数据集：

MovieLens-10M：这个数据集包括71 567 个用户，10 681 部电影和107个评分信息。所有的评分在0.5～5之间，以0.5为间隔。

Douban：这个数据集包括129 490个用户，58 541部电影和16 830 839 个评分信息。所有得评分在1～5 之间，以1为间隔。

Epinions：这个数据集来自于40 163个用户对139 738部电影的664 824 个评分。所有的评分在1～5 之间，以1为间隔。

为了验证本文的方法适合不同评分密度的数据，选择了三个不同评分密度的数据集。同之前的工作一样[14-15]，过滤了评分信息不足50 个的用户，使得每个用户都有可观察的评分信息用于训练和测试。对于每个用户，选择80%的评分信息作为训练数据，剩下的20%作为测试数据。总结了过滤处理后的数据集如表1。实验中，对数据集进行了5 次同样比例的随机划分，并取5次实验结果的均值来评估所有的方法。

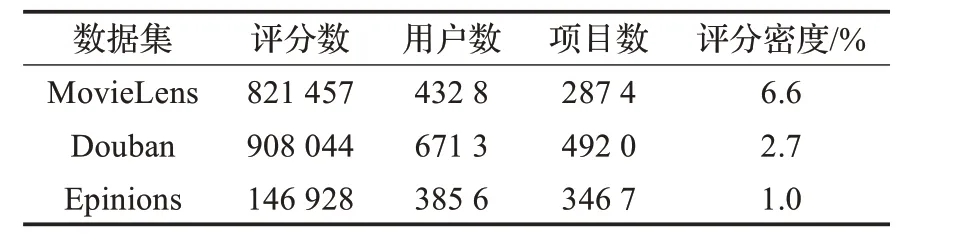
表1 过滤后的数据集

5.2 评分分布

为了分析移除偏置的合理性，对三个数据集的评分分布进行了统计分析。如图3 所示，发现三个数据集的用户评分以3 到4 分所占的比例最多，两端的比例相对较少评分分布大致服从正态分布。这表示，大多数用户的评分具有一定的习惯，即存在一个评分平衡点，同时所有的评分是在这个平衡点上下浮动。因此，一个基本的假设就是将用户均值以及项目均值相互作用看作是平衡点，偏离平衡点偏差则通过哈希码之间的相似性来拟合。

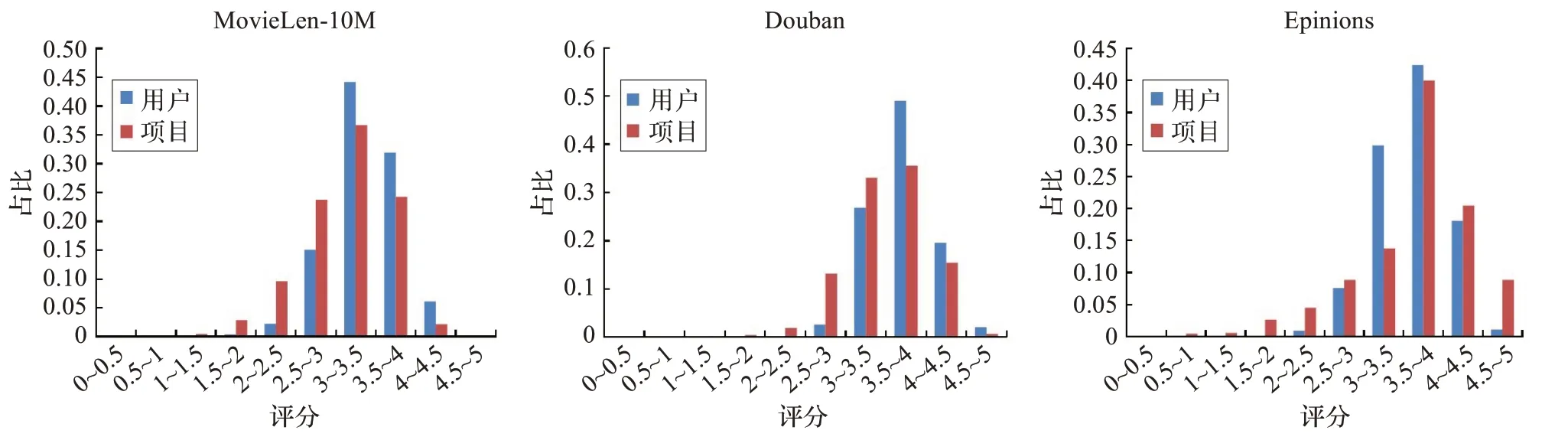
图3 三个数据集的用户评分数据分布

5.3 评价指标

采用了如下三个常用的评价指标：

NDCG：折扣累计损失（DCG）是广泛用于评价排序质量的指标。NDCG 则是对折扣累计损失归一化的结果。NDCG 关注于算法获得的哈希码对保持用户对项目的偏好排序的结果。NDCG计算如下：

其中，K 为排序靠前的K 个项目，ri是算法预测第i个偏好的项目的得分，而rj则是由用户评分信息得到的第j个偏好的项目的得分。因为排序越靠前的项目得分权重越大，而且rj是实际用户评分排序后的结果，所以NDCG的分母一定大于分子，即NDCG在0到1之间，越大说明保持用户偏好排序的效果越好。

RMSE：平方根损失误差是用来评价算法预测的评分与用户的实际评分的偏差，不保持评分之间的排序关系。RMSE计算如下：

其中，κ 是所有可观察的评分集合，yk为预测评分，ŷk为真实评分。

Precision、Recall、F1：精度、召回率、F1 值是常用的分类指标。在这里，用于评价算法在预测用户对项目是否喜欢的二类问题上。它们的计算公式如下：

对于每一个用户，设置预测评分5 分以上的项目构成集合，实际评分为5分的项目构成集合。

5.4 实验结果

5.4.1 对比实验

同以往的工作一样[3，13-15]，使用NDCG 和F1指标，对比了本文的方法同其他三个代表性的方法。

在表2 中，报告了不同方法在三个数据集上的NDCG@10 精度，可以看出本文的方法有一定的优势，尤其是较短哈希码长度下，相对于DCF 方法大约有1%～3%的提升。而且，OUR-S 在短哈希码下的表现更显著。在表3 中，展示了不同方法的F1 值，可以看出本文方法在大多数情况下优于其他方法，在8 bit 哈希码下，本文的方法表现优越，相对于DCF 方法大约有3%～5%的提升。另外，在图4 中展示了不同方法在不同哈希码长度下的NDCG@K 随K 的变化曲线，图5 中展示了召回率-精度变化曲线，从图中可以看出，本文的方法保持一致的优势，尤其是在Douban数据集上。

5.4.2 相似性损失与值损失区别

对于两种不同损失度量方式，大多数情况下相似性损失度量OUR-S 优于值损失度量OUR-V。如图6 所示，在NDCG@5 指标下相似性损失度量依然优于值损失度量，而且在短哈希码下这种优势较为显著。这表示相似性损失度量可以用较短的哈希码就能获得较优的结果。为了探究其中的原因，分析了两种度量的RMSE指标。如图7 所示，相似性损失度量相比于值损失度量，在预测评分上更准确，这说明相似性损失度量能更好地拟合用户评分，保持用户与项目之间的相似性。

6 总结

本文发现现存的大多数哈希推荐方法在处理用户评分信息与相似性关系上过于粗暴，没有挖掘评分信息下潜在的用户和项目的特点。因此，提出了用一个偏置项来保留这种特点，通过去偏置将用户评分映射到相似性区间，很好地缓解了用户评分与相似性不等价的问题。在构建目标函数时，提出了两种度量方式来构建目标函数，并在实验中分析了两种方式的区别，相似性损失度量优于值损失度量，尤其是在短哈希码下。然而，本文没有考虑推荐系统中的冷启动问题[28，37]，没有引入用户评分以外的信息，探究评分以外的信息对算法性能的影响是一个值得思考的问题，也是下一步要研究的工作。

表2 不同方法在三个数据集上的NDCG@10值%

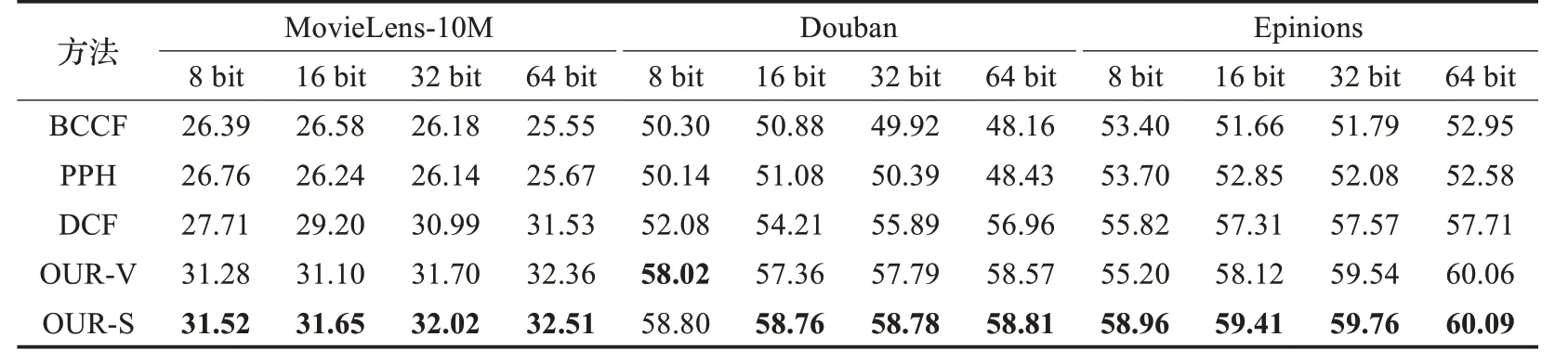
表3 不同方法在三个数据集上的F-measure值%

图4 不同方法在不同哈希码长度下的NDCG@K值(K=2,4,6,8,10)

图5 不同方法在不同哈希码长度下的召回率-精度曲线

图6 两种度量方式在不同哈希码长度下的NDCG@5值

图7 两种度量方式在不同哈希码长度下的RMSE值