可能性聚类假设的半监督分类方法

但雨芳，陶剑文，徐浩特

1.宁波职业技术学院 电子信息工程学院，浙江 宁波315800

2.宁波大学 信息科学与工程学院，浙江 宁波315211

3.江西理工大学 信息工程学院，江西 赣州341000

1 引言

有效的机器学习需要大量带标签的数据，在实际应用中，充足的带标签数据通常难以获取，虽然手工标注数据可以一定程度上弥补带标签数据的缺乏，但是这个过程较费时费力。为此，半监督学习（Semi-Supervised Learning，SSL）[1-11]方法得以提出，其从少量标记的数据和大量未标记的数据中学习得到模型，解决了带标签数据不充足而导致有监督学习得到的模型泛化能力不强，以及由无监督学习得到的模型不精确等问题。吴明胜等人[12]提出一种基于协同训练与差分进化的改进ELM算法的半监督分类方法来改善神经网络的输入层参数的随机初始值对分类的影响，祖宝开等人[13]提出了基于分块低秩图的大规模遥感图像半监督分类应用来有效提升分类性能，因基于图的半监督学习方法（Graph based SSL，GSSL）[14-17]凭借其直观性和良好的学习性能而得到广泛的研究。GSSL具有两种不同类型的推理方式，即转导式推理（Transductive inference）[5，7，18-19]和归纳式推理（Inductive inference）[6，20-21]，转导式推理在假设学习过程中无标签的数据正好是测试数据，对于新来的样例（out-of-sample）并没有很好的预测效果；比如，方法LGC[5]、GFHF[7]、LNP[18]和ACA-S3VM[19]等；而归纳式学习在假设学习过程中将所有数据归到一起找出其共性，进而得到一个模型，且测试数据不在训练数据内；流行正则化框架（Manifold Regularization，MR）[20]就是一个非常常见的归纳式GSSL 推理模型，比如：方法GLSSVM[6]、FME/U[21]等；其中，Nie 等人[21]所提方法FME/U对MR框架进行了一般化归纳。通常情况下，采用GSSL推理方式，都需要采用某些假设。其中，最常见的假设之一是聚类假设：“类似的实例应该享有相同的标签”[2-3，9-11，22]。而该假设还具有一个隐含的前提，即每个实例都应该明确地属于某一个类别。然而，在某些实际分类应用中，很难严格符合这一前提。比如，在图像分割中，边界像素可以属于任一类，在电影类型分类中，中国文学家莫言的长篇小说《红高梁》改编成电影，该电影可以是战争类型，也可以是文艺类型等等。

为了解决聚类假设的硬划分问题，Wang 等人[17]提出了一种基于新聚类假设的半监督分类（即SSCCM）方法，是聚类假设的一种软划分方法，其旨在“类似实例应该共享相同的标签隶属度”，每个实例都可以隶属于多个类标签，且有对应的隶属度值，很好地利用了模糊聚类假设[23]。然而，其约束条件使得每个实例对于不同标签的隶属度之和总为1，可能会导致某些噪声的标签隶属度与某些正常数据的标签隶属度一样，甚至对于某一个或多个类，噪声的标签隶属度值可能比正常数据的更大，即相关性更大，这样就会因为噪声问题导致错误分类。

针对SSCCM 方法存在的问题，本文提出一种基于可能性聚类假设的半监督分类（即SSPCA）方法，该方法的主要思路是：首先，以每个数据点与其局部加权均值（Local Weighted Mean，LWM）[24-26]的标签隶属度相似，然后，通过决策函数和隶属度函数各自得到的分类预测结果进行相互验证，以此来提高分类的可靠性，最后加入了一个关于模糊熵的正则项，通过增大样本判别信息量来得到一个泛化能力更强的隶属度函数，从而克服噪声和异常数据对分类结果的干扰，更进一步提高该分类方法的鲁棒性。本文的主要贡献在于：（1）提出了一种基于可能性聚类的半监督分类方法；（2）该方法引入了一个关于模糊熵的正则化项，得到一个具有更强泛化能力的标签隶属度函数，使其克服噪声和异常数据的影响来提高该方法的鲁棒性；（3）最后在实际数据集上做了大量的实验，证明了该方法的鲁棒有效性和分类可靠性。

2 SSPCA

2.1 问题描述

当前，在实际分类应用中基于半监督的聚类方法存在一些实例难以将其明确分配给单一类，例如那些边界实例，由于传统的硬聚类假设隐含地约束每个实例具有清晰的标签分配，不能充分反映实际数据的分布情况，还有可能违反这些边界实例的分布。因此，该假设应用于半监督分类时，对那些边界实例的预测效果会比较差，尤其是当一些带标签的实例位于边界附近时，将会进一步“误导”分类。Wang 等人[17]提出聚类假设的软划分方法在一定程度上改善了传统聚类假设的硬划分方法，其每个实例都将拥有关于不同类的标签隶属度值，而不是只属于某一个类，这样，可以减小那些边界实例的“误导”分类影响。例如，图1 中有一个无标签的实例x2，按照SSCCM 方法可知，x2属于Class1 和Class2的隶属度值各为0.5。图1 中，在类簇Class1 和Class2 中，带问号的人造数据○和☆是不带标签的数据，其他人造数据是带标签数据，虚线是两类簇的正中间分割线。但是，直观上看，x1可以看成是边界点或者是离群点，x2肯定比x1更像是属于Class1 和Class2 的实例，然而，继续按照SSCCM 方法来计算隶属度，距离哪个类最近，其隶属度值就越大，反之越小，因此，实例x1属于Class1 和Class2 的隶属度值分别是0.6 和0.4，x1属于Class1 的隶属度值比x2要大，导致x1比x2更加像是属于Class1。这样的结果主要是由于SSCCM 中约束单个实例的所拥有的不同标签的隶属度之和总为1，哪怕是x1这样的边界点或者离群点都不例外。

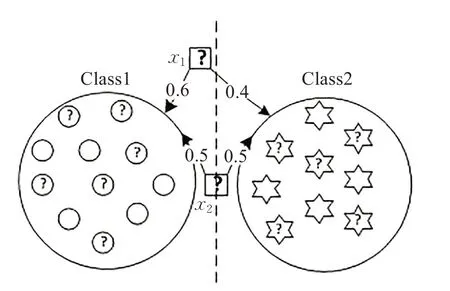
图1 问题描述

为了克服离群点数据给分类带来的负面影响，本文将提出一个基于可能性聚类假设的半监督分类（即SSPCA）方法。

2.2 SSPCA方法

为了使聚类假设的分类方法具备更加好的分类可靠性和鲁棒性，SSPCA 方法实现如下三个目标：（1）任意一个实例应该与其对应的局部加权均值点具有相似的标签隶属度；（2）决策函数与隶属度函数对某一测试实例的分类结果可以进行相互验证且具有收敛性；（3）克服噪声和异常数据其带来的分类影响。本文所提分类方法将通过欧氏距离求得每个数据点的局部加权均值，然后通过平方损失函数迭代求得所需要的决策函数以及标签隶属度函数，并利用加入的模糊熵正则项来克服噪声和异常数据的影响，提高该方法的鲁棒性，最终构建一个优化后的双重验证分类器模型：决策函数f(x)和隶属度函数w(x)。

设给定数据集X={x1,x2,…,xi,xi+1,…,xn}，其中为l 个带标签的数据集，其相应的l 个标签集Yl={y1,y2,…,yl}T∈ℝl×M，n为数据集的总数量，且l ≪n，为(n-l)个无标签的数据集，其中，每个xi∈ℝd为第i个实例，有d 个维度。每个实例xi的LWM（即̂）的定义为：

其中，Ne(xi)定义为xi的k 个最近邻实例的集合，xj∈Ne(xi)。G=(X,W)定 义 为 无 向 权 值 图，其 中，W ∈ℝn×n为权重，Wji=Wij≥0。其中元素值的计算方法为：

其中，γ 是控制高斯核函数的局部作用范围，γ 越大，局部作用范围（即，宽度）越小，反之，其局部作用范围越大，在γ固定的情况下，Wij值的变化是随着xi和xj间的距离增加而单调变小的，由此将聚类问题转化为图划分问题。和分别是l 个带标签数据和(n-l)个无标签实例的LWM。是M 个类的编码表示，如果xi属于第m 类，那么yi=cm，数据标签和类别编码都是按照属于M 个类中的一个类别来进行编码的，即数据标签和类别的编码都是维度为M 的向量，所以，SSPCA 能直接应用到多类分类任务中去。设yi∈ℝ1×M和cm∈ℝ1×M，如果xi属于第m 类，那么yi的第m 个元素就指定为1，即yim=1,m=1,2,…,M，yi的其他元 素 为 0，即 yio=0,o=1,2,…,M，且；且cm=1,m=1,2,…,M 的第m 个元素设置为1，即cmm，cm的其他元素为0，即cmo=0,o=1,2,…,M，且。除了决策函数f(x)，该方法还需要定义一个隶属度函数w(x)，对任意一个实例xi都会有w(xi)∈ℝM，且wm(xi)为xi属于第m 类的隶属度值。最后，通过本文改进的分类方法，依据局部学习原理来约束每个实例与其相应的LWM 共享相同的隶属度向量[25-26]，SSPCA 的优化问题可描述为：

对于带标签的实例，标签隶属度函数公式可以描述为：

其中，Xm为带标签实例集中属于第m 类标签的实例子集。由此可知，公式（2）可改写成公式（4）。

通过SSPCA 方法，使得每个实例都有关于所有标签的隶属度值，并且，每个实例和它对应的LWM都共享相同的隶属度值。

需要说明的是，在公式（2）中，采用的是平方损失函数，采用其他分类损失函数也可以用在开发基于可能性聚类假设的不同半监督分类方法中。本文的公式（2）与SSCCM[17]中公式（3）对比，放松了标签隶属度加权和为1 的约束条件，并加入了模糊熵正则项来克服噪声和异常数据对分类的影响，使得模型更具有鲁棒性。

3 优化

SSPCA 的优化问题是一个关于(f,w)非凸的问题，本文是采取交替迭代优化的策略来分别实现决策函数f(x)和标签隶属度函数w(x)的优化求解，并且每一步迭代都有一个闭环解。

先固定w(x)求解f(x)，由于公式（4）中的第六项没有关于f(x)的计算，所以SSPCA 的优化求解可以描述为公式（5）：

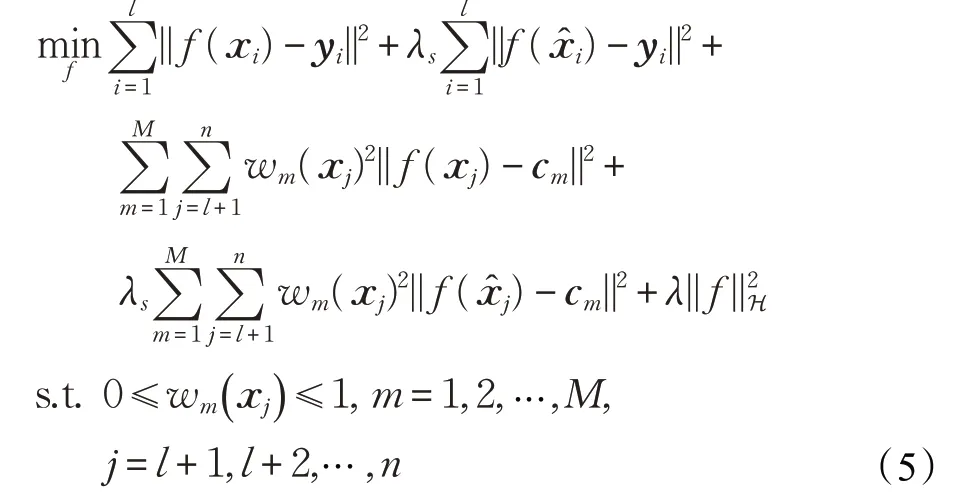
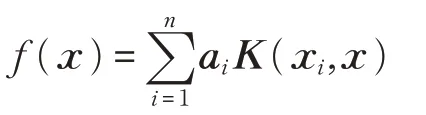
其中

令∂F1/∂α=0，求解α，其描述为：

依据推导求得α的解，定理1得证。

再固定f(x)求解w(x)，那么SSPCA 的优化问题可以描述为公式（10）。

定理2目标函数（即，公式（10））的原始优化问题的最优解为：

证明令∂F2/∂wm(xj)=0求解wm(xj)，可得：

得出wm(xj)的解为：

因此，任意实例x 的标签隶属度值都可以由公式（11）推导得到，定理2成立。

4 算法描述

SSPCA的优化采用的是交替迭代策略，SSPCA属于直接寻求大边界分离器的半监督大边界方法的范畴。实际上，迭代式学习过程常用于各种半监督学习方法中。无标签实例的隶属度初始值可以通过几种策略获得，例如，随机化策略，或者某些模糊聚类技术（如FCM），或者简单地置全零，在这种情况下，SSPCA 实际上是从带标签的数据上开始学习，来初始化决策函数f(x)。当|F(αm,wm(x))-F(αm-1,wm-1(x))|＜εF(αm-1,wm-1(x))时，迭代终止，其中F(αm,wm(x))表示第m 次迭代时目标函数的值，ε是预定义的阈值。

SSPCA算法描述

输入：带标签的数据集Xl和其对应的标签集Yl，无标签的数据集Xu，正则项参数λ,λs,C，迭代终止的阈值ε，以及最大迭代次数T。

输出：决策函数f(x)，标签隶属度函数w(x)。

处理过程：

1.初始化无标签数据集的标签隶属度值；

2.通过公式（6）获得α的初始值；

3.通过公式（11）获得w(x)的初始值；

4.计算目标函数的F(α0,w0(x))值；

5.依次以m=1,2,...,T 重复以下步骤：

{

5.1 通过公式（6）更新α的值；

5.2 通过公式（11）更新w(x)的值；

5.3 更新目标函数的F(αm,wm(x))值；

5.4 如果|F(αm,wm(x))-F(αm-1,wm-1(x))|＜εF(αm-1,wm-1(x))，则终止重复计算，并返回f(x)和w(x)；

5.5 否则，回到5.1 继续计算，直到5.4 的判断条件满足为止。

}

5 讨论

5.1 SSPCA的分类可靠性

为了更进一步增强分类的可靠性，SSPCA 通过决策函数和标签隶属度函数相互鉴定彼此的预测分类结果，使其分类结果更具可靠性。由此可得出定理3。

定理3SSPCA 利用决策函数和标签隶属度函数来进行预测，并且它们各自的预测结果通常是一致的（实际一致或间接一致）。若两个预测结果不一致，则相应的实例可能位于决策边界附近，并且这些预测可能是不可靠的。

证明数据可以由定理1 得出的决策函数或者是由定理2 得出的标签隶属度函数来进行分类预测，在∀j=1,2, …,M;j ≠m 的情况下，如果用f(x)来 预测，fm(x)＞fj(x，)那 么x ∈Xm；如 果 用w(x)来 预 测，wm(x)＞wj(x)，同样可得x ∈Xm的结果。在λs固定不变的情况下，fm(x)+λsfm(x)＞fj(x)+λ fs(jx)也能得到上面一致的预测结果；当λs=0，f(x)和w(x)的预测结果总是一致的。当λs0，通过f(x)使得x 和x̂享相同的标签分配时，即，f(x)和w(x)的 预 测 结 果 也 是 一 致 的；若fj(x )-fm则f(x)和w(x)预测结果也是一致的。如果x 位于决策边界附近，x 和x̂的预测差异是很明显的，有可能x̂直接位于与x 相异的类别中，那么，对x 的这种预测是不可靠的。可以总结出三种实例：（1）实际一致性实例，通过f(x)得到实例x 和̂享有相同的标签分配，使得f(x)和w(x)对x的预测结果一致；（2）间接一致性实例，x 不是实际一致性实例，但是使得f(x)和w(x)对x 的预测结果仍然一致；（3）不一致性实例，f(x) w和 (x)对x 的预测结果不一致。从而定理得证。

实际上，只需要一个函数来预测新实例，如果期望得到某些实例属于每个类的隶属度，则首选标签隶属度函数。用这两种函数来预测实例，则是利用它们的预测不一致性来检测那些难以分类的边界实例，并对它们进行特殊处理，例如手动标记，以提高分类可靠性.这两个函数的预测可以相互验证，并且可以通过检查它们的一致性来增强半监督分类的可靠性。

5.2 SSPCA算法的收敛性

为了证明算法1的收敛性，可得出定理4：

定理4在上述算法SSPCA 中获得的序列{F(αm,wm),m=1,2,… ,T}是收敛的。

证明由于目标函数F(α,w)在(α,w)上是一个双凸函数[29]。固定不变w(x)，且目标函数在α 上是凸函数，因此可以通过公式（6）最小化F(α,wm)或等效地优化公 式（5）来 获 得 最 优 α*。αm+1=α*，得 出 ：F(αm+1,wm)=F(α*,wm)≤F(αm,wm)。此时，固定αm+1，且目标函数在w上是凸函数，因此，可以通过公式（11）最小化F(αm+1,wm)或等效地优化公式（10）来获得最优w*。wm+1=w*，得 出：F(αm+1,wm+1)=F(αm+1,w*)≤F(αm+1,wm)，可推理得出：F(αm+1,wm+1)≤F(αm+1,wm)≤F(αm,wm),∀m ∈N，{F(αm,wm)}是单调减小的。此外，由于目标函数是非负的，因此具有较低的界限。从而定理成立。

5.3 SSPCA的泛化误差界

在统计学习理论中，VC 维（Vapnik Chervonenkis dimension）[30]提供了一个可分析机器学习的泛化误差界方法[31]。因此，本文采用VC 维方法对SSPCA 进行泛化误差界的分析。

定理5（SSPCA 泛化误差界）设H 为再生核希尔伯特空间（RKHS），核SSPCA 方法的学习函数fΦ∈H 的泛化误差界在概率1-δ(0 ＜δ ＜1)下满足下式：

由定理5 分析可得，该方法的泛化误差可以通过隶属度函数wm(x)来调节控制，使其具有取得更优泛化性能的可能性。

6 实验分析

该部分将在真实数据集（UCI[32]、Benchmark[2]）上进行SSPCA 方法与最新的半监督分类方法的比较，以及SSPCA 方法与hard SSPCA 方法的比较。在UCI 和benchmark 数据集上进行SSPCA 与最新的半监督分类方法和SSPCA 方法与hard SSPCA 方法的分类结果比较。研究如下几个问题：

（1）SSPCA 与最新的半监督分类方法如何进行比较的。

（2）SSPCA与hard SSPCA如何进行比较的。

（3）正则化参数λs是如何影响SSPCA 内在一致性的。

6.1 比较的方法

该实验部分将本文的SSPCA 方法与LapSVM[20]、LapRLS[20]、TSVM[33]、meanS3VM[34]，以及SSCCM[17]5 个最新的半监督分类方法进行比较。

LapSVM：拉普拉斯支持向量机。该方法采用流型假设进行半监督分类，其使用的损失函数是铰链损失（hinge loss）函数，按照拉普拉斯图平滑地在整个数据分布上来寻找一个最大面的决策函数。

LapRLS：拉普拉斯正则化最小平方。方法采用的也是流型假设进行半监督分类，但是，其使用的损失函数是最小平方损失函数。

TSVM：转导式支持向量机。该方法采用的是聚类假设，目的是为了在带标记和未标记的数据上寻找一个分界面，以便通过低密度区域引导出分类边界。

MeanS3VM：基于无标签数据的标签均值的一种半监督SVM。也采用聚类假设，实际上包含两种实现方法[28]，即基于交替最优化的meanS3VM-iter 方法和基于多重内核学习的meanS3VM-mkl方法。

SSCCM：基于修改聚类假设的一种新的半监督分类方法。也采用的是聚类假设，其目的是为了在带标签和无标签的数据上寻找一个隶属度函数和一个决策函数，使得相似的实例应该共享相似的标签隶属度，且一个实例可以隶属于多个类。

此外，本文还将SSPCA 方法与hard-SSPCA 方法进行比较，hard-SSPCA 分类方法只是采用了聚类假设，它指定每个实例都明确属于一个类标签，而没有多类标签的概念，可描述为：

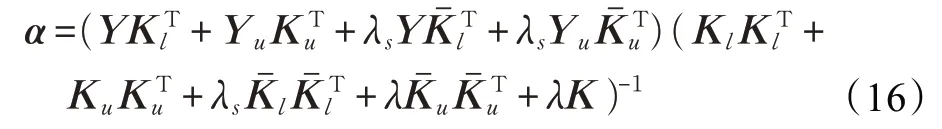
6.2 实验设置

该部分将分别细化实验参数设置。对于UCI 数据集，数据集的设置将会参照文献[17，34-35]。其每个数据集都是随机分成一个训练集和一个测试集，其中，训练集仅包含10 个带标签的实例，其他的都是无标签实例。这一处理过程通过采用线性核，先重复20 次的分类学习，然后得到一个平均测试性能的结果。这些需要进行比较的最新方法（SSCCM 方法除外）上，将正则化参数C1和C2分别固定为1 和0.1，采取1 对多策略来解决多分类问题。

对于Benchmark 数据集，实验参数设置是参照文献[2，34]进行设置的，每个数据集有两个设置，一是10 个带标签实例，二是100 个其他实例，此外，每个数据集的每次设置都有12 个关于有标签数据的子集以及得到在无标签数据上的平均测试性能结果。那些被比较的方法（SSCCM除外）中，正则化参数C1和C2分别设置为100和0.1，在SSCCM、SSPCA 和Hard SSPCA 方法中，参数λ、λs、m和ε分别设置为1、0.1、5 和10-3。需要使用线性核和RBF 核，当标记10 个实例时，RBF 内核中的宽度参数设置为实例之间的平均距离，并在具有100 个带标签实例时，通过对标签数据进行10 倍交叉验证，最后选择在每个数据集上关于这两个内核之间更好的结果。方法的结果取自文献[2，17，34]（每个数据集在每次运行时，带标签实例和无标签实例的划分参考文献[2，17，34]）。

6.3 实验结果分析

特别说明，在以下实验数据表格中，每列中的粗体值表示验证方法达到的最佳测试准确度或平均性能结果。每行（最后一行除外）对应于每种方法在各个数据集上的测试准确度，最后一列显示了在所有数据集上各个方法的平均测试性能，其中，在表1～表3中，最后一行给出了各个数据集上关于SSPCA 的一致率。表1～表3结果，可得出如下几点结论：

表1 各方法在9个二类UCI数据集上的性能比较

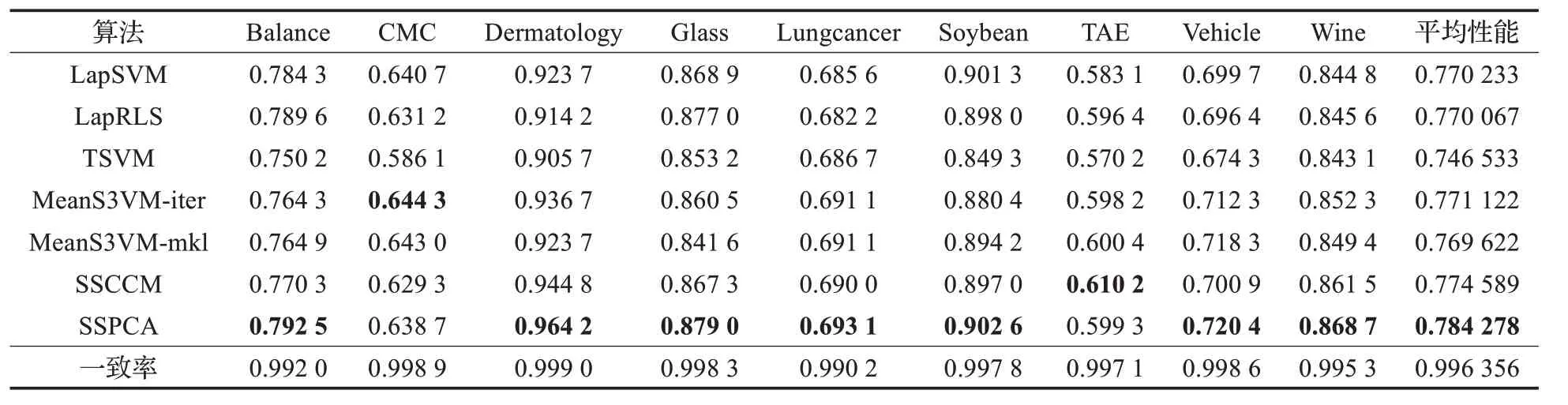
表2 各方法在9个多类UCI数据集上的性能比较

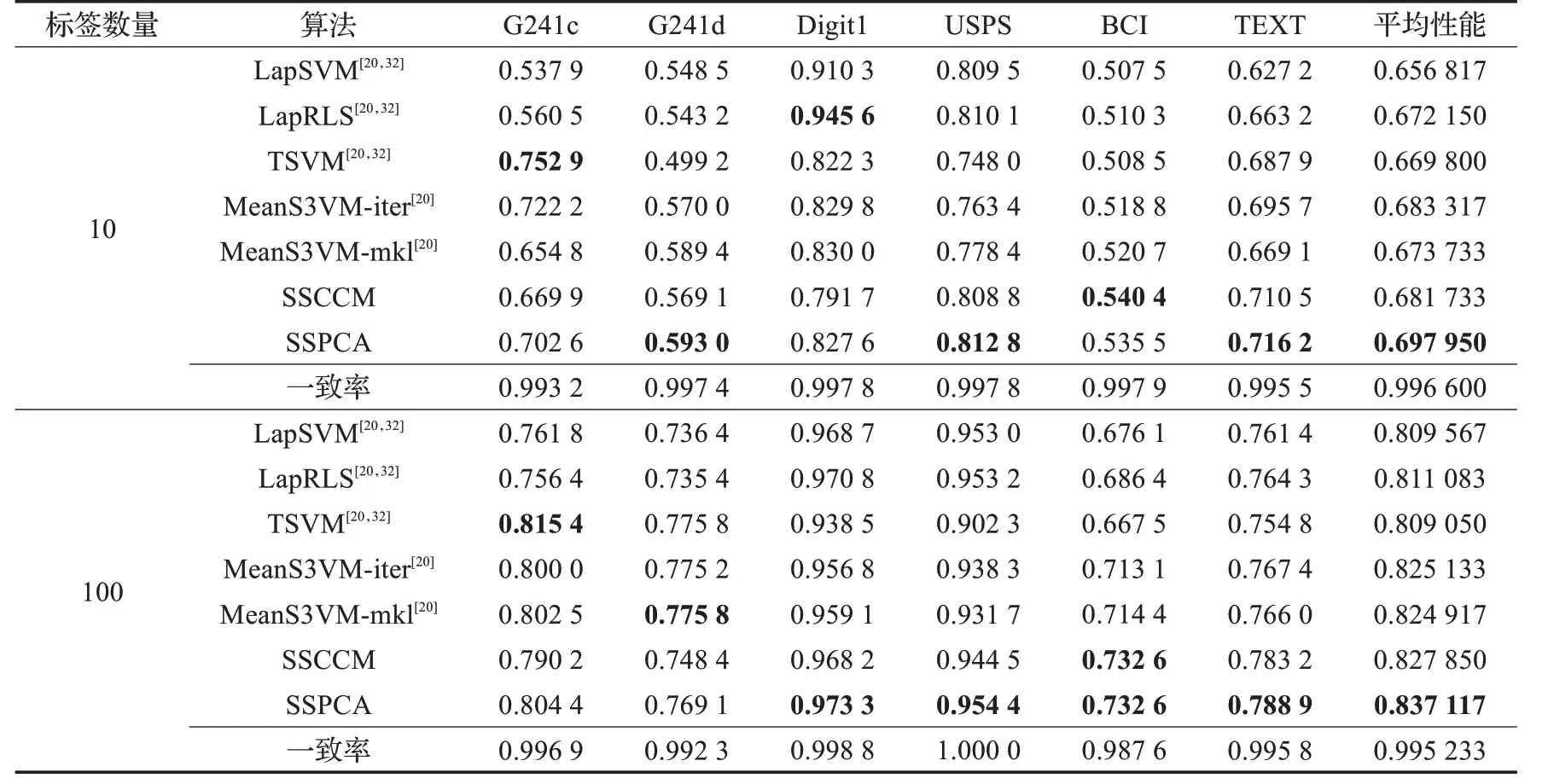
表3 各方法在6个基准数据集上的性能比较

（1）SSPCA 与那5 个最新方法的实验比较是在9 个二分类的UCI 数据集上进行的，实验结果如表1 所示，所提方法的平均性能是最好的。此外，其一致率均接近1；尽管在Heart 数据集上得到的一致率最差，其值也高达0.993 3。值得说明的是，其中方法LapSVM和LapRLS在4 个数据集上的测试性能都达到了最佳，而这两种方法是针对流型结构的数据进行处理的，因此，其可能的原因是这4 个数据集上的数据均具有流型化结构。另外，MeanS3VM-iter 和MeanS3VM 均在Sat16 数据集上的测试性能最优，其可能的原因是该数据集的数据结构复杂，MeanS3VM 主要也是针对结构复杂的无标签数据在训练期间起到负面效果时进行处理。然而，在个别数据集上其他方法的测试性能略优的同时，所提方法的性能也是紧随其后的，且所提方法在大多数数据集上均具有最佳的测试性能。这表明增加模糊熵的聚类假设对于半监督分类中克服噪声的影响是有很明显效果的。

（2）SSPCA 与那5 个最新方法在9 种多类UCI 数据集上进行比较的结果显示在表2中，其结构与表1相同。从表2 中可看出，虽然，MeanS3VM-iter 方法在CMC 数据集上测试性能最佳，然而，SSPCA 方法的测试性能与该方法也是非常接近；另外，SSCCM 方法在数据集TAE上的性能略优于所提方法，其可能的原因是该数据集上的数据分布本身比较有规则，噪声或者异常数据少或是没有，而无法体现所提方法的优势。然而，可以很明显看出SSPCA 在7 个数据集上的测试性能均优于其他方法，并在平均测试性能上达到了最优。同样，SSPCA 的一致率均接近1，即使在肺癌数据集上得到的一致率最差，其值也高达0.990 2。最后，由于所提方法是针对多类分类的，相较于在二分类的UCI 数据集上的测试结果，该方法在多分类的UCI数据集上也具有明显优势。

（3）SSPCA 与那5 个最新方法在6 个基准数据集上进行比较的结果见表3，其中，上半部分和下半部分分别对应于有10 和100 个带标签实例的实验结果。从表3上下两个部分可以明显看出，方法TSVM 在表中的上下两个部分的G241c数据集上都具有最佳测试性能，且在上半部分中，SSPCA的一致率表现一般也是在G241c数据集上得到的，其可能的原因是，G241c 数据集上的数据分布可能本身具有明显的类簇特征以及噪声数据较少现象，TSVM 方法处理的数据正好是需要这样的数据分布和数据特征。当有10 个带标签的实例时，在个别数据集上，SSPCA 并没有比SSCCM 更好。一个可能的原因是数据集上的数据分布本身比较有规则，噪声数据较少，而无法体现SSPCA 的优势。由此可见，SSPCA 对具有参杂噪声数据或者是异常数据的数据集来说可能分类效果更佳。尽管如此，SSPCA 在6 个数据集中的3个数据集上均达到最佳测试性能；并其平均性能也是最佳，一致率均接近1。然而，在100 个带标签实例的情况下，SSPCA 在其中的4 个数据集上性能均达到最佳，并且在平均性能上也是最佳；同样，一致率均接近1，而一致率最低为0.987 6是在BCI数据集上得到的。很重要的一点是，通过在原SSCCM 方法上增加模糊熵的聚类假设后，在大多数数据集上，SSPCA的性能均优于SSCCM，这表明模糊熵的加入对于半监督分类中克服噪声或者异常数据的影响是很显著的。

6.4 SSPCA与hard-SSPCA进行比较

表4 显示了SSPCA 和hard-SSPCA 在二分类UCI 数据集上的比较结果，比较表4和表5的测试结果，可以看出SSPCA 在多类分类问题上略优于在二类分类。虽然，在个别数据集上方法hard-SSPCA 的测试性能略优，其结果差距也是微乎其微。从表4～6 整体上来看，在其他数据集上，方法SSPCA 的测试性能和平均测试性能均优于方法hard-SSPCA。这一结果表明，加入了基于隶属度的SSPCA分类方法体现了其有效鲁棒性。

表4 hard-SSPCA和SSPCA在二类UCI数据集上的性能比较

表5 hard-SSPCA和SSPCA在多类UCI数据集上的性能比较

表6 hard-SSPCA和SSPCA在基准数据集上的性能比较

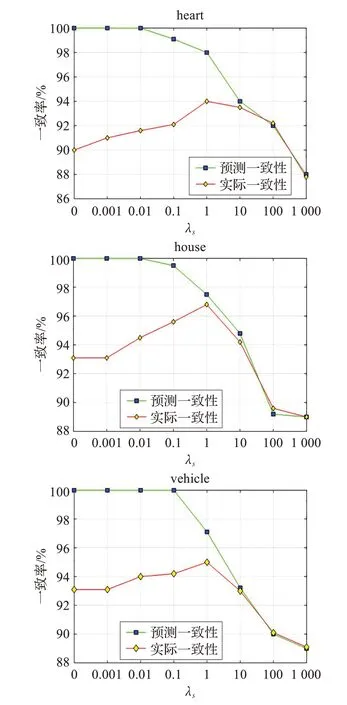
图2 对于不同λs值，w(x)和f(x)之间的预测和实际（本质）一致率比较

6.5 一致性分析

图2 为在6 个UCI 数据集上对应于不同λs值{0，0.001，0.01，0.1，1，10，100，1 000}的SSPCA 实际一致率的实验结果。在图2 中，当λs足够小时，预测一致率可以达到1，然后随着λs的增加而一致率逐渐降低，由于间接一致性实例变成了不一致性实例，最终变得与实际一致率相等了。同时，直到λs变为1，然后减小时，实际一致率增加，原因可能是当λs远小于或大于1时，SSPCA的目标将更多地集中在数据或者在数据的LWM 的分类上，而不是在它们的预测一致性上。

7 结束语

在现有研究基础之上，本文提出了一种基于可能性聚类的半监督分类方法。其经过模糊熵正则项的加入，增大样本的判别信息量，通过学习得到一个更具泛化性的分类模型，从而克服了噪声和异常数带来的负面影响来提高该方法的鲁棒性。所提方法SSPCA 与最新的半监督分类方法以及hard-SSPCA 在真实数据集上进行实验比较，验证了所提方法SSPCA 的分类可靠性、鲁棒性以及两个函数的预测一致性。然而，在优化过程中如何选择一个有效的核函数/核空间以及如何在理论上进行分析论证所提方法的一致性都是本研究值得更深层次探讨的问题。