万有引力与群体状态自适应的智能优化算法

许瀚誉，冯 翔，虞慧群

华东理工大学 信息科学与工程学院，上海200237

1 引言

如今，随着云计算、物联网和人工智能等技术的兴起，数据正以爆炸式的速度不断地增长和累积，标志着大数据的时代已经到来[1]。在大数据时代，模式分类有着广泛的应用前景。现实生活中的很多问题都可以转化成模式分类问题。面对数据量的增大、数据维度的变大以及数据结构的复杂化，传统的模式分类模型面临越来越多的挑战。近些年，用启发式算法优化现有的模式分类算法，在实际应用中取得很好的效果。例如，与一些分类准则结合构造分类器，或者训练多层感知器用于地震预测等[2]。自然启发式算法是根据确定性规则或者随机性来模拟自然界中生物和物质的行为。比如，模拟鸟群和鱼群社会行为的粒子群算法（PSO）[3]；模拟蜜蜂合作行为的人工蜂群算法（ABC）[4]；模拟细菌觅食行为的细菌觅食算法（BFOA）[5]；模拟萤火虫闪烁行为的萤火虫优化算法[6]；模拟布谷鸟生活方式的布谷鸟优化算法（COA）[7-8]；模拟蚂蚁群体觅食散发信息素行为的蚁群优化算法[9]以及模拟天体间引力的万有引力算法[10]等。但是，现有的自然启发算法具有群体构建和群体优化操作单一的缺点，所以收敛速度较慢，鲁棒性和稳定性不高，对传统的模式分类模型的优化能力也有限，不能满足问题和应用需求。例如PSO[11-12]，它不能有效地探索整个解空间，所以往往会陷入局部最优或失去多模态问题最优解的多样性。为了解决这个问题，一些算法使用控制参数来影响算法的搜索能力。它们的策略是将算法逐步从全局搜索转变为局部搜索。一般来说，这是正确的，但是有时很难解决某些问题，例如具有许多最优值的多模态函数，因为它们过早地进行了局部探测。也有其他方法使用调整种群大小来控制探索和探测之间的平衡，虽然这种方式可以简单地保持多样性，但它通常会得到一个不满意的最优解。因此，提出新的自然启发式算法是十分有意义的。

物质是由群体组成，群体状态自适应也是一种自然启发和优化的过程[13]。从宏观角度，物质在特定环境的作用下，总是从一个不稳定的状态转换到一个相对稳定的状态。从微观角度，物质是由粒子组成的，粒子受到特定环境的作用，总是趋向于彼此间距离更小，引力更大。这种群体状态自适应的现象，既符合优化问题的一般规律，也可以应用在对数据的处理问题中。

在物理世界中，引发群体状态变化的环境因素主要有两种，温度和引力。本文以万有引力为环境条件模拟群体状态自适应的优化过程，用于分群和群体优化过程中全局搜索和局部探测的控制，并受化学反应算法（CRO）[14]的启发，提出四个种群操作子模型丰富群体内部连接。除了上述贡献外，本文理论分析了算法的收敛性，并在函数极值实验中验证了提出的模型的有效性，证明了模型具有收敛速度快和鲁棒性高的特点；将提出的模型结合欧式距离准则，提出新的最小距离分类模型，在UCI 数据集实验中与其他经典的模型相比较，体现了提出的模型在大数据应用中的潜力。

2 问题模型

本文将处理两个问题，连续优化问题和模式分类问题。由于最小化问题和最大化问题可以很容易地相互转换，在本文定义一个全局优化问题如下：

其中，f(X)为全局优化问题的适应度函数，对于最小化问题，如果f(X)越小，那么对应的优化效果就越好。对于一个具有n 个变量的优化问题，本文用一个n 维矢量来表示问题的解，S 为此优化问题的可行域。那么，全局优化问题的关键就是寻找一个解X*，使得：

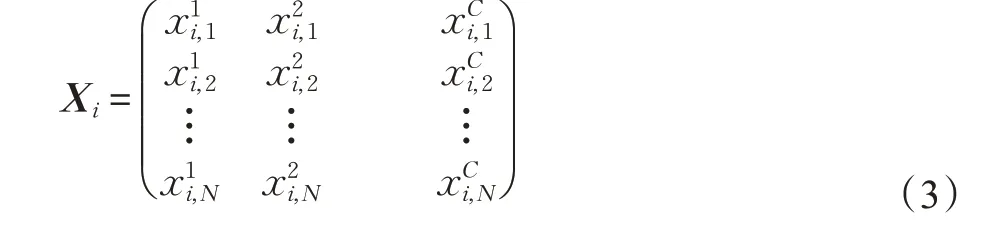
在模式分类问题中，本文是构造基于距离的分类器。所以，如果一个数据集具有C 类样本，每个样本具有n个类属性，可以将C 个类中心表示为下面公式所示的n×C 维矩阵。其中，列向量表示为该类对应的类中心。这样，分类模型求解过程可以被视作在n维空间中寻找C 个最优类中心的优化问题。

在求解最优类中心的过程中，本文将从文献[15]给出的三个适应度函数中选取一个作为本模型的适应度函数，用于评价当前的分类模型。

其中，DTrain表示训练样本的个数；CL(Xj)表示为根据当前的分类模型，样本j应当被划分的类别；CLknown(Xj)表示为数据集中样本j 的目标类别；表示为第k 类的类中心；d 则为两点之间的欧式距离。

3 算法模型与算法设计

3.1 算法物理模型

物质一般存在三种基本状态：气态、液态和固态。物质是粒子以群体形式的体现且群体状态会根据环境发生变化。在恒温的环境下，力就是引起群体状态自适应的唯一因素。在诸多力的计算公式中，最能表现群体状态自适应的是万有引力[10]。本文将问题的解空间看作群体状态自适应的环境空间，问题的最优解就是环境空间里的最优粒子，最优粒子将提供群体状态自适应的所需的因素，也就是粒子运动的引力，且在环境空间中最稳定的物质状态是固态。因此，问题求解的过程，初始的群体粒子，受到最优粒子的引力作用，与其距离越来越近，作用力也越来越大，物质的状态从气态逐步变化到最稳定的固态。

群体状态自适应模型的物理模型如图1。每一个小的粒子都是解空间的一个解。蓝色表示气体粒子，红色表示液体粒子，绿色表示固体粒子。其中带有数字的白色圆圈分别代表四种粒子运动方式。

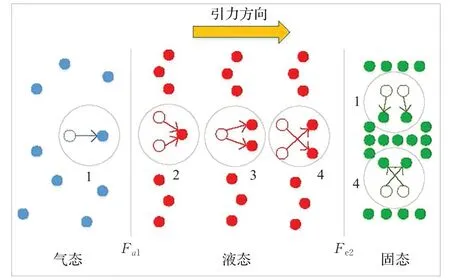
图1 群体状态自适应模型图

3.2 引力策略

在演化算法中，群体的构建和优化过程中全局探测和局部探索的平衡控制是十分重要的部分。在提出的算法中，使用万有引力模型进行群体的分群和判断群体中个体的状态，从而实现群体内部信息的充分利用和优化过程中探索和探测的平衡。首先算法在气体状态下主要是采取单粒子自撞运动，进行全局寻优操作，寻找优化最快的方向；然后算法在液体状态下主要是采取双粒子融合运动、单粒子分裂运动和双粒子交叉运动，全局寻优和局部寻优保持一个平衡状态，保证收敛速度的同时也保证优化的多样性；最后算法在固体状态下主要是采取单粒子自撞运动和双粒子交叉运动，进行局部寻优操作，精化问题的最优解，但是同时也保持跳出局部最优值的能力。在G-CSAO 中引入万有引力模型，计算公式为：

其中，G0=6.67×10-11是引力常数；m0是最优粒子的质量，为了计算方便设置为；M 是群体中粒子的质量，大小与粒子的适应度函数f(X)有关，在提出的算法中M=e-f(X)；r 是群体中粒子与最优粒子的距离，大小也是与适应度函数f(X)有关。最终，将各个因子代入公式（1），在提出的G-CSAO 中万有引力模型的公式为：

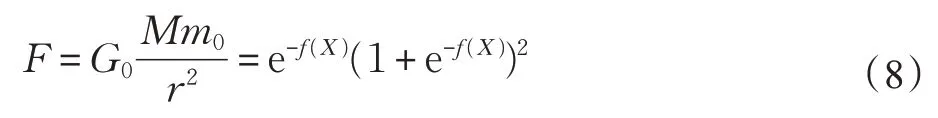
大部分演化过程和优化算法都是通过将现有解添加扰动来寻找新的解的方法进行邻域搜索操作。假设要处理的问题的维度间是相互独立的，不存在彼此间的约束条件。邻域搜索操作中的扰动有很多可以选择的概率分布函数，提出的算法将采用最常用的Gaussian 概率分布。它的概率密度函数为：

这里μ是平均值，σ2是方差。扰动操作包含三个组成部分，初始点、方向和步长。在G-CSAO 中初始点就是粒子结构。因为并不知道问题的全局最优解，所以并不知道方向，Gaussian 概率分布是均匀的，将μ=0 可以使得扰动的方向是等概率的。此外，σ 影响μ传播的宽度，σ 越大，扰动越大，因此σ 是模型中步长（不同物质状态时不同，一般液态为气态的十分之一，固态为气态的百分之一）。那么，新的粒子结构X′中的第i维可以表示为：

3.3 单粒子自撞运动

如图1中圆圈1所示，在G-CSAO 中，粒子会吸引在同状态下的微小粒子，结合自身的运动发生自撞运动，使得自身的质量变大，形成新的粒子。具体是在粒子群体Pop 中选择一个粒子通过万有引力模型计算粒子与最优粒子之间的引力大小F，如果F 满足下面约束条件中的一条，就对X 进行单粒子自撞运动算法。

其中，Fθ1是气态和液态的阈值，Fθ2是液态和固态的阈值，λ是一个随机数，λ ∈(0,1)。单粒子自撞运动算法的公式如下：

xi是粒子结构X=(x1,x2,...,xi,...,xn)中的一维，i ∈[ 1,n]。如果新得到的粒子解比原粒子的解好，那么就保留新的粒子结构，否则：

之后再对粒子结构中的其他维进行相同的操作得到最终的新粒子结构，放入到群体Pop中，保持群体大小不变。

算法1单粒子自撞运动

Input：one X in Pop

while i ≤n do

x′i=xi+η(0,σ2)

If f(X′)≤f(X)

x′i=xi-η(0,σ2)

end if

end while

Output：new X′in Pop

3.4 双粒子融合运动

如图1 中圆圈2 所示。在群体状态自适应过程中，前一个状态中的两个粒子通过相互吸引和相互碰撞，距离越来越靠近，最后融合成为一个新的粒子。双粒子融合运动算法首先在粒子群体Pop 中选择一个粒子进行万有引力模型计算引力大小F，如果F 满足下面约束条件：

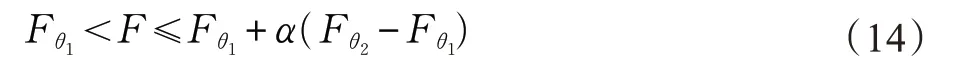
算法2双粒子融合运动

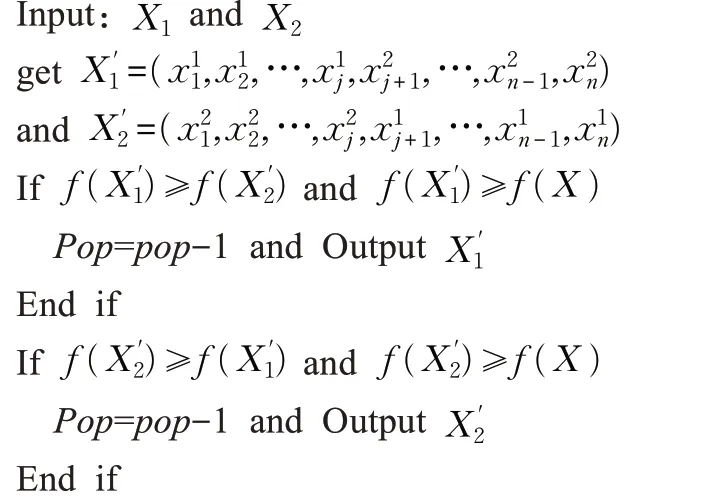
3.5 单粒子分裂运动

如图1中圆圈3所示。当物质在固定环境中达到稳定状态的过程中，群体中质量较小的粒子受到群体中质量较大的粒子的引力作用，可能会发生粒子分裂现象，分裂的两部分会慢慢向质量大的粒子靠近，最后成为两个新的粒子。新的粒子与最优粒子的引力更大，更加靠近最优粒子。单粒子分裂运动算法首先在粒子群体Pop 中随机选择一个粒子X 且不是群体中适应度值最小的粒子Xopt，进行万有引力模型计算引力大小F，如果F 满足下面约束条件：

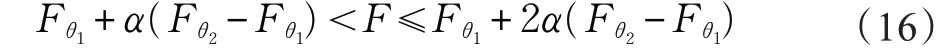
对X 进行单粒子分裂运动算法。具体操作如下：

如果f(X1)＜f(X)，那么对X1中粒子结构是X 的部分进行单粒子自撞运动：

得到的新的粒子X1；如果f(X1)＜f(X)，那么对X2中粒子结构是X 的部分进行单粒子自撞运动：

将最终得到的两个粒子X1和X2放入群体中，群体的大小加1。

算法3单粒子分裂运动

3.6 双粒子交叉运动

如图1中圆圈4所示。在物质状态渐渐接近稳定状态的时候，处于同一状态下的两个粒子受到相互之间的引力作用，会发生相互碰撞，两个粒子的内部结构会发生交叉，得到两个新的粒子。双粒子交叉运动算法首先在粒子群体Pop 中选择两个粒子X1和X2，通过万有引力模型分别计算与最优粒子间的引力大小F1和F2，如果满足下面两个约束条件中的一个：

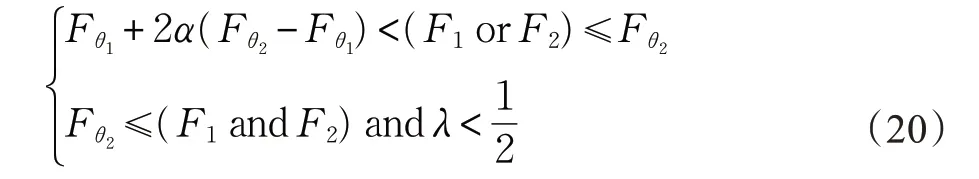
那么就对X1和X2进行双粒子交叉运动算法，具体操作如下：

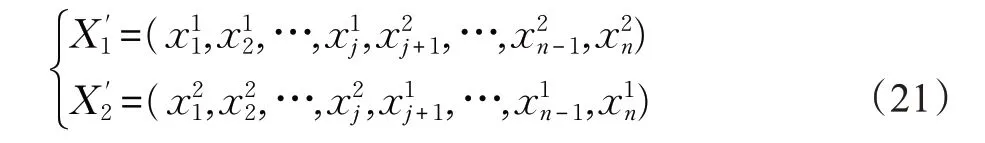
算法4双粒子交叉运动

提出的算法的流程图如图2所示。

4 理论分析

根据Lyapunov 的第二稳定性理论，将G-CSAO 的四种粒子运动考虑成一个系统方程x′=f(x,t)，且稳定状态为x0=0。定义如下：如果一个正定函数V(x,t)是连续的一阶偏导，满足下面的条件：

图2 G-CSAO算法流程图

（1）若V′(x,t)是负定的，那么这个系统在x0=0的状态是一直逐渐稳定的。

（2）推 广 可 得，随 着||x||→∞，那 么 就 有V(x,t)→∞，那么这个系统在x0=0 的状态是大致逐渐稳定的。

对于G-CSAO的数学模型，可以定义为一个Lyapunov的系统L(R(t))。

5 实验模拟与分析

本文根据问题模型，将实验模拟分为两个部分：全局优化问题的函数极值实验和模式分类问题的UCI 数据集实验。在函数极值实验中，主要验证G-CSAO 模型收敛速度和鲁棒性等，以及在数据高维度下的优化能力；在模式分类实验中，将基于G-CSAO 的最小距离分类器同经典的机器学习算法相比较，测试G-CSAO模型在大数据问题中的潜能。本文实验环境为：Intel Core Quad 2.7 GHz CPU；8 GB RAM；G-CSAO 模型在Windows 10环境下用C++编码。

5.1 函数极值实验

为了测试G-CSAO 模型的全局优化能力，本文选取常用的10 个具有代表性的基准函数[16]进行验证，基准函数如表1。根据基准函数的峰值特征不同，10 个函数可以分为两类：一类是单模函数f1～f5，一类是多模函数f6～f10。

在G-CSAO 模型中有5 个可调参数，分别是Pop、epoch、σ、Fθ1和Fθ2。为了保证实验的公平性，在10 个函数极值测试中，G-CSAO 的参数也保持不变，设置为（20，10 000，10，1，5.5）。

表1 基准优化测试函数

为了能相对地了解G-CSAO 模型的优化能力，将G-CSAO 同5 个经典的自然启发算法作比较，分别是RCCRO[16]、DE[17]、PSO[3]、ABC[4]以及CMAES[18]。在实验中，同样对各个算法做参数分析，遵循与文献[13]一样的标准。对每一个测试函数，算法将运行30 次得到平均值做对比，最优结果用粗体标出。

从表2 的对比结果和图3 迭代曲线分析可以得出，G-CSAO 在单模和多模都有不错的效果，在单模实验中，除了在f1、f2、f3的表现略逊于CMAES；在多模实验中，在f7的结果也是仅次于CMAES。从综合排名可以看出，G-CSAO 的排名为第一，说明G-CSAO 模型在全局优化问题的综合表现是非常好的，具有收敛精度高，稳定性好的特点。

为了更加直观地了解G-CSAO 模型的特点，观察G-CSAO 在宏观下群体状态自适应情况和微观下粒子运动情况。根据G-CSAO 模型的属性，刻画出G-CSAO求解f1的实验过程。在同一时刻下，其中x轴为群体中所有粒子的合力的倒数，y 轴为群体中所有粒子的质量均值倒数，z 轴为群体中所有粒子与最优粒子的平均距离，原点的坐标为（0，0，0.5），如图4所示。

表2 函数极值实验寻优结果

图3 六种算法的迭代寻优曲线图

图4 G-CSAO算法在宏观和微观视角中群体运动过程

5.2 UCI数据集实验

在模式分类实验中，将基于G-CSAO 模型和最小距离分类模型来构造一个分类器。并使用12 个UCI 数据集来测试该分类器的性能。在本实验中，G-CSAO 的参数设置与极值测试一致。首先，将使用问题模型中提到的三个适应度函数来分别测试G-CSAO 在各数据集上的性能。之后，将选出在某个适应度函数下分类效果最好的一组实验结果，将其与经典分类算法进行比较。对比算法的实验数据来自文献[15]。为了保证可比性，本文中，使用5 折交叉验证，采用随机抽样的方式将各数据集分为5等份，每次抽取其中4份作为训练集，剩下的1 份作为测试集。取5 次实验结果的平均值，作为最终实验结果。为了有效使用欧式距离来区分各样本的差异度，对各维度已经转化实数的数据集进行归一化处理。归一化方法如下所示：

其中，xij表示数据集中第i 个样本的第j 个属性。归一化后，各数据集各样本的属性值都在[0，1]之间。在实验中，使用错分率作为最终分类效果的评价标准，如下所示：

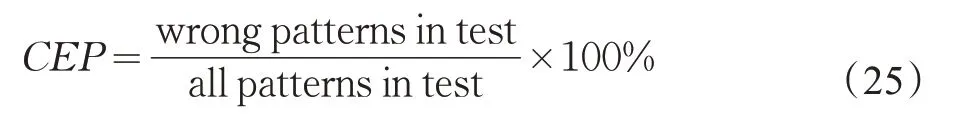
表3 列出了G-CSAO 使用不同的适应度函数时在各数据集上的实验效果，最好的实验结果被加粗列出。

从表中的数据可以看出，当G-CSAO 采用适应度函数f3，平均效果是最好的。因此，在实验中将使用f3时的实验结果与其他算法进行对比。

从表4 列出的数据可以看出，G-CSAO 在Iris、Cancer、Heart、Balance 和Diabetes 等5 个数据集上的效果都是最好的，在Thyroid和Wine数据集上，G-CSAO的表现仅次于MlpAnn，在Cancer-Int 数据集上，G-CSAO的表现比MltBoost 算法差。在Credit 和Horse 数据集上，G-CSAO 的效果仅次于Bagging。在Dermatology 数据 集 上，G-CSAO 的 效 果 要 比MlpAnn 和Bagging 差。G-CSAO 在Glass 数据集上的效果比较一般。综合来看，基于G-CSAO 构造的分类器在这12 个数据集上取得了不错的效果。

表3 不同适应度函数的分类错误率%

6 结束语

在大数据的时代背景下，当传统的优化算法和模式识别算法并不能满足人们对数据分析的需求时，本文提出一种新型的自然启发模型（G-CSAO），模拟群体状态自适应中逐渐达到稳定状态的过程，并与最小距离规则相结合形成新的模式分类分析模型。通过函数极值实验，多角度的分析，验证了G-CSAO 的有效性和稳定性；通过UCI数据集实验，测试了G-CSAO 在模式分类问题中的性能，以12个数据集的分类结果同8个经典的模型相比较，具有不错的表现。说明G-CSAO 在大数据应用中有很好的潜能。

伴随着网络大数据的飞速发张和扩张，本文提出的G-CSAO 模型能够应对优化问题复杂，数据量增大，数据维度变大和数据结构多样性的情况。在对图像、语音识别等领域将会是G-CSAO 今后的研究重点，希望可以在演化行为领域做出更大的贡献。

表4 各算法在12个UCI数据集上的分类错误率 %