近距二次反射法测量金属丝杨氏模量

胡训美，张 波

(皖西学院 基础实验中心，安徽 六安 237012)

在静态拉伸法测量金属丝杨氏模量实验中，为了提高光杠杆的放大倍数，通常要求尺读望远镜与光杠杆的镜面水平相距距离在1米以上[1]。这导致杨氏模量测量仪在实际使用过程中需要占用较大空间。此外，外加砝码时由于人为因素会导致金属丝抖动，从而产生读数误差。针对这些问题，本文利用近距二次反射法测定金属丝杨氏模量，把横向水平镜尺距离转化为纵向垂直距离，利用光杠杆与平面镜间的二次反射增加光程，从而完成对金属丝微小变化量的测量。这不仅节省了仪器占用空间，而且通过数字式施力计代替外加砝码改变金属丝拉力，减小了外在人为因素导致的实验误差。

1 静态拉伸法测量金属丝杨氏模量的实验原理

设一根粗细均匀的金属丝，在受到沿长度方向的外力F的作用下产生形变，其形变量为ΔL，根据胡克定律：

(1)

式中L为线性长度，S为横截面积，比例系数Y即为金属丝的杨氏模量(单位：N/m2)。对于直径为d的金属丝，其杨氏模量为：

(2)

在L、d和F相同的情况下杨氏模量Y越大的金属丝，其伸长量ΔL越小，常用的测量工具难以对ΔL进行测量，实验中需要用光杠杆进行放大测量[2]。

1.1 传统光杠杆放大原理

如图1所示，将光杠杆的前足尖固定在平台上的凹槽中，后足尖放置于金属丝活动夹表面，当外加砝码时，金属丝在外力作用下改变了ΔL微小长度，此时光杠杆镜面偏转θ角度，反射光线改变2θ角度，从望远镜里观察到的标尺刻度从初始位置由R0变化到R1的位置。由图中的几何关系可知

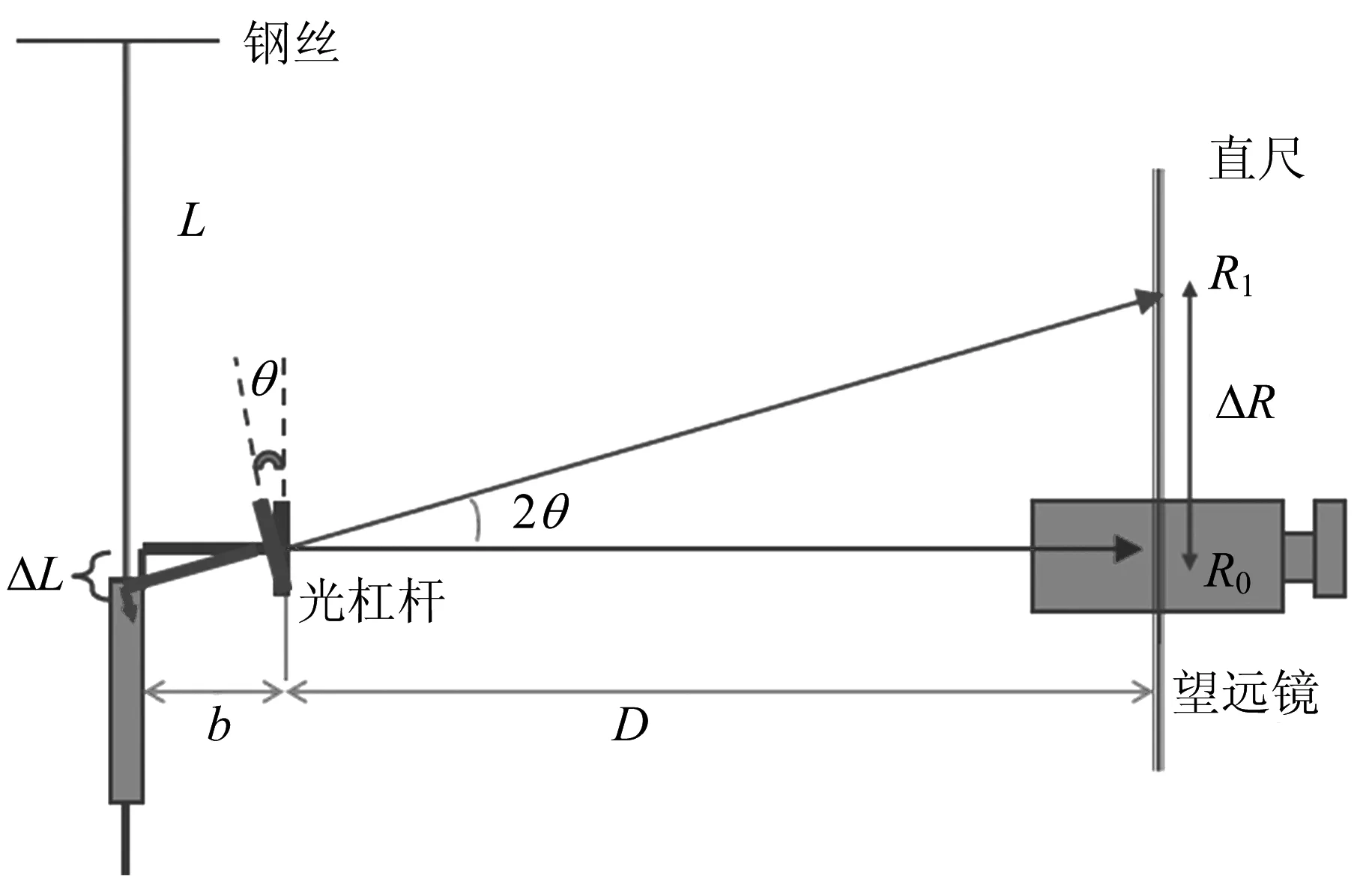
图1 光杠杆原理图

(3)

(4)

式中b为光杠杆的臂长，D为镜尺距离，ΔR为加上外力以后望远镜里标尺刻度的改变量。由于角θ很小，tanθ≈θ，tan2θ≈2θ，所以

(5)

(6)

由(5)式和(6)式可消去θ，得

(7)

将(7)式代入(2)式得

(8)

光杠杆系统的放大倍数为：

(9)

从(9)式中可以得出，D越大光杠杆系统放大倍数β越大。但在具体实验过程中由于场地、仪器等因素影响了镜尺距离D的大小，从而直接限制了光杠杆放大倍数，影响了实验中的测量精度。因此需要对传统实验中所用到的杨氏模量测量仪器进行改进。

2 近距二次反射法测量金属丝杨氏模量

2.1 杨氏模量测量仪器的改进

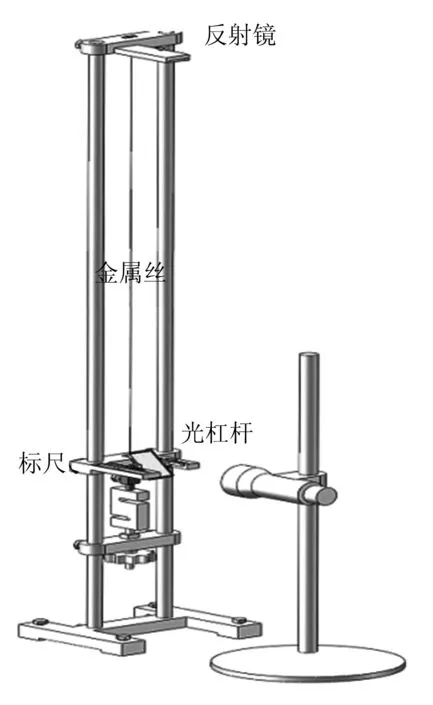
图2 近距二次反射法杨氏模量测量仪示意图

如图2所示，将待测金属丝一端固定在杨氏模量测量仪的顶部夹具上，金属丝另一端穿过活动夹头与施力计相连。顶部夹具上装置一平面反射镜，标尺和光杠杆平台处于同一平面上，且标尺位于光杠杆平台的一侧。光杠杆平台上的刻度尺发出的光通过顶部夹具上平面反射镜反射至光杠杆镜面，经光杠杆镜面反射到达望远镜视场中[3](P11)。这种改进将传统仪器中横向水平镜尺距离转化为纵向垂直距离，打破了水平空间对测量精度的限制。

2.2 近距二次反射法测量微小位移原理

如图3所示，调节光杠杆镜面使得镜面法线与水平方向成一夹角(45°)，再调节望远镜直至在望远镜视场中看到清晰的标尺示数x1的像。通过施力计对金属丝施加外力，待测金属丝在施力计的作用下产生的微小位移为ΔL[4]，此时光杠杆动足尖下降从而带动光杠杆镜面转动角度为θ，根据光的反射定律可知，在出射光线(即进入望远镜的光线)不变的情况下，入射光线相应转动了2θ角度，此时在望远镜中观察到标尺示数变为为x2，标尺示数的改变量为Δx。

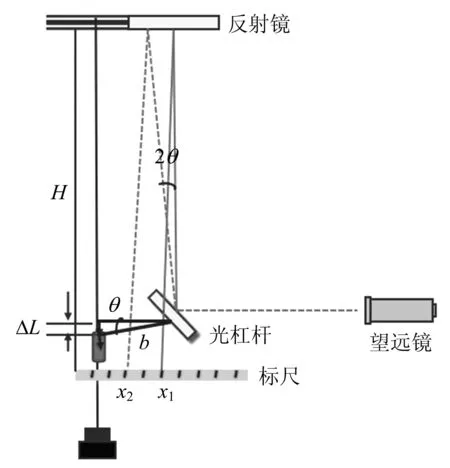
图3 近距二次反射法光杠杆放大原理

从图3的几何关系中我们可以看出，

(10)

(11)

式中H是上夹具上固定的反射镜转轴到光杠杆平台上标尺间纵向垂直距离，实验中H≫ΔL，且在外力作用下金属丝的微小变化量所导致的光杠杆转动θ角很小[5]，所以有：tanθ≈θ,tan2θ≈2θ

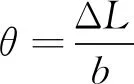
(12)

(13)

故有：

ΔL=b·θ

(14)

Δx=2θ·2H

(15)

联立(14)和(15)式消去θ,得

(16)

仪器中4H≫b，这样一来，便能把一微小位移ΔL放大成较大的容易测量的位移Δx。将(16)式带入(2)式得到：

(17)

如此，可以通过测量(17)式右边的各参量得到被测金属丝的杨氏模量，式中各物理量的单位取国际单位(SI制)。

2.3 改进后的光杠杆及放大倍数

改进后的光杠杆其反射镜转动轴线在光杠杆镜面内，动足尖自由放置在活动夹头表面。光杠杆的臂长为反射镜转轴中心点到动足尖的距离，可自由调节[6]。光杠杆镜尺系统的放大倍数为：

(18)

由(18)式可知，改进后的近距二次反射法测量杨氏模量装置中其光杠杆镜尺系统的放大倍数仅与纵向垂直距离H和光杠杆的臂长b有关，与望远镜和杨氏模量测量仪的水平距离D无关。

3 实验测量结果及分析

3.1 碳钢丝直径测量数据

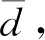
表1 金属丝直径的测量

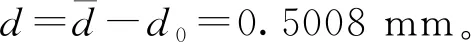
3.2 光杠杆常数及金属丝长度的测量

用钢卷尺测量碳钢丝的原长L，即金属丝的上夹头下表面到平台活动夹的距离。用钢卷尺测量镜尺距离，即反射镜转轴镜面到标尺的垂直距离H。用游标卡尺测量光杠杆臂长b，即水平卡座长度。用钢卷尺测量出望远镜与光杠杆镜面距离D，见表2。

表2 光杠杆常数及碳钢丝长度的测量

3.3 测量标尺示数x的值

1)按实验装置示意图装置好仪器，调节望远镜直至在望远镜视场中看到清晰的标尺刻度像；

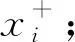
3)缓慢旋转施力螺母，逐渐增加碳钢丝的拉力，每隔0.50 kg记录一次标尺示数，直至设定值；

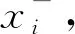
5)求出标尺示数改变量Δx值，见表3。

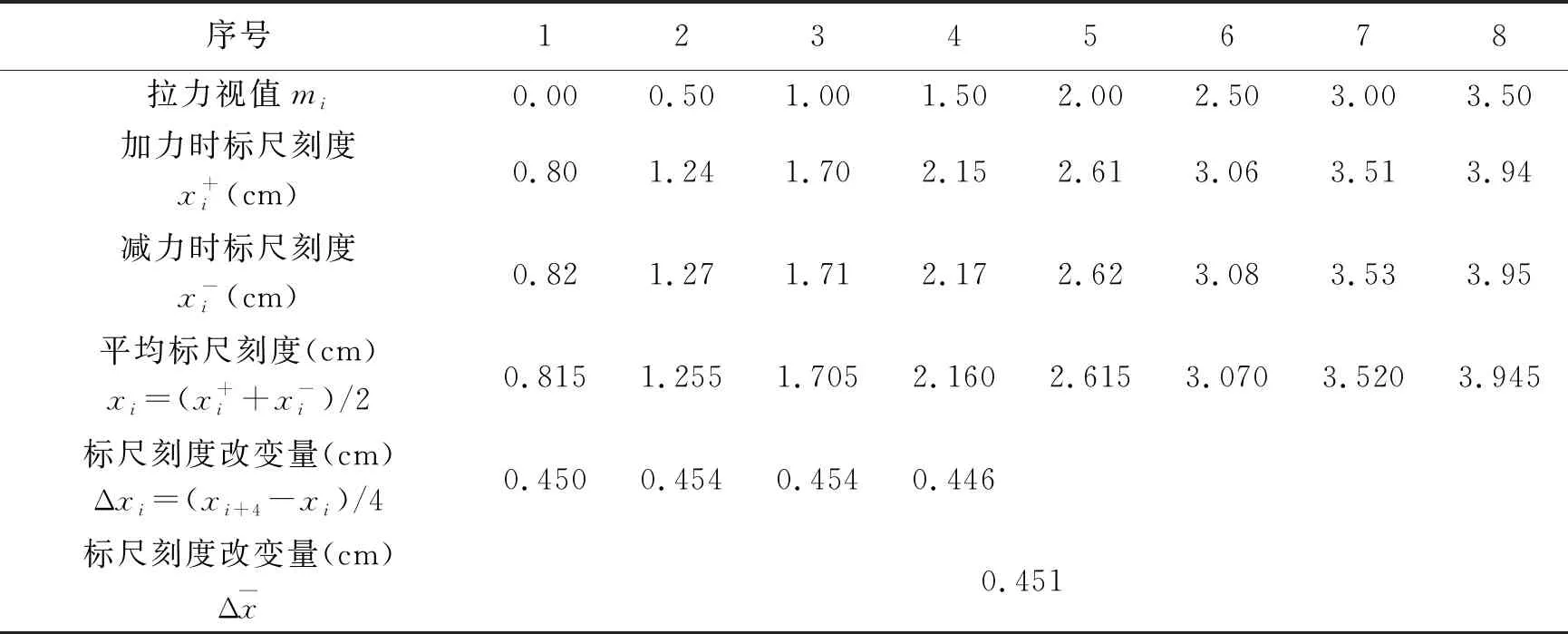
表3 标尺示数x的值

3.4 测量结果

将表1—表3的测量数据带入(17)式中，则利用本装置测得的碳钢丝杨氏模量结果为：

Y=2.02×1011(N/m2)

对标准不确定度U(Y)进行评定，U(Y)=1.854×109(N/m2),写出金属丝杨氏模量的结果表达式为：

Y=(2.02±0.02)×1011(N/m2)

碳钢丝在20 ℃时杨氏模量的理论值为(2.0×1011—2.1×1011)N/m2，测量结果在误差范围内，由此可见测量结果准确。

4 结语

本文利用近距二次反射式杨氏模量测量仪器，把横向水平镜尺距离转化为纵向垂直距离，在测量过程中不仅缩短望远镜与实验仪器之间的距离，节省仪器占的用空间，而且有效地提高了光杠杆的放大倍数。实际测量所得到的实验数据准确、误差小，提高了实验精确度。