收入差距对我国消费需求影响的理论和实证研究
——基于不同收入群体基尼系数的分析
陆前进,武 磊
(1.2.复旦大学 经济学院,上海 200433)
引言
为研究国民收入在国民之间的分配问题,美国经济学家洛伦茨(Max Otto Lorenz,1876—1959)1905年提出了著名的洛伦茨曲线。他将一国人口按收入由低到高排队,然后考查从低到高的任意人口百分比所得到的收入百分比,将这样的人口累计百分比和收入累计百分比的对应关系描绘在图形上,即得到洛伦茨曲线。洛伦茨曲线反映了收入分配的不平等程度,弯曲程度越大,收入分配越不平等,反之则反①。一般来说,一个国家的收入分配,既不是完全不平等,也不是完全平等,而是介于两者之间。相应的洛伦茨曲线,既不是折线,也不是45度线,而是向横轴凸出的弧线。本文根据洛伦茨曲线的特点,采用三角函数形式的洛伦茨曲线对其拟合,进而分析不同群体的收入差距。
将洛伦茨曲线与45度线之间的部分叫做“不平等面积”,不平等面积与完全不平等面积之比,称为基尼系数,常作为衡量一国贫富差距的标准,其取值范围为[0,1]②。 本文根据三角函数洛伦茨曲线的特点,利用极限方法进一步得到低收入群体和高收入群体的基尼系数,基尼系数实际上是相应参数值的函数,并据此来分析不同群体的收入弹性。
一、文献回顾
(一)国外研究文献综述
从国外文献对洛伦茨曲线和基尼系数的研究来看,Ortega et al.(1991)[1]构建了一种新的函数形式,能够比较容易计算出基尼系数等多个不平等系数。Ogwang et al.(1996)[2]也构建了一种新的函数形式拟合洛伦茨曲线,且基尼系数形式简单,拟合效果较好。Ogwang et al.(2000)[3]还考虑到传统的洛伦茨曲线的缺点,构建了混合的洛伦茨曲线,一种是加法形式的混合模型;另一种是乘法形式的混合模型,比较发现加法形式和乘法形式的混合模型效果都较好。Farris(2010)[4]给出了基尼系数的几种解释,根据洛伦茨曲线,该文研究了不同人口百分比下的平均收入,并且比较了较低收入群体的收入与平均收入的差距。Wang et al.(2015)[5]考察了一个双参数的洛伦茨曲线,并分析了它的曲率,进而构建了洛伦茨曲线的混合模型,用美国数据进行拟合,发现效果也较好。
(二)国内研究文献综述
从国内文献对洛伦茨曲线和基尼系数的研究来看,程永宏(2007)[6]认为我国总体基尼系数自1992年以来一直大于或等于0.4,城镇基尼系数及其贡献率增长最快。胡志军 等(2016)[7]认为我国城镇基尼系数有下降的趋势,农村基尼系数较稳定。刘长庚 等(2012)[8]测算了农民各类收入的基尼系数及其分解结果和贡献率情况。任媛 等(2016)[9]运用基尼系数及其相应的分解方法,对我国农村居民收入的区域差异问题进行研究。聂荣 等(2015)[10]通过Dagum基尼系数方法对农村居民收入分配的地区差距进行了测算,结果表明,农村居民收入分配在样本考察期内的总体差距呈现缓慢扩大趋势。李刚 等(2014)[11]研究表明基尼系数赋权法具有适用性强、保序性好的特点。吴建民 等(2011)[12]通过基尼系数把城镇居民收入差距分解为收入结构差距,揭示了工资性收入是总差距的决定因素。
(三)简短评述
从国内外现有文献来看,用三角函数拟合洛伦茨曲线,并分析不同群体的基尼系数的文献较少,本文的研究也是对洛伦茨曲线和基尼系数的有益补充。本文用三角函数来拟合洛伦茨曲线和估算不同收入群体的基尼系数,在此基础之上研究收入差距对我国消费的影响。本文的新意主要体现在三个方面:一是构建了三角函数形式的洛伦茨曲线拟合中国、美国的收入差距;二是根据相应的基尼系数计算公式,利用极限方法计算出低收入群体和高收入群体的收入弹性;三是构建了收入差距对消费影响的理论模型,并分析了城乡内部收入差距对消费的影响。
二、洛伦茨曲线、基尼系数与收入差距
(一)低收入群体的三角函数型洛伦茨曲线和近似基尼系数
由洛伦茨曲线图形的特点可知,洛伦茨曲线是凸向横轴的,在[0,1]之间,因此可以用非线性函数来拟合它③,如可以用正弦函数来拟合,因为正弦函数的值在0与1之间,图形也是凸向横轴的,符合洛伦茨曲线的特点。假定洛伦茨曲线的函数④为:
(1)
其中m是洛伦茨曲线函数的参数,随着m的变化,正弦函数的形状也会发生变化。m越大,函数越凸向横轴;m越小,函数越接近45度线(如图1)。

图1 不同m值下的洛伦茨曲线 图2 洛伦茨曲线与基尼系数
进一步可以计算基尼系数,45度线和洛伦茨曲线围成的面积与45度线和X轴围成的面积之比就是基尼系数(如图2)。

图3 从低收入群体出发看洛伦兹曲线
同时也可以观察到,任何一部分收入群体中收入不平等的基尼系数也是可以计算出来。根据图3可以看出,以低收入群体为起点,洛伦茨曲线通过原点,可以计算包含低收入群体的基尼系数,因此低收入群体基尼系数可计算为:

(二)低收入群体三角函数型洛伦茨曲线的非线性拟合、函数参数与收入弹性
根据洛伦茨曲线(1),本文采用OECD数据库提供的一国不同人口比例所对应的收入占比的数据,利用非线性回归的计量方法,对中国的收入差距进行了拟合⑤,回归结果见表1。

表1 洛伦茨曲线(1)对中国收入数据的回归结果
数据来源:根据OECD数据库和Eviews 9.0整理得到。
同样,利用OECD数据库中提供的美国的相应数据,还可以对美国的收入差距进行非线性拟合,回归结果见表2。

表2 洛伦茨曲线(1)对美国收入数据的回归结果
数据来源:根据OECD数据库和Eviews 9.0整理得到。
根据表1、表2的回归结果显示,本研究设定的三角函数形式的洛伦茨曲线无论是对中国的收入差距数据还是对美国的收入差距数据,非线性拟合的效果都较好,模型设定是较为正确的。

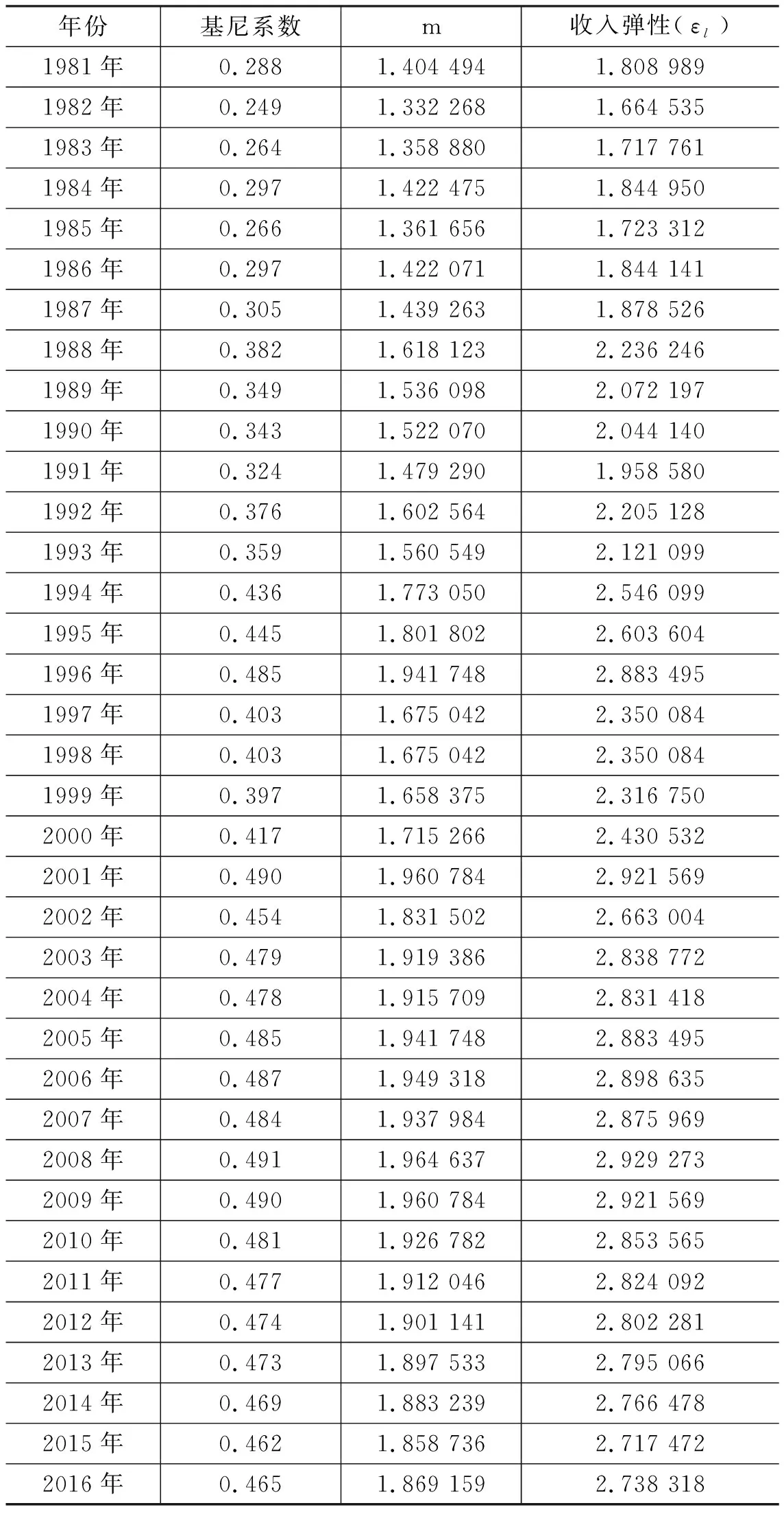
表3 中国的基尼系数,m和收入弹性
数据来源:国家统计局。
从表3可以看出我国居民收入弹性逐年的变化情况,数据表明我国的收入弹性均大于1,并且总体呈上升趋势,收入分配总体上越来越不公平。但值得注意的是,虽然我国居民的收入弹性总体上不断上升,但最近几年有所回落,这说明我国收入分配的不公平程度有减缓的倾向。
(三)高收入群体的三角函数型洛伦茨曲线和近似基尼系数
相反,从另一个角度来看,以高收入群体为起点,洛伦茨曲线通过(1,1)点,基尼系数都包含高收入群体。前面的洛伦茨曲线是单调递增的,增速也是上升的,但是还可能出现洛伦茨曲线是单调递增的,但增速是递减的,特别对高收入阶层更是如此,因此可以用下面函数拟合:
(2)
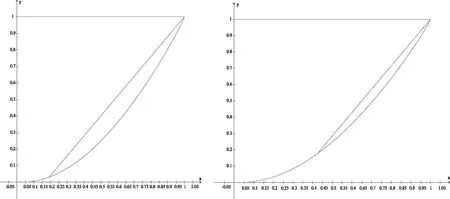
图4 从高收入群体出发看洛伦茨曲线
同时也可以观察到任何一部分收入群体中收入不平等的基尼系数也是可以计算出来。因此根据图4可以看出,以高收入群体为起点,可以计算包含高收入群体的基尼系数,因此高收入群体基尼系数可计算为:

(四)高收入群体三角函数型洛伦茨曲线的非线性拟合、函数参数与收入弹性
同样地,根据洛伦茨曲线(2),本文采用OECD数据库提供的一国不同人口比例所对应的收入占比的数据,利用非线性回归的计量方法,对中国的收入差距进行了拟合,回归结果见表4。

表4 洛伦茨曲线(2)对中国收入数据的回归结果
数据来源:根据OECD数据库和Eviews 9.0整理得到。
进一步,利用OECD数据库中提供的美国的相应数据,还可以对美国的收入差距进行非线性拟合,回归结果见表5。

表5 洛伦茨曲线(2)对美国收入数据的回归结果
数据来源:根据OECD数据库和Eviews 9.0整理得到。
根据表4、表5的回归结果显示,本研究设定的三角函数形式的洛伦茨曲线无论是对中国的收入差距数据还是美国的收入差距数据,非线性拟合的效果都较好,模型设定是较为正确的。
实际上,高收入群体收入变动的弹性可计算为:
=2n-1


表6 中国的基尼系数,n和收入弹性⑦
数据来源:国家统计局。
从表6可以看出我国居民收入弹性逐年的变化情况。数据表明,我国居民的收入弹性的总体趋势是在下降的,这意味着我国的收入分配总体趋势是越来越不公平的。同样值得注意的是,我国的收入弹性最近几年也是有所上升,这说明我国收入分配的不公平程度有减缓的倾向。因此无论是从高收入群体的方向来考察,还是从低收入群体的方向来考察,得到的基本结论都是一致的。
三、收入差距和消费
(一)收入差距对消费的影响
近年来,由于种种原因,我国居民的消费额在国内总产出中所占的比例正在快速地下降。2000年时,消费占我国当年度的GDP为48.17%,而到2012年时这一比例已下降至37.76%,下降了约10个百分点。虽然近些年来我国GDP在高速增长,也有一小部分人的收入增长确实十分快,并且大大快于同期GDP的增长,但是绝大部分居民的收入却增长较慢。总体而言,我国绝大部分居民的财富增长并不快。
我国居民消费总体上仍然较低,因为居民的储蓄s=(1-a)y,a为社会平均的消费倾向,y为居民收入。假设社会只有两个人,每个人每期的必需基本消费为c,所谓的必需基本消费即维持生活所必需的消费支出,即消费不能低于这一数额,否则将无法生活。两个人收入中只有超过c的部分,才会有一部分不被消费,而被储存起来。如果平均消费倾向越低,则消费下降,储蓄上升。
一般来讲高收入者的消费倾向低,而低收入者的消费倾向高,因此随着收入的增加,消费者的消费倾向是递减的,即边际消费倾向递减。用如下函数表示消费者的消费:当收入为y时,消费者的消费为c+(y-c)(1-b(y-c)),其中(1-b(y-c))是边际消费倾向,只要对系数b(b>0)进行适当的限制,该函数就满足消费函数的各种性质,随着收入增加,消费在增加,但是边际消费倾向递减。
居民总的收入为Y,两人各自的收入分别为y1、y2,y1+y2=Y,于是社会总的消费为:
C=c+(y1-c)(1-b(y1-c))+c+(y2-c)(1-b(y2-c))
上式化简后为:C=Y-b[(y1-c)2+(y2-c)2]
(3)
1.根据洛伦茨曲线(1)求解
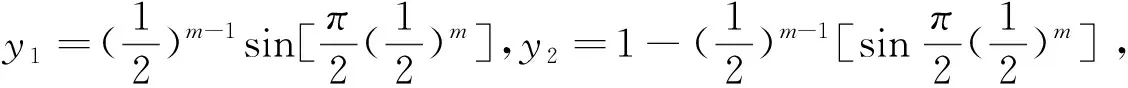

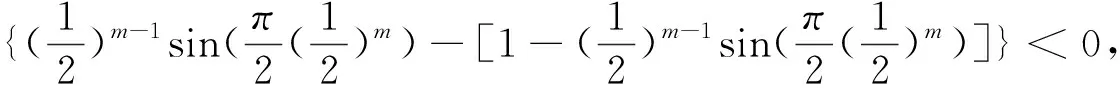
2.根据洛伦茨曲线(2)求解

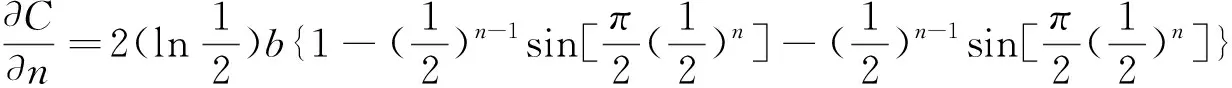

(二)混合的洛伦茨曲线和低收入、高收入群体的近似基尼系数
在前文的分析中假定每个人必需的基本消费支出是相同的,所以当收入绝对均等时,社会总消费量最大,这在同一地区内是成立的。但是如果考虑到各个地区,那么居民必需的消费支出就不同了,比如农村地区和城市就不同,各个城市之间也不同,如一个大城市和一个小城市相比较,其必需的生活支出数额肯定不一样。这样社会总消费在居民收入绝对均等时最大的结论很有可能就不再成立了。因此,接下来本研究分析在此种情况下,社会总消费何时最大?假设两个人处于国家的不同地区,其基本的生活消费分别为c1、c2(令c1 根据洛伦茨曲线变动的特点,本文综合上述两个洛伦茨曲线的变化,构建混合的洛伦茨曲线: (4) 可以得到低收入群体的基尼系数为: (5) 根据(5)式,进一步能够得到⑧: (6) 能够得到高收入群体的基尼系数为: 根据混合的洛伦茨曲线(4),本文采用OECD数据库提供的一国不同人口比例所对应的收入占比的数据,利用非线性回归的计量方法,对中国的收入差距进行了拟合,回归结果见表7。 表7 混合洛伦茨曲线(4)对中国收入数据的回归结果 数据来源:根据OECD数据库和Eviews 9.0整理得到。 进一步,利用OECD数据库中提供的美国的相应数据,还可以对美国的收入差距进行非线性拟合,回归结果见表8。 表8 混合洛伦茨曲线(4)对美国收入数据的回归结果 数据来源:根据OECD数据库和Eviews 9.0整理得到。 数据来源:Chen et al.(2010)[13];胡志军 等(2016)[7]。 数据表明,我国的低收入群体收入弹性在不断上升;高收入群体的收入弹性在不断下降,但最近有所上升。 根据前面的分析,社会的总消费:C=Y-b[(y1-c1)2+(y2-c2)2],其中: 对m,n求导: 综合以上分析可以看到,在一定的社会居民总收入下,居民收入差距越小,社会总消费量越大,收入差距增大将减小社会的总消费量。低收入居民之间的收入差距越大,社会总消费是下降的;低收入居民之间的收入差距越小,社会总消费是上升的,社会总消费随着低收入居民间收入差距的增加是下降的。同样高收入居民之间的收入差距越大,社会总消费是下降的;高收入居民之间的收入差距越小,社会总消费是上升的,社会总消费也是随着高收入居民之间收入差距增大而下降的。 毫无疑问,同一地区居民之间、不同地区居民之间的收入差距过大,导致社会总消费量迅速降低。在收入分配不均降低社会总的平均消费倾向,从而降低社会总消费的同时,大量社会单个个体的消费倾向也在降低。一方面,一部分高收入者的消费结构已发生了变化,向着更高的奢侈品消费行列迈进。富人人数有限,即使有所增长,总量上也不大,但是我国社会的产品结构由于要满足大众的需要,不可能满足其少部分人的需求,因此其消费难以增长过多,消费倾向呈现下降趋势。另一方面,由于种种原因,中低收入者的预防动机上升,这就进一步降低了社会平均的消费倾向,从而降低整个社会的消费量。 本文通过实证研究来考察城镇收入差距、农村收入差距、城乡收入差距等对消费的影响,数据区间选择1979至2016年,消费、国民收入的数据来自CEIC数据库,城镇基尼系数、农村基尼系数等数据来自Chen et al.(2010)[13]和胡志军 等(2016)[7],城乡收入差距的数据来自中国居民收入分配2016年年度报告。表10给出了主要变量的描述性统计。 表10 主要变量的描述性统计 数据来源:CEIC数据库、中国居民收入分配2016年年度报告。 为了考察变量之间的长期均衡关系,本研究采用协整方法来探讨城镇收入差距、农村收入差距等对消费的影响。建立如下实证模型: lnCt=a0+a1m+a2n+a3gapt+εt 其中:a1、a2、a3分别是参数m、参数n、城乡收入差距gapt等影响消费的程度。 本文的实证研究采取自回归分布滞后的协整方法(ARDL cointegration approach)。传统标准的协整检验主要有基于残差的(Johansen,1988[14];Johansen,1991[15])、基于最大似然方法的(Johansen et al.1990[16])协整检验,但是这些方法往往面临稳健性和序列稳定性问题。和传统的协整研究方法相比较,自回归分布滞后协整方法(Pesaran et al.1997[17];Pesaran et al.1999[18];Pesaran et al.2001[19])的优点主要体现在以下几个方面:一是适合小样本分析,能够得到更稳健的结果;二是模型并不要求同阶单整,估计都是无偏的和有效的,变量或者是I(0),或者是I(1),或者兼而有之,但是不能够是I(2)或更高的单整阶数;三是考虑到模型的内生性问题,即使回归变量是内生的,长期模型系数也是无偏估计;四是ARDL模型能够融入更多的变量。这种方法能够同时研究变量之间的短期和长期关系。ARDL模型是一个动态设定,用因变量的滞后项和自变量的当期或滞后期来解释因变量,短期效应能够被直接估计,长期均衡关系能够被间接估计。针对上述模型,可以建立下列计量模型: 模型通过单一的F检验来判断变量是否存在协整关系,如果通过F检验,则λ1、λ2、λ3都是显著的,变量之间存在协整关系。Pesaran et al.(2001)[19]获得了F检验两个渐进的关键值,一个是上限值,一个是下限值。如果所有序列都是I(0),用下限值来检验长期稳定的关系,其他情况都用上限值来检验协整关系。如果F统计量比上限值大,则存在长期的协整关系;如果F统计量小于下限值,则没有协整关系;如果F统计量在下限值和上限值之间,则不能够确定协整关系。 这种方法通过模型中滞后水平变量联合检验的显著性来判断是否存在长期稳定的协整关系,如果所有的短期项都等于零,则存在长期的协整关系。还可以通过构建误差项,来判断变量是否向均衡回归,如果误差项的系数符号是负的,并且显著,则变量向均衡回归,误差修正项系数的大小反映了向均衡回归的速度。 1.单位根检验 在进行ARDL协整检验之前,要检验序列的平稳性,以保证变量单整的阶数不会大于1,即不要出现I(2)过程,如果出现I(2),则会产生伪回归。首先本文对序列进行单位根ADF和PP检验。本文采用Eviews 9.0软件进行检验,单位根检验的结果如下(见表11): 表11 单位根检验结果 数据来源:作者通过Eviews 9.0软件进行检验而得。 注:(c,t,m)表示单位根检验方程中是否含有常数项、趋势项和滞后阶数(或Newey-West带宽)。ADF检验的最优滞后阶数根据AIC信息准则选择,带宽根据NW Bartlett Kernel选择,* * *(**,*)分别表示在1%(5%,10%)的水平下显著。 如果原序列在5%的显著性水平下不能够拒绝单位根假设,可以认为是非平稳的序列。mt、nt原序列是不平稳的,其一阶差分序列在5%显著水平下拒绝单位根假设,该序列是一阶单整序列,而一阶差分检验都是平稳的。Ct、gapt的ADF检验是平稳的,PP检验是不平稳的,但是一阶差分都是平稳的。 2.ARDL协整检验 在进行边限协整检验前要建立形式如同式(7)的误差修正模型,边限协整检验就是对滞后解释变量Ct、mt、nt和gapt的系数进行联合显著性检验。ARDL模型中最大滞后阶数取5阶。F统计量用于检验原假设:所有水平变量的系数为零(即水平变量之间不存在长期关系),记作F(Ct|mt、nt、gapt),此时对Ct、mt、nt和gapt的系数联合显著性检验结果为: F统计量=29.6307(p=0.010),根据概率水平可知,在95%的置信水平,不能拒绝Ct、mt、nt和gapt之间没有长期关系的原假设,F检验结果显示在5%的显著性水平下拒绝不存在协整关系的零假设,所以Ct、mt、nt和gapt之间存在长期协整关系。 下面利用ARDL-cointegration估计模型。根据AIC准则与SBC准则可知,用AIC准则选择的模型ARDL(5,1,3,5)和用SBC准则选择的模型ARDL(5,1,3,5)一样,ARDL(5,1,3,5)模型的具体参数估计如表12。 表12 ARDL(5,1,3,5)模型的具体参数估计 数据来源:作者根据实证研究结果整理而得。 最后是模型的诊断检验和稳定性检验,可以用拉格朗日乘数检验自相关,用reset检验函数的形式,以及检验残差的正态性和异方差来进行诊断检验,用CUSUM和CUSUM平方检验模型的结构稳定性,如果残差全部在置信区间内,则说明系数是稳定的。除了自相关外,检验结果显示ARDL模型通过了所有的相关诊断检验,没有异方差,残差服从正态分布,模型设定合理,该模型的诊断结果如表13。 表13 ARDL(5,1,3,5)模型的误差诊断模型的诊断检验 数据来源:作者根据实证研究结果整理而得。 可见估计的ARDL模型在5%的显著性水平下通过了相关检验,该模型是合理的。 图5 ARDL(5,1,3,5)模型的CUSUM和CUSUMSQ图 由图5递归残差累积图和平方累积图可以判断,模型估计的系数在样本区内,在5%的显著性水平下基本上也是稳定的。 3.误差修正模型和长期协整关系 进一步可以得到误差修正模型,见表14。 表14 ARDL(5,1,3,5)模型的误差修正模型 数据来源:作者根据实证研究结果整理而得。 由误差修正模型能够看出,短期内,不同的滞后期对消费影响的大小和方向往往差异较大,农村收入差距对当期消费有显著正的影响。一方面,农村收入差距上升,消费上升,这可能由于短期内农村低收入群体的边际消费倾向是上升的,而不是下降的缘故;另一方面,城镇收入差距上升,消费下降,城镇收入差距滞后1期、2期上升对消费有显著负的影响。城乡收入差距对当期消费有负的影响,滞后2、3期城乡收入差距对消费有显著正的影响,滞后1、4期城乡收入差距对消费有显著负的影响。误差修正项ECM的系数为-0.79748,统计上高度显著,并且有正确的符号(负号),误差修正项系数表明经济受到冲击以后,以79.7%速度向均衡恢复。 同样可以得到长期均衡的系数如表15。 表15 ARDL(5,1,3,5)模型的长期系数 数据来源:作者根据实证研究结果整理而得。 注:模型因变量是C。 按估计的长期关系系数,得到如下的消费函数: Ct=0.16605mt+0.32001nt-0.035351gapt+0.14182inpt-0.049476D2008 (8) 由方程(8)可知,模型长期关系系数都是显著的,城镇收入差距和农村收入差距对消费的影响为正,城乡收入差距对消费的影响为负,nt和gapt的系数符号和前面理论的分析完全一致,理论符号符合预期。但农村收入差距增加对消费的影响为正,与前面理论分析不一致。 假定把低收入群体分为较低低收入群体和相对较高低收入群体,较低低收入群体边际消费倾向b1(y3-c3),这里的b1>0,假定较低低收入群体的边际消费倾向是递增的;较高低收入群体的边际消费倾向是(1-b2(y4-c4)),这里的b2>0,假定较高低收入群体的边际消费倾向是递减的。假定其他条件不变,因此低收入群体总的消费为: C1=c3+y4+[b1(y3-c3)2-b2(y4-c4)2],其中: 对m求导: 传统的研究主要是根据收入的变动,测算一国或地区的基尼系数,来反映不同收入群体的收入差距,而本研究根据三角函数图形的特点,构建了三角函数形式的洛伦茨曲线来反映不同群体收入差距的变化。研究结果显示,三角函数的洛伦茨曲线能够很好地拟合中国、美国的收入差距,洛伦茨曲线和基尼系数能够很好地反映不同群体之间的收入差距。进一步地,本文根据三角函数的洛伦茨曲线,计算了相应的基尼系数。为了考察低收入群体和高收入群体的基尼系数,通过极限方法进一步计算出低收入群体和高收入群体的近似基尼系数、收入弹性等。应该说,根据低收入群体和高收入群体的基尼系数,通过基尼系数线性化,能够测算出相应的参数和收入弹性,尽管只是近似值,但是基本能够反映收入差距的变动。最后本研究构建了理论模型,进一步考察收入差距对居民消费的影响,得到的结论为:居民收入差距越大,总消费是下降的,居民收入差距越小,总消费是上升的。研究发现:低收入群体之间的收入差距越大,消费是下降的;高收入群体之间的收入差距越大,消费也是下降的。实证结果显示高收入群体之间的收入差距越大,消费是下降的;低收入群体之间的收入差距越大,消费是上升的,分析认为这主要是由于边际消费倾向决定的。扩内需,尤其是扩消费是我国宏观经济政策的重要目标,因此缩小收入差距,特别是提高中低收入群体的收入有利于我国消费内需的增加。 根据以上分析,随着收入差距的扩大,总消费是下降的,这同时还意味着居民储蓄是上升的。从我国的实际情况来看,2015年底,我国居民储蓄存款余额是5年前的2.28倍,是10年前的将近5倍,更是20年前的9倍之多。与此同时,我国居民储蓄存款余额占GDP的比重从1978年的5.72%迅猛地提高到2016年的81.5%。我国居民储蓄存款所呈现的这种“高增长”与“高储蓄”态势,和消费增长缓慢相对应,因此缩小收入差距,扩消费仍然是今后的一项重要任务。 注释: ①如果所有收入都集中在一人手中,而其余人口均一无所获时,收入分配达到完全不平等,洛伦茨曲线成为折线。另一方面,若任一人口百分比均等于其收入百分比,从而人口累计百分比等于收入累计百分比,则收入分配是完全平等的,洛伦茨曲线成为通过原点的45度线。 ②基尼系数(Gini Coefficient)是意大利经济学家基尼(Corrado Gini,1884—1965)于1912年提出的,是国际上用来综合定量考察居民内部收入分配差异状况的一个重要指标。基尼系数最大为“1”,最小等于“0”。前者表示居民之间的收入分配绝对不平均,即100%的收入被一个单位的人全部占有了;而后者则表示居民之间的收入分配绝对平均,即人与人之间收入完全平等。但这两种情况只是在理论上的绝对化形式,在实际生活中一般不会出现。因此,基尼系数的实际数值只能介于0~1之间。 ③洛伦茨曲线用以比较和分析一个国家在不同时代或者不同国家在同一时代的财富不平等,该曲线作为一个总结收入和财富分配信息的便利的方法得到广泛应用。 ④考虑到函数的可积性,前面乘以xm-1。 ⑤数据主要来自OECD数据库。由于方法和数据来源的不同,国内计算基尼系数的结果往往差异较大,因此本文采用洛伦茨曲线拟合的数据来自OECD数据库,它提供了不同人口比例的收入占比。本文采用了OECD数据库所能提供的某几年的数据。 ⑥实际上,根据基尼系数的线性近似,可以计算出m和收入弹性的近似值,这个近似值是在低收入群体附近线性展开的。虽然并不十分精确,但可以反映其变动趋势。 ⑦根据基尼系数的线性近似,可以计算出n和收入弹性的近似值,这个近似值是在高收入群体附近线性展开的。离高收入群体越近,n的估值和收入弹性越准确。 ⑧受篇幅限制,本文不再给出详细的推导过程,如需要,可向作者索取。 ⑨同⑧。
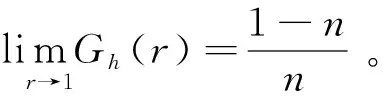
(三)混合洛伦茨曲线的非线性拟合与函数参数的计算


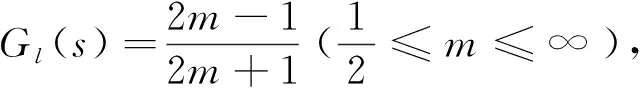
(四)构建基于混合洛伦茨曲线的收入差距与消费的理论模型
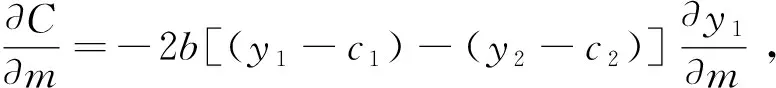



四、实证研究
(一)数据来源及描述性统计

(二)实证模型及实证方法






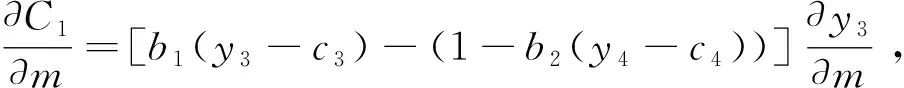

五、研究结论与建议

