基于截断高斯分布的异质自行车离散模型

尹德鹏，成卫，雷建明

(1. 昆明理工大学 交通工程学院，云南 昆明 650500；2. 玉溪市公安局 交通警察支队，云南 玉溪 653100)

城市自行车数量的飞速增长和不合理、不完善的管控措施导致自行车成为影响城市交通的重要因素之一。为此，在中国的很多地区设置了自行车专用车道，并对其进行了信号管控。对自行车流离散特性进行分析是实现自行车信号控制、自行车微观交通仿真和自行车到达流量预测的基础。由于行驶过程中自行车的车型特征和能源供给的差异，再加上骑行过程中骑行者的驾驶行为和期望速度不同，使得自行车在路段上出现车流的“离散现象”[1]。

近年来，自行车交通流特性已成为学者们的研究热点。王丹[2]根据实测数据，对自行车的时空分布特性和速度特征进行了分析，并建立了自行车交通流模型，但该研究仅以电动自行车为主。周旦[3]利用Logistic方法，分析了2种自行车的交通流特性，并建立了混合自行车交通流模型。该模型能够较好地描述混合自行车在不同状态下的变化特征，但并未考虑车道宽度对模型的影响。南天伟[4]等人利用元胞自动机模型，分析了自行车中电动自行车与传统自行车的车辆构成比例对交通流三参数关系的影响，并建立了混合自行车流模型。李黎山[5]等人考虑自行车的异质特性，从空间比和感知密度出发，结合元胞传输模型，建立了自行车交通波计算模型。在车流离散特性方面，于泉[6]等人对车队离散模型统计时间进行了研究。他发现6～10 s为最佳统计时间。李瑞敏[7]等人利用回归分析方法，考虑4个时段的车流分布，对城市交通流离散模型进行了优化。姚志洪[8-9]等人以Robertson模型为基础，提出公交车与小汽车的异质交通流离散模型，但却忽略了不同交通流之间的相互干扰。巫威眺[10-11]等人根据车辆行程车速和行程时间的有界性，建立速度服从截断正态分布的车队离散模型，提高了Pacey模型的实用性。杨文武[12]等人根据车队离散模型，对下游交叉口到流率进行了预测，为交叉口信号协调控制提供了依据，使信号配时方案更加合理化。这些成果仅针对混合自行车与车队离散的研究，多数在同质交通流的基础上展开，并未考虑自行车流的异质性；此外，关于车队离散特性的研究集中于城市机动车离散特性和相关参数的校正，并未对自行车的离散特性进行深入研究。因此，本研究将以 Robertson离散模型为基础，建立行程时间服从截断高斯分布的城市自行车异质车流离散模型，计算下游路段自行车到达流量分布与上游自行车流量离去模式的定量关系，以期为城市自行车专用车道信号协调控制和自行车微观交通仿真与交通流预测提供理论依据。

1 数据获取与分布假设拟合

1.1 行程时间分布的假设

在自行车异质交通流中，由于传统自行车与电动自行车的车辆特性和行驶速度存在着差异，使得这2种自行车的行程时间也存在着很大的差异。根据交通流的可叠加性[13-14]，可将传统自行车和电动自行车看成两股不同的车流，分别建立离散模型，然后，将二者叠加，可获得异质自行车交通流离散模型。在实际行驶过程中，自行车行程时间在最大行程时间与最小行程时间之间的有界区间内。在模型建立之前，首先假设传统自行车和电动自行车的行程时间均服从截断高斯分布。

假设：传统自行车行程时间 tb服从区间为的高斯分布，参数为将之记为电动自行车行程时间 te服从区间为[的高斯分布，参数为

根据高斯分布的可叠加性，异质自行车行程时间 t也服从截断高斯分布，即 t:(μ, σ2), tmin≤t≤tmax。

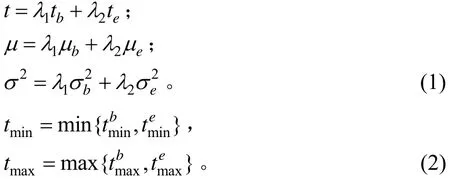
式中：λi为第 i股车流的车辆比例系数；σ,σb和 σe分别为混合自行车行程时间、传统自行车行程时间和电动自行车行程时间标准差；μ, μb和μe分别为混合自行车行程时间、传统自行车行程时间和电动自行车行程时间均值分别为混合自行车行程时间、传统自行车行程时间和电动自行车行程时间的最小值；be分别为混合自行车行程时间、传统自行车行程时间和电动自行车行程时间的最大值。

假设自行车行程时间t服从截断高斯分布，其分布函数为F(t)，概率密度函数为:

式中：a为截断分布系数，保证概率密度为1；n为自行车异质车流中的交通流股数(本研究将自行车看作传统自行车与电动自行车组成的交通流，取n=2)。

其分布函数为：

根据分布函数的基本性质，有F(tmax)=1，则a[F(tmax)]-F(tmin)=1，从而得到分布系数为：

t（:，将式中正态变量进行转换，将式(6)转化为标准正态分布：

式(7)中的相关参数可根据实际调查数据计算得到。然后，根据实测数据进行拟合，观测行程时间是否服从截断高斯分布。

1.2 数据的获取

为了验证假设是否成立，对昆明市主城区环城北路中北京路至万华路路段的自行车交通数据进行了实地调查。该路段长622 m，调查路段为自行车流量较大且具有物理隔离的自行车专用车道。该路段干扰系数小，路面平整，行车视距良好，视频录制范围广。选择良好天气进行数据观测。调查路段上游为信号控制交叉口，拍摄点位分布如图1所示。考虑自行车到达下游交叉口位置时会出现排队现象，为数据统计方便，将断面C位置放在距离下游断面50 m的位置。

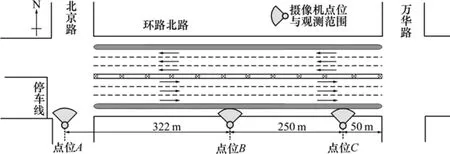
图1 调查路段拍摄点位分布Fig. 1 The distribution of road section shooting points

根据调查数据特征，将调查时间分为平峰和高峰2个时段(平峰15:00—16:00，高峰17:30—18:30)。分别调查了 12个信号周期的自行车交通数据，从各断面视频录像中获取自行车流量和行程时间数据(其中：平峰时段，自行车数据1 795条；高峰时段，自行车数据2 462条)。数据统计结果见表1。

表1 调查统计数据Table 1 The data of survey statistics

从表1中可以看出，高峰时段的车流远大于低峰时段的。数据具有明显的高峰和平峰特征，不同时段传统自行车所占比例也不相同，最高比例达13.82%。2种自行车流在该路段的平均行程时间存在着较大的差异，但两者的行程时间都在最大、最小行程时间的范围内，具有明显的有界性。

1.3 假设的拟合

根据调查数据，对行程时间分布的假设进行了验证。对平峰时段和高峰时段的行程时间拟合参数进行了计算，参数估计值见表 2。根据拟合参数估计，对平峰和高峰时段的行程时间进行了截断高斯分布拟合，拟合效果如图2所示。

从图2中可以看出，传统自行车与电动自行车行程时间特征的差异较大。电动自行车行程时间小且标准差也较小；而传统自行车行程时间较大，且标准差也较大。表明：传统自行车的速度比电动自行车的速度慢，2个时段的行程时间分布均呈双峰型。从表2中还可以看出，截断高斯分布拟合效果良好，混合自行车2个时段的决定系数R2在0.89以上，拟合效果较好。表明：本研究假设自行车行程时间服从截断高斯分布是合理的。

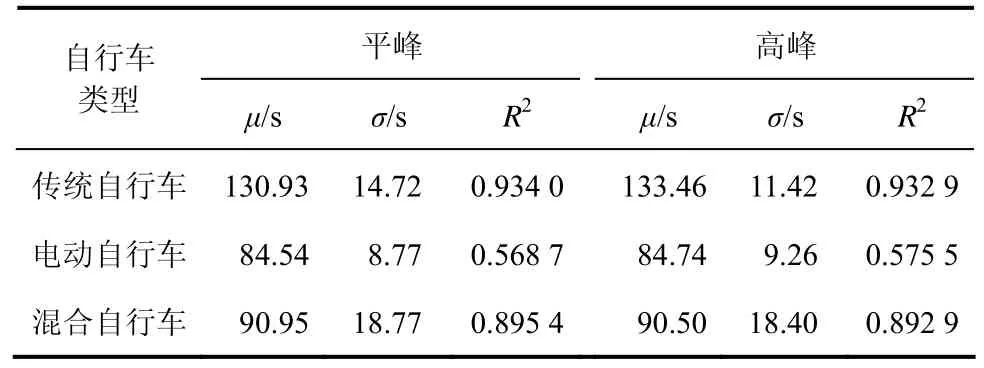
表2 分布曲线拟合参数估计值Table 2 Estimated values of fitting parameters from the distribution curve

图2 行程时间分布的拟合效果Fig. 2 The fitting effect of travel time distribution

2 自行车离散模型的建立

假设调查时段内从上游断面(即x=0)驶出的自行车流量是qA(t0)，那么统计时间间隔Δt内从上游停止线驶出的自行车数量是qA(t0)·Δt。如果该部分自行车从上游交叉口到达下游某断面的行程时间为T，那么这些自行车将在[t0+T,t0+T+Δt]时间内到达下游断面。时间t到达下游断面的自行车流率为：

式中：qC(t)为下游交叉口时间t的流率；T1和T2分别为到达下游交叉口车辆的可能最小和最大行程时间。

绿灯启亮后，调查数据统计时间以3 s为单位，得到上游断面自行车流量的离去模式，如图3所示。

图3 上游交叉口流量的离去模式(斜线型)Fig. 3 Departure mode of the upstream intersection flow(slash type)

自行车离去规律为斜线型，则上游自行车离去流率为：

式中：Q为绿灯时间从上游离去的自行车流率；b为单位时间间隔自行车流率的折减系数；tg为绿灯启亮后自行车放行时间；tG为有效绿灯时间。

自行车流量离去为斜线型，其决定系数R2为0.804 3，折减系数b为0.614 7。

2.1 到达流率模型的推导

1) 当tmax≤tmin+tg时，

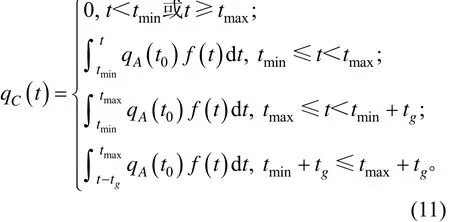
2) 当 tmax＞tmin+tg时，

2.2 截断高斯分布的到达流率模型的推导

截断高斯分布的概率密度函数为：

将其代入式(11)，(12)中，得到下游断面时间t的到达流率分布模式为：

1) 当 tmax≤tmin+tg时，

3 实例分析

3.1 上游流量离去分布模式的分析

调查路段上游为信号控制交叉口。根据各断面拍摄的视频数据，横坐标是以3 s为单位的统计时间数，纵坐标是3 s统计时间内通过该断面的自行车数量，给出的单个信号周期内各断面自行车离散分布如图4所示。

从图4中可以看出，自行车在路段行驶的过程中发生明显的离散现象。当自行车到达下游断面时，离散分布逐渐趋于平稳。

3.2 下游断面到达流率的预测

根据建立的自行车行程时间分布函数和上游交叉口离去的自行车流率分布模式，利用数据分析软件，计算下游自行车到达流率分布。将最终计算结果与实际测量数据进行了对比。平峰时段和高峰时段下游断面C处的自行车到达流率分布如图5所示。本试验模型与Robertson模型均方误差见表3。

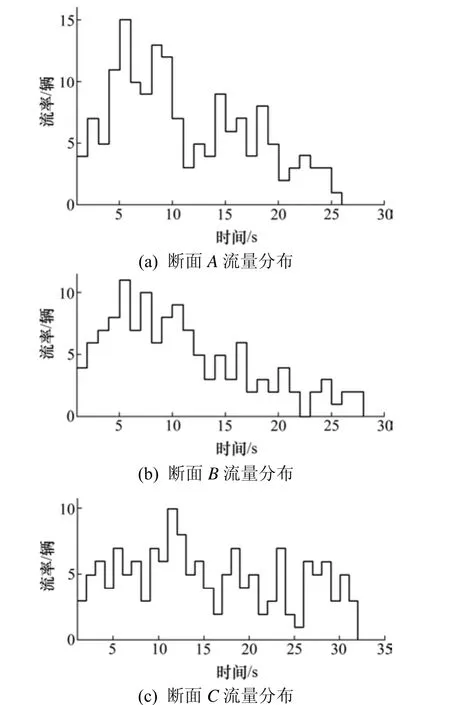
图4 调查路段各断面流量分布Fig. 4 Diagram of flow distribution of each section in the investigated road

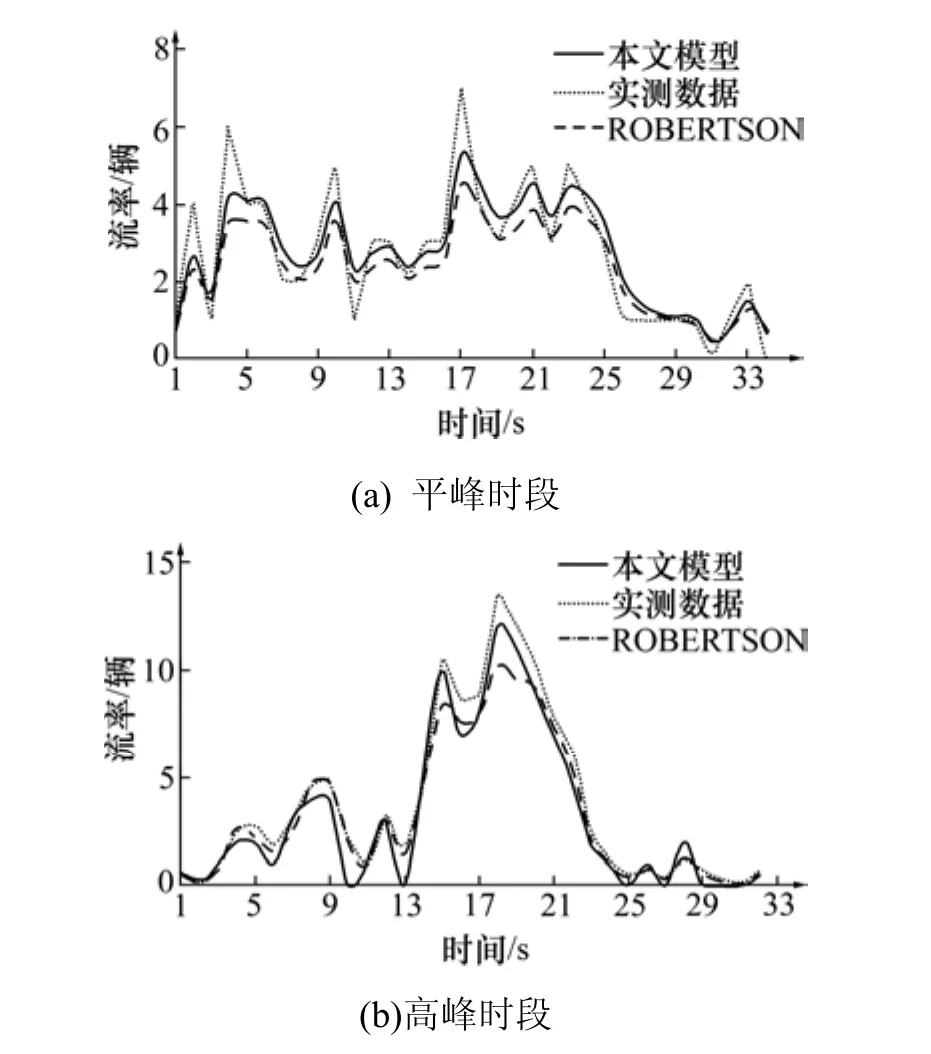
图5 下游到达流率预测分布Fig. 5 Prediction distribution of the downstream arrival flow rate

表3 模型误差分析Table 3 The mean square error of the model

从图5和表3中可以看出，本模型与实测数据相对误差最大为平峰1.813 5辆自行车、高峰2.011 8辆自行车，平均相对误差均小于1辆自行车，预测结果误差在可接受范围内。且本模型与 Robertson模型相比，其均方误差降低了22.53%。表明：基于截断高斯分布的离散模型能够更好地描述异质交通流条件下的自行车离散规律；Robertson模型假设行程时间服从几何分布，并未考虑异质交通流条件下自行车中传统自行车与电动自行车行程时间的差异性，因此，其预测误差比本模型的预测误差大。

4 结论

在 Robertson模型的基础上，考虑城市自行车行程时间的有界性，利用截断高斯分布拟合自行车行程时间，发现异质车流条件下自行车行程时间呈双峰型，且截断高斯分布能够较好地拟合行程时间分布，并基于此处构建了服从截断高斯分布的城市自行车异质交通流离散模型。最后，将本模型和Robertson模型的计算结果与实际调查数据进行了对比分析，发现本模型的平均均方误差比同质流条件下Robertson模型的提高了22.53%，其平均相对误差均小于1辆自行车。

但由于数据采集是在低干扰条件下同一条路段上的自行车交通数据，忽略了其他交通流的干扰和不同宽度的自行车道对离散特征的影响。后续研究可在本研究的基础上考虑其他交通流的干扰，同时，研究不同车道宽度条件下的车流离散模型。