考虑司乘人员工作时间窗的高铁快巴车辆调度与人员排班综合优化

李凯明，宋瑞，郭小乐

(北京交通大学 综合交通运输大数据应用技术交通运输行业重点实验室，北京 100044)

为建设“公交都市”、满足居民日益多样化的出行需求，解决常规公交在高峰期或地铁停运期间运力不足的问题，北京公交集团开通了新型公交服务产品——高铁快巴。高铁快巴原计划根据高铁旅客到京情况进行线路、发车时刻的调整，因此其调度、排班方案等相比传统公交更加灵活，也联系得更加紧密，牵一发而动全身。但由于缺乏理论指导，目前高铁快巴仍使用传统运营模式，即采用固定间隔30 min发车、单线路调度的模式，导致乘客体验差、企业成本高，如2018年春节期间开通的两条高铁快巴春运专线发车近6000次，但上座率却不到20%。不当的运营模式所导致的空车率高等问题显而易见，而司乘人员也有反映工作时间较长等问题。因此有必要针对高铁快巴的车辆调度与人员排班优化问题进行研究。

公共交通系统优化包括线网、时刻表、车辆调度、人员排班优化4个环节，研究者通常依次对各个环节进行优化[1-3]。由于每个环节相互紧密关联，依次对各个环节进行优化可能导致仅出现局部最优解[4]，而综合优化能够统筹考虑各个环节，因此近年来同时考虑两个甚至更多环节的综合优化逐渐受到更多的学者关注。

Prileszky等[5]分析了车辆调度与人员排班问题的综合优化方法和序贯法的主要步骤和面临的问题，并提出了一种交互式优化方法，该方法能提高手工作业的效率。Lam等[6]提出了考虑司机之间可以互相交换车辆的约束模型，将该方法与序贯法进行对比，发现其优化效果更好。Dominguez-Martin等[7]利用车辆路径模型构建调度与排班综合优化模型并通过分支定界法求解不等式。de Athayde Prata[8]将调度和排班综合优化看作多商品的最大覆盖问题，在此基础上建立多目标优化模型，并采用PESA-II算法进行求解。文献[9-10]为多车场的整体优化提出了基于列生成和拉格朗日启发式算法两种模型。Mesquita等[11-12]基于多商品网络流模型和集划分/覆盖模型建立了调度与排班综合优化的整数线性规划模型，分别运用了精确、启发式以及模糊的分支定界法对其进行求解。de Groot等[13]通过将多车场的大型问题进行分割，分别对每部分进行整体优化，能够有效节省计算时间。而Haase等[14]创造性地从司乘人员的网络结构出发(绝大多数研究都是从车辆的网络结构出发)，构建单车场-同种车型的集覆盖模型，而后使用列生成算法混合分支定界法求解。

以上研究主要探讨了车辆调度与人员排班的综合优化问题，但建立的模型均默认司乘人员可以执行一天内所有的车次，缺少对司乘人员工作时间安排的考虑。如司乘人员实际排班的班次通常都有相应的工作时间要求(即司乘人员的工作时间窗要求)，包括单班与整班，整班又包括早班和晚班[15]。而高铁快巴运营的灵活性也导致车辆在途时间相对多变，对人员排班提出了更高的要求，因此有必要考虑司乘人员工作时间窗的高铁快巴车辆调度与人员排班问题，在保证完成班次任务的前提下，尽可能考虑司乘人员的时间需求，促进多样化公交服务规范化运营，从而更好地满足乘客多样性需求，提高城市公交服务水平，提升公共交通的公众吸引力。

基于此，本文针对高铁快巴的车辆调度与人员排班综合优化问题(integrating vehicle scheduling problem and driver scheduling problem，VDSP)进行研究，引入司乘人员的工作时间窗，并提出了相应的综合优化模型，最后利用分支定界法求解算例,说明了模型的正确性与有效性。

2 模型建立

2.1 问题描述与假设

本文所研究的问题属于典型的VDSP问题，是车辆调度问题(vehicle scheduling problem，VSP)与人员排班问题(driver scheduling problem，DSP)的结合，研究中通常使用集分割/覆盖模型(set-partitioning/covering formulation)对其进行建模。可以将其详细描述为：某城市公交车场站集合为D，则某公交场站d∈D，在已知其司乘人员集合s∈S以及其高铁快巴线路的正常运营车辆班次(以下简称车次)数量及其起始站点、到发站时刻的情况下，建立时空网络Gd=(Nd,Ad)(其中，Nd代表公交场站d的车辆到发时刻，Ad代表Nd之间的车辆运行行为)，求解设计高铁快巴车次以及司乘人员任务m∈Md(i,j)的最优方案，其中，Md(i,j)为以起始站点的发车时刻升序排列的司乘人员班次任务集合。

为简化问题，做以下假设：

(1)车次(包括正常运营车次、空驶车次和原地等待)以起始站点的发车时刻的时间数列升序排列，若发车时刻相同则按照到达时刻升序排列，与司乘人员班次任务一一对应；

(2)所有车辆与司乘人员班次任务所需成本已经确定；

(3)不考虑场站的公交车辆限制；

(4)在时空网络构建中，若某一车次与间隔最近的车次满足空驶时间条件，则两个车次之间插入可能的空驶车次；若两个车次时间间隔较大(超过两倍站点返回场站的时间)，则中间不插入原地等待或空驶车次，车辆插入可能的返回场站车次；

(6)司乘人员的相邻工作班次任务间隔必须满足最小停留时间；

(7)司乘人员可以在首末站点以及场站进行工作交接；

(8)司乘人员对工作时间均有不同要求，执行班次需满足时间窗约束(即各司乘人员工作时间的上下限约束)，需满足最大工作时间要求。

2.2 目标函数

车辆调度与人员排班综合优化的目标是最小化公交企业的运营成本。而运营成本C总分为车辆运营成本C车辆与司乘人员运营成本C乘务员。

minC总=C车辆+C乘务员。

(1)

(1)司乘人员运营成本

司乘人员运营成本C乘务员为所有场站所有执行的司乘人员班次任务与对应的班次任务运营成本的乘积加上司乘人员更换车辆所带来的额外成本C换。班次任务运营成本由班次任务运营时间与单位时间运营成本的乘积求得。

(2)

(3)

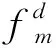
(2)车辆运营成本

车辆运营成本C车辆包括车次执行成本Ce与车辆使用成本Cu。车次执行成本Ce为所有场站所有执行的车次(包括正常运营车次、空驶车次和原地等待)与对应的车次运营成本的乘积，车辆使用成本Cu为使用的总车辆数B与车辆使用费用C使用的乘积，其中C使用中包含了使用车辆就会出现的成本如车辆维护成本、车辆折旧成本等。

(4)

(5)

(6)

综上所述，车辆调度与人员排班综合优化的目标函数如式(7)所示：

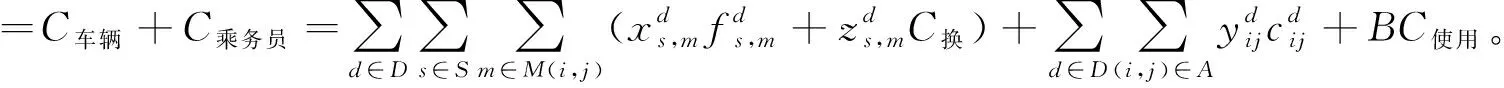
(7)

2.3 约束条件

模型的约束条件如下：

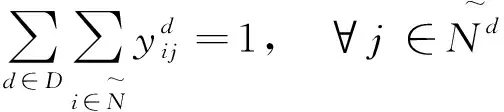
(8)

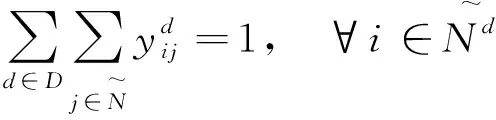
(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

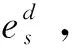
3 算例研究

考虑有3个公交首末站A、B、C以及1个场站D，其中站点A为高铁站，因此仅考虑A—B、A—C之间的上下行公交线路和3个站之间可能的空驶线路，不考虑B和C之间的线路。站点A到站点B的行驶时间为0.7 h；站点A到站点C的行驶时间为1.2 h；站点A到场站D的行驶时间为0.3 h；站点B到站点C的行驶时间为0.5 h；站点B到场站D的行驶时间为0.8 h；站点C到场站D的行驶时间为0.8 h。

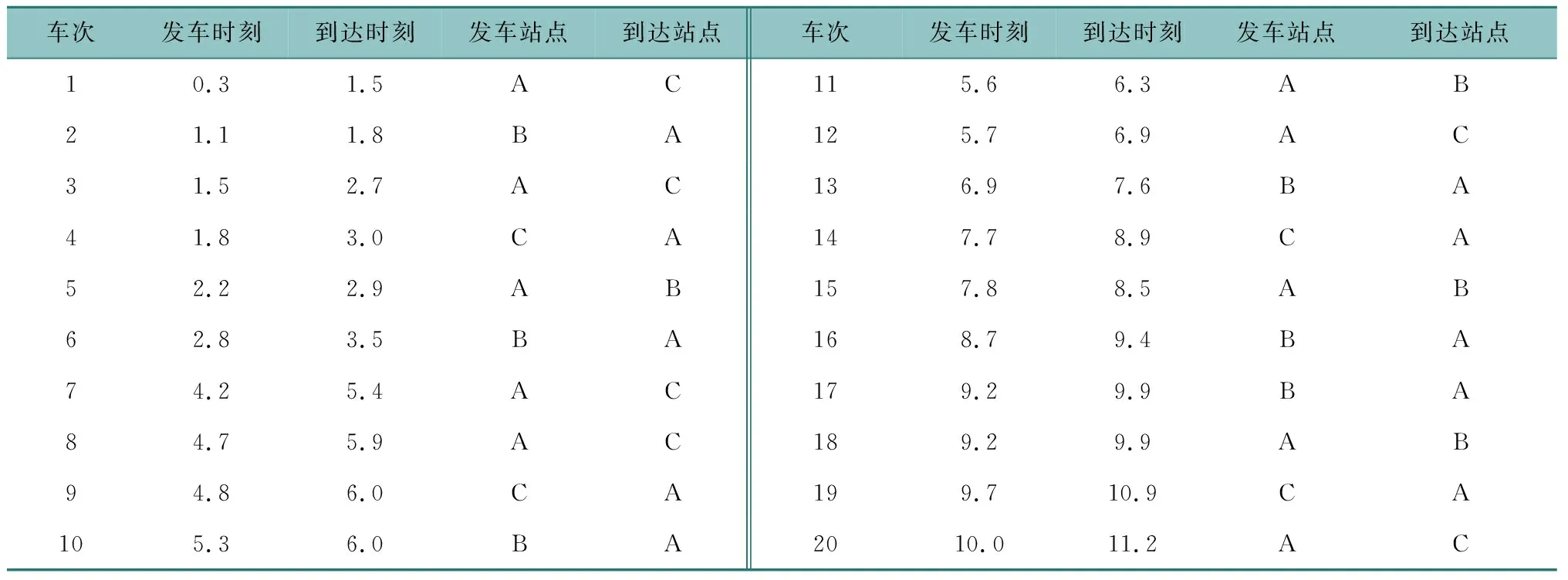
表1 已知时刻表

按照假设插入驶入驶出、空驶、等待等车次，并将所有时空网络点的时间数列升序排列，同时将车次(包括正常运营车次、空驶车次和原地等待)以起始站点的发车时刻的时间数列升序排列，若发车时刻相同则按照到达时刻升序排列。构建时空网络，具体如表2所示。该场站共有8名司乘人员，具体工作时间窗情况如表3所示。

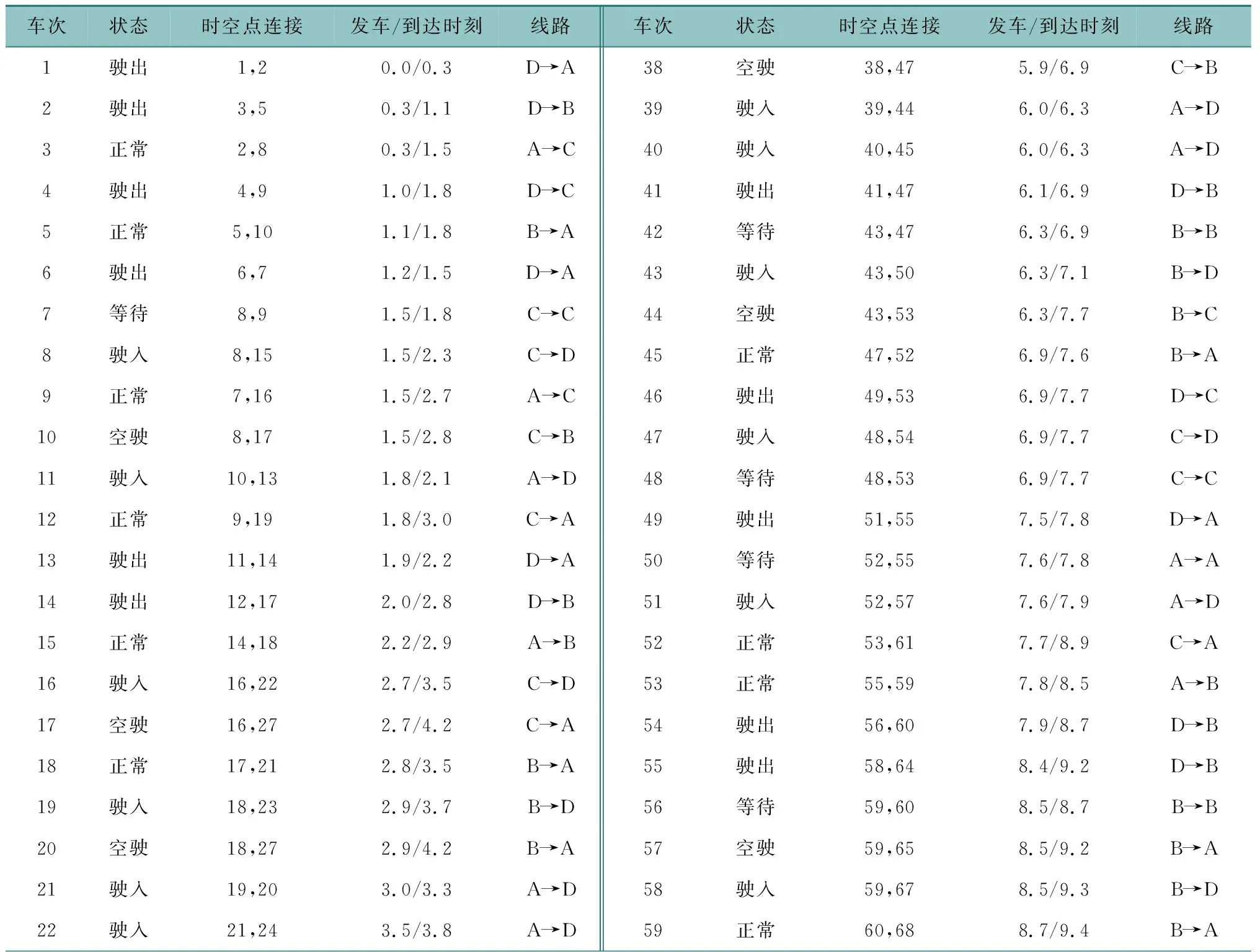
表2 时空网络表

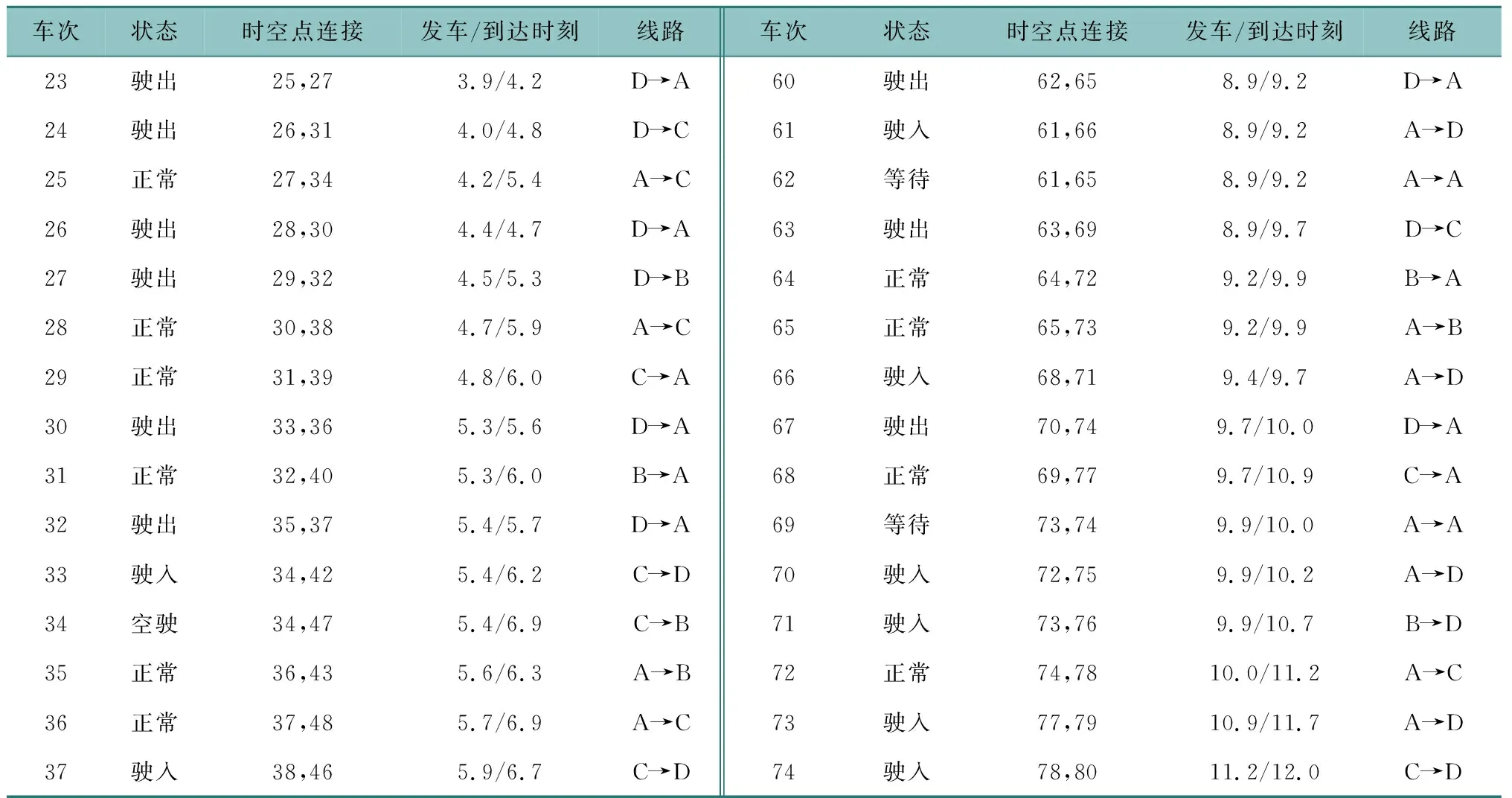
续表2

表3 司乘人员情况

计算时取司乘人员平均行车单位时间成本为2 元/h，平均等待单位时间成本为0.4 元/h[16]；由于司乘人员更换线路带来的隐性成本C换取50元/(人·次)。依照目前高铁快巴运营现状，其车辆核载人数为10人，人均票价为15.32元。高铁快巴预计满载率为50%，平均运营速度为15 km/h，单车运营成本为4.8元/km[17]；参考司乘人员行车成本与等待成本之间的比例，取单车等待成本为正常车次成本的1/5；为尽可能地减少车辆的使用数量，车辆使用费用C使用取尽可能大的值2000元/(车·次)[18]。由此求得单位时间车辆与司乘人员费用如表4所示。

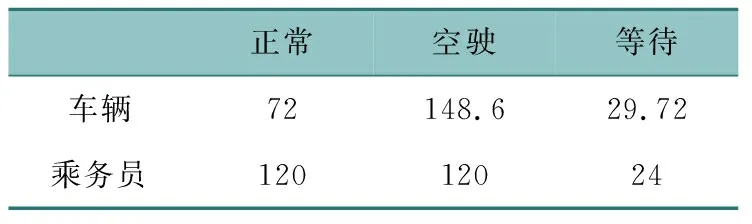
表4 单位时间车辆与司乘人员成本

第2节建立的模型为线性整数规划模型，分支定界法是求解线性整数规划最常用的精确算法。因此使用分支定界法对该模型进行求解，最终得到最优解如表5、表6所示。最优解使用车辆数为6辆，总成本为22 382.79元，其中车辆使用成本为12 000元，正常车次成本3 533.3元，驶入驶出车次成本3 456.88元，空驶车次成本545.26元，等待成本45.048元，司乘人员的成本为2 805.3元。

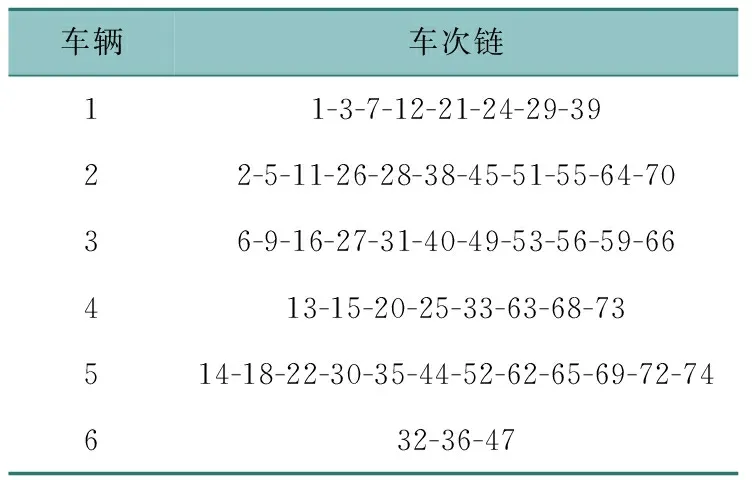
表5 车辆调度方案

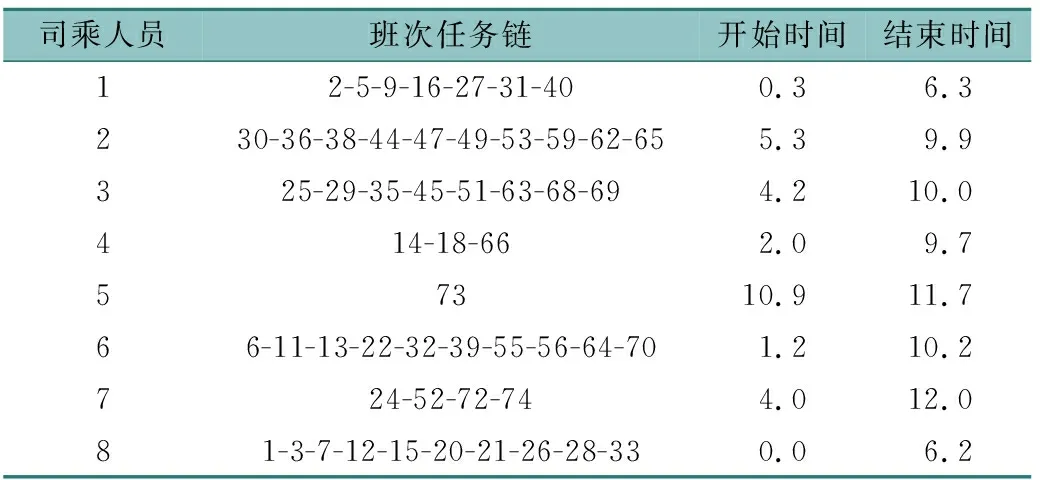
表6 司乘人员排班方案

从表5中可以看到，最终执行的车次有53次，其中正常车次20次，驶入驶出车次26次，空驶车次3次，等待车次4次，这是因为提前设置的参数尽可能地减少了空驶的车次以及驶入驶出的车次。从表6中可以看到，司乘人员执行的任务全部符合其工作时间窗要求以及其接续班次任务的站点需求。由此验证建立的模型能够有效地解决考虑司乘人员工作时间窗的高铁快巴车辆调度与人员排班问题。

为了验证模型的优越性，设计另外两种方案。其中方案A是目前高铁快巴所使用的方案即为单线路调度，车辆调度与人员排班独立进行优化，用以验证本文提出的模型对比现有方案的优越性；方案B为目前一般公交运营时所使用的方案即为多线路调度，车辆调度与人员排班独立进行优化的方案，用以验证综合优化对比独立优化的优越性。具体对比如表7所示。

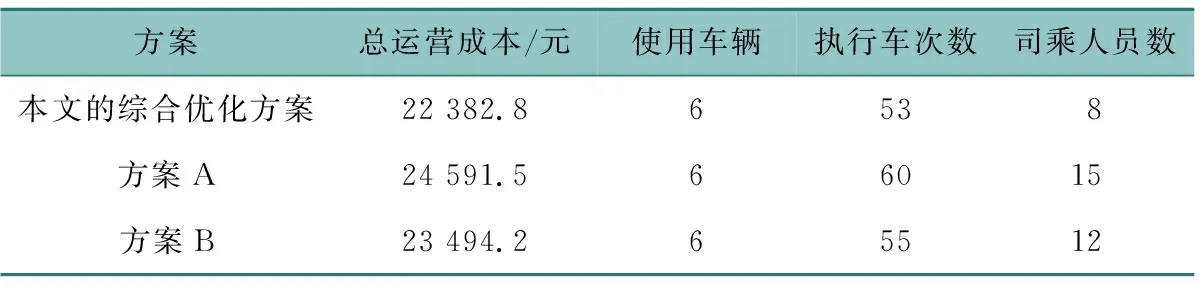
表7 不同方案对比

从表7中可以看出，本文提出的综合优化方案相比于方案A减少2 208.7元，优化率为8.98%；相比于方案B减少1 111.4元，优化率为4.73%。若采取目前高铁快巴的运营方案，需要15个司乘人员才能够满足运营需求且执行车次达到60个，所以总运营成本最高；在独立的对车辆调度与人员排班进行优化后，执行车次减少为55车次，需要12个司乘人员才能够运营；而综合优化方案，执行车次为53车次，司乘人员数也减少为8个人，总运营成本最低。由此可以验证考虑乘务员时间窗的综合优化方案相比于独立的优化方案，在解决高铁快巴的调度与人员排班问题上具有更好的应用效果。

4 结论

针对创新型公交服务产品高铁快巴与常规公交相比在时间上更加灵活的特性，充分考虑司乘人员对工作时间的特殊要求，引入司乘人员时间窗，将车辆调度与人员排班进行综合优化，利用时空网络构建以企业运营成本最小为优化目标的高铁快巴车辆调度与人员排班综合优化模型，最后利用分支定界法计算出最优的车辆调度与人员排班方案，结果表明该模型能够有效解决高铁快巴的车辆调度与人员排班问题,减少司乘人员数量、降低运营成本，从而为公交管理部门、企业提供辅助决策。

但是本文仅使用了企业的运营成本作为目标函数进行优化，缺乏对夜间乘客等待时间成本的考虑。同时在最优化方案中司乘人员的工作量相差较大，如何平衡司乘人员之间的工作量也是下一步的研究方向。