基于Bootstrap的调距桨装置外油管疲劳寿命评估
孙林凯,吕堂祺,朱凌南
(1. 海军驻上海地区第三军事代表室,上海 200031;2. 上海船舶设备研究所,上海 200031)
0 引言
船舶推进装置性能直接影响船舶的操纵性、安全性和任务能力。可调螺距螺旋桨[1],又称为调距桨,可通过桨叶相对于桨毂转动实现螺距调节,从而保证螺旋桨在不同工作条件下具备优良的运行效率、操作性和机动性,目前已广泛应用于各类船舶的主推进装置。而液压系统是整个调距桨装置的关键结构,保证其安全性与可靠性对于实现调距桨的稳定动力输出具有至关重要的作用。外油管作为液压系统动力传输的重要载体,长期面临着低振动、低噪声的使用环境,在实际使用中会发生高周低应力疲劳断裂故障,且多发生于焊接位置处。为了评估油管寿命状态,对比不同焊接工艺和结构的疲劳性能,有必要开展不同载荷下的油管疲劳试验。
由于疲劳寿命试验成本的限制,通过加速寿命试验获得的数据较为有限,在本次试验中的外油管试样数量极少,且寿命分散性较大,难以采用一般小子样寿命评估方法[2]进行评估。本文采用扩展的 Bootstrap方法对调距桨装置外油管进行极小子样疲劳寿命评估,从而解决了在及其有限的试验数据基础上预测了旧油管和新油管的疲劳寿命,为相应油管焊接工艺与结构的改进优化提供重要参考。
1 外油管加速寿命试验
1.1 外油管疲劳试验情况
疲劳试验件一共4件。每根油管在距离铜条端部(长端侧)40 mm处上下对称位置粘贴标定应变片,安装前将应变片读数清零,安装完成后,施加载荷同时监测应变计读数。根据实船测试,确定焊接点的工作应力为58.5 MPa,断裂处的应力值为 66.75 MPa。试验中,以断裂处的应力值66.75 MPa作为疲劳试验的载荷基准。钢管弹性模量按210 GPa计算。试验均采用载荷增量法加载,起步载荷、循环基数、试验增量均有所不同。
1.2 试验数据
本次疲劳试验一共做了4件。因此,本次疲劳寿命评估的可用试验数据为4个,其中从实船上截取的旧油管和新焊接的油管试样的试验件各2件。具体试验结果列于表1。
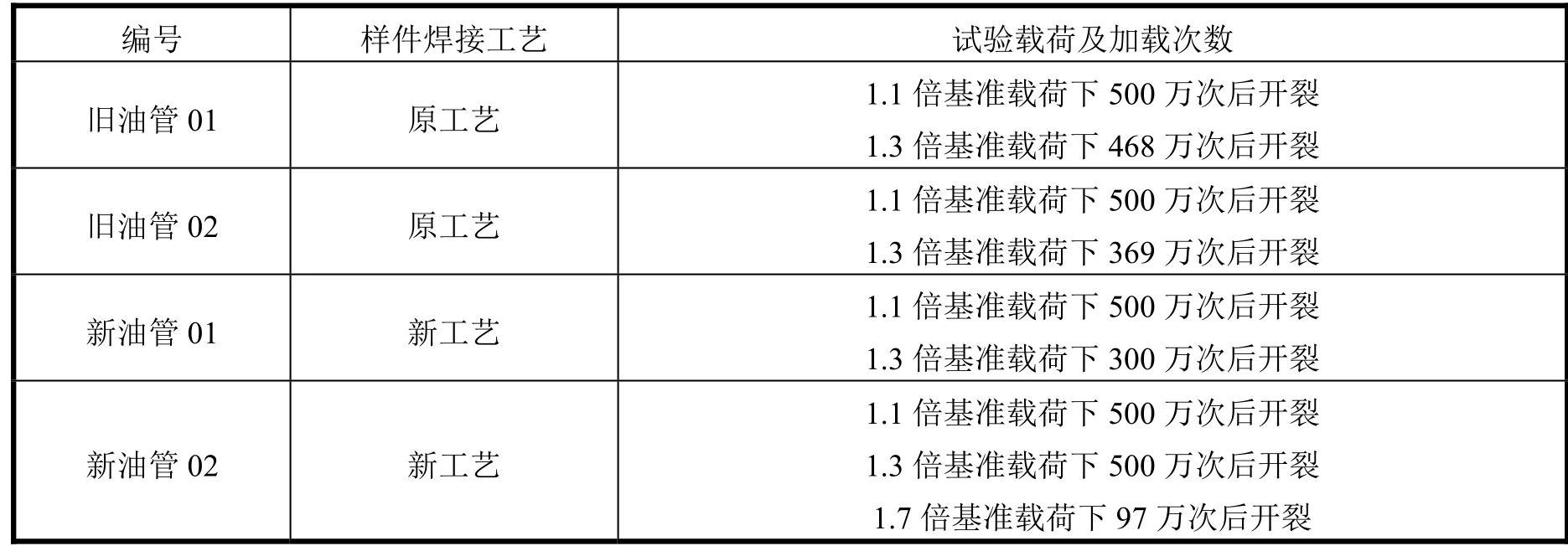
表1 外油管疲劳试验结果及寿命折算
2 加速疲劳试验的折算方法
对于船舶结构而言,结构细节处的塑性影响可以忽略,线性累积损伤理论可以成立。依据加速疲劳寿命的折算方法,给出本次外油管疲劳寿命试验的折算办法[3-4]。
根据S-N曲线和等寿命曲线的直线假设,可得:
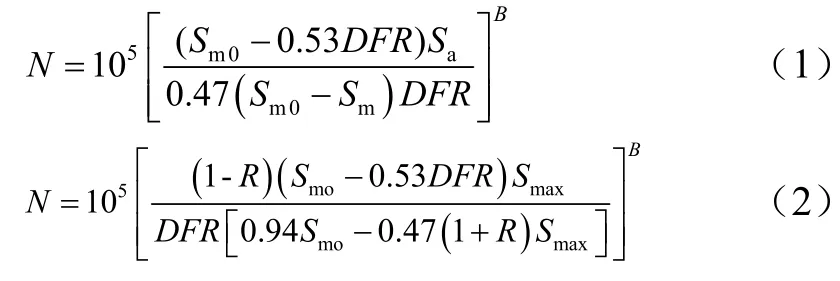
式中:B为S-N曲线斜率;DFR为细节疲劳额定值;R为应力比;Sm为平均应力,MPa;Sa为应力幅;Smax为最大应力,MPa。
通过等损失折算,应力谱可当量成某一级应力和相应的当量循环数。将该级应力选定为R=-1,即Sm=0的应力水平,该级应力水平既有Sm等于常数的S-N曲线的特征,又有R等于常数的S-N曲线的特征。在Sm=0时,Sa=Smax,可得
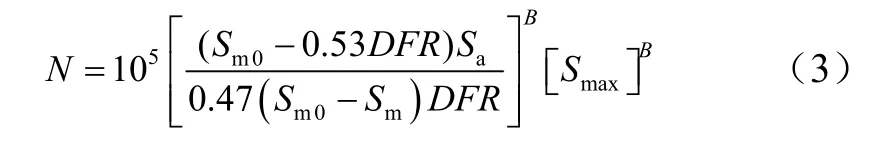
对于细节已确定的结构 DFR值不变,利用S-N曲线的直线假设,根据式(3)可得应力水平对寿命比的影响。

调桨装置的外油管材料为20钢,根据文献[9],可查的B值为-3.92。根据外油管实测载荷、标定载荷(标定点应力水平),给出试验中所有应力水平和载荷折算倍数。并据此将不同应力水平下的外油管寿命均折算为 1.0倍应力水平下的疲劳寿命。
3 极小子样寿命评估
由于旧油管和新油管试验的样本量非常少,试验数据仅有2个,在有限的样本下为评估旧油管和新油管的疲劳寿命,本文采用扩展的Bootsrap方法。
3.1 扩展的Bootsrap方法
Bootstrap方法是美国斯坦福大学统计系教授BradleyEfron于1979年提出的一种新的统计推断方法,是一种只依赖于给定的观测信息,而不需要其他假设和增加新的观测的统计推断方法[6]。Bootstrap方法的目的是用现有的样本去模仿未知的分布,充分利用样本本身的信息,且总体分布不需要做出假设,适用于小子样试验评估,通常以样本量n≥5比较合适[7]。
一般结构疲劳寿命值服从对数正态分布和威布尔分布。针对疲劳寿命服从对数正态分布情况,本文在参考文献的基础上,发展提出将子样数从n=1虚拟扩展成n=7,再进行极小子样结构疲劳寿命的试验评估。
假设原始样本量为n=1,即试验为单子样。假定由类似件试验分布形式为正态分布,且假设标准差σ已知,为使虚拟增广得到的样本更合理,根据其对称分布的密度函数形式,采用以下经验公式虚拟增广原始样本
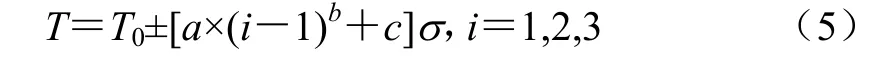
式中:T0为原始样本的均值;σ为类似件的标准差;T为虚拟增广后得到的样本值;a、b为参数,描述虚拟增广点的分散特性的控制系数(依靠工程经验取值,不同的场合参数a、b的取值有所不同,需要与实际试验结果进行比较,权衡决定);c是为了满足立论依据的限制条件及样本服从正态分布特点而待定的常数。
由式(5),假设已知服从正态分布的样本值为T0,于是这 7个点可以取为(T0-1.367 8σ),(T0-0.602 0σ),(T0-0.198 0σ),T0,(T0+0.198 0σ),(T0+0.602 0σ),(T0+1.367 8σ)。
经过反复试算后,取a=0.8,b=1.3较为合适,则根据虚拟增广样本方法的立论依据应该有下面的方程组,联立求解下面方程组可得c值
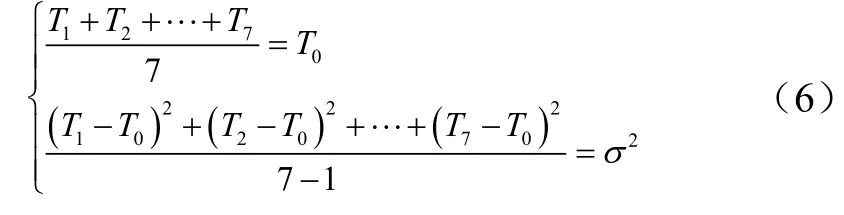
计算结果为c=-0.602。故得虚拟增广样本点从小到大依次为:(T0-1.3678σ),(T0-0.6020σ),(T0-0.1980σ),T0,(T0+0.1980σ),(T0+0.6020σ),(T0+1.3678σ)。
若T0是来自于寿命服从对数正态分布的总体,则Y=lgT服从正态分布,接着和上述方法类似,对服从正态分布的Y进行评估,最后再转化为对服从对数正态分布T的评估。
在考虑置信度时,讨论的是子样均值的分布而不是Y的分布,因此,当n从1虚拟增至7时,由数理统计的知识可知,分布的标准差会乘以为了纠正这个问题,在虚拟增试验点时,应把σRYR改为σRY, eqR(当量σRYR),而σRY,所以n扩至7取YRiR为 :(YR0R- 1.3678σRY.eqR),(YR0R-0.6020σRY.eq)R,(YR0R-0.1980σRY.eqR),YR0R,(YR0R+ 0.1980σRY.eqR),(YR0R+0.6020σRY.eqR),(YR0R+1.3678σRY.eqR)。
非参数 Bootstrap方法无需对总体分布类型做任何假设[5],就可以运用Bootsrap样本对总体F进行统计推断,而且适合于小样本,因而应用广泛。因为该方法计算量非常大,依据统计规律服从 Weibull分布的试验样本可以近似于对数正态分布规律分析,且手工计算几乎不可能完成,本方法利用数直计算软件 MATLAB实现,计算在寿命均值在置信水平0.95的单侧置信区间(下限)。
3.2 寿命评估结果
将旧油管和新油管试验的2个数据取均值,以此为单样本进行虚拟增广原始样本,以虚拟样本为基础采用Bootstrap方法,并通过MATLAB编程进行10万次仿真计算,最终得到在置信度为95%的条件下的旧油管和新油管疲劳寿命下限,见表2。

表2 旧油管和新油管的评估结果
从表2可知,新工艺焊接的新油管试样疲劳寿命优于原工艺焊接的旧油管试样。
4 结论
本研究通过对调距桨外油管加速寿命试验数据折算和极小子样评估,有效预测了旧油管和新油管在95%置信度的疲劳寿命,证明了新工艺油管的疲劳寿命特性优于旧油管,对于提高船舶安全性有重要参考。
此外,由于试验样本量极少,本文提出的方法所评估结果的绝对值可能与真实值存在一定差距,但可用作不同极小样本组评估结果的对比分析,具有较强的工程应用价值。

