一道导数双变量不等式证明题的多角度探究
安徽省合肥市第一中学 (230601) 孔祥士
一、试题呈现
(合肥一中2019-2020学年度高三数学周测二第19题)已知函数f(x)=ex-ax,a∈R.
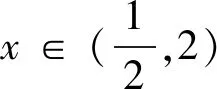
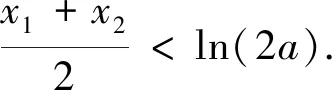
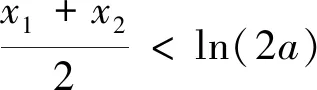
二、多维探究
探究1 由x1,x2为方程g′(x)=0的两根,原不等式可以消去参数a,转化为关于x1,x2的不等式,整体换元令t=x1-x2,转化为关于t的单变量不等式证明.
解法1:由g(x)=ex-ax-ax2,故g′(x)=ex-2ax-a,x∈R.
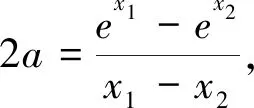
探究2同探究1消去参数a,转化为关于x1,x2的不等式,通过换元,把指数不等式转化为对数均值不等式,进而解决问题.
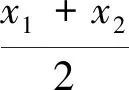
探究3通过求导g′(x)=ex-2ax-a,二次求导,讨论参数a,易得x1 解法3:因为函数g(x)恰有两个极值点x1,x2,所以g′(x)=ex-2ax-a在R上有两个变号零点x1,x2.又g″(x)=ex-2a,当a≤0时g″(x)>0,所以g′(x)在(-∞,+∞)上单调递增,所以g′(x)在R上至多一个零点,不合题意.当a>0时,当x∈ (-∞,ln2a)时g″(x)<0,g′(x)单调递减;当x∈(ln2a,+∞)时g″(x)>0,g′(x)单调递增,又因为当x→+∞时,g′(x)→+∞;当x→-∞时, 探究4 同探究1消去参数a,转化为关于x1,x2的不等式,不妨设x1 导数是高中教学的一个重点,也是一个难点,双变量不等式的证明是导数考察的一个热点,导数与不等式综合解答题对学生数学思维能力要求很高,深刻考察学生的综合能力和核心素养,通常以试卷压轴题出现,很多同学素手无策,它成为很多同学难以逾越的障碍,由于试题综合性强,难度大,更不易搞题海战术,这就更加要求老师在教学中精选例习题,通过对典型问题的多角度探究和适当变式,让学生深刻领悟问题的本质,掌握解决问题的一般方法,体会其中蕴含的数学思想,从而最大限度地提高课堂教学效率. 提升学生的数学素养,落实立德树人的教育教学任务,所有问题都要落实到课堂教学这个主阵地上,尤其是鼓励学生提出问题,用不同的途径解决问题,解题后的深度总结和反思等方面做一些扎实的工作[1].同时也从数学本身的美,激发学生对数学学习的乐趣与热情.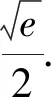
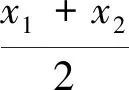
三、教学启示

