巧借错例,正确区分“周长”和“面积”
赵国明
【摘 要】 小学三年级学生正处于由具体形象思维向抽象思维转变的时期,他们能进行一定的抽象思维,但仍以形象思维为主。周长和面积是小学阶段空间与图形领域中的基础内容,本文通过错例分析,正确区分周长和面积。
【关键词】 周长 面积 错例
教学中常见这种现象:图形的“周长”“面积”都学完之后,尤其到高年级,在做题或解决实际问题时,经常有学生混淆图形的“周长与面积”。是学生马虎吗?学生马虎的深层次原因是什么?
一、教材编排分析
从教材编排的内容来看,这些内容的教与学,是在学生已经掌握了长方形和正方形的直观认识、特征,并会计算长方形和正方形的周长的基础上进行的。长方形和正方形的周长与面积学习为其他平面图形的面积与周长扫清障碍,起着承上启下的作用。
二、结合教材及《数学课堂作业本》上的习题进行分析
1. 周长和面积概念不清。
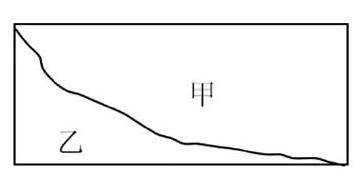
错例1:如图,长方形被分成甲、乙两部分,这两部分比较,( )
A. 周长和面积都相等
B. 周长和面积都不相等
C. 周长相等,面积不相等
课本中对周长的定义是“封闭图形一周的長度就是它的周长”。从这个定义中我们要强调一定要是“封闭图形”,还要理解“一周”这两个关键的地方。“封闭图形”我们很容易,可以找一组图形既有封闭又有不封闭让学生进行比较就很容易得出;而理解“一周”就有一定的难度,曾经听到过一位老师上过《周长》一课,她对“一周”是这样解释的:她以小蚂蚁爬树叶来解释一周的概念。A是在图形的里面跑来一圈。B是沿着树叶的边沿走,但是没有封闭。C是沿着树叶的边沿走了一圈。通过这样的对比练习学生很清楚的知道“一周”的概念。从周长的定义中我们可以看出,周长的单位应该是一个长度单位。课本对面积的定义是“物体的表面或封闭图形的大小,就是它的面积”。一个专家曾对面积做了三个要素:一是面积应该是封闭的,有边界线,不开口,内部的大小是面积;二是图形面积的大小与周长有关,与边界线的长短有关;三是面积是各部分之间和(密铺),是可测量的,可加、减。小学生概念的建立离不开辨析,对于三年级的学生来说,正反例的对比更加有效。在上面积的概念的时候,我顺势就让学生说一说什么是周长,同时让学生自己去摸一摸桌面的“周长”和“面积”。学生通过对比摸知道了这两概念的不同之处,一个是边沿一周的长度,另一个是内部的大小。
2. 对长方形、正方形周长、面积公式的不理解,导致题意的理解错误。
错例2:在方格纸上画几个长方形或正方形,使它们的周长都是12厘米,然后比较一下它们的面积。你能发现什么?
有部分学生是画出了下面的几种情况:A长:12厘米,宽:1厘米 B.长:6厘米,宽:2厘米 C.长:4厘米,宽:3厘米。要画一个长方形、正方形,必须知道长方形的长和宽或者是正方形的边长,牢牢地抓住这一点。再从周长的定义出发,是一周的长度,对于长方形来说就是2条长加上2条宽,所以画长方形的时候我们可以是12÷2=6(厘米),求出一条长加一条宽的和。接下来的话可以任意的规定长是5厘米,宽是1厘米;长是4厘米,宽是2厘米;边长是3厘米。
3. 学生缺乏转化、整体减局部的思想。
错例3:教室前面的墙壁,长6米、宽3米。墙上有一块黑板,面积是3平方米。现在要粉刷这面墙壁,要粉刷的面积是多少平方米?
班级中有一部分的学生的答案是这样的:6×3=18(平方米)18÷3=6(米)。学生怎么会出现如此的答案?我让孩子们抬起头观察我们教室前面的墙壁,我说:“如果是让你粉刷这堵墙,你会吗?”有学生回答:“会啊。”“那怎么刷?”“直接刷黑板除掉的地方。”“那对了,我们这道题目也是刷黑板除掉的地方啊。”学生“哦”一声。终于明白了只要6×3=18(平方米)18-3=15(平方米)。其实我们可以先求出总的面积,再在总面积中除掉一部分就是剩下的面积了。
错例4:一张边长是10厘米的正方形纸中,剪去一个长6厘米、宽4厘米的长方形。小明想到了三种方法。剩下部分的面积是多少?剩下部分的周长呢?
根据题意,大的正方形剪去一个长方形,那面积的大小就是正方形的面积剪去长方形的面积,用整体剪去部分就是剩下的面积。而剩下部分的周长我们就要采用转化的思想,第一幅我们可以把6厘米和4厘米分别往外面移,刚好跟原来的长方形周长相等;第二幅用同样的方法把6厘米往外面移,剩下的周长就是原来长方形周长再加2条4厘米的边;第三幅是把4厘米往外面移,剩下的周长是原来长方形周长再加2条6厘米的边。从这道题中我们明显的感觉出转化、整体减局部的思想给我们的解题带来很大的方便。在平常的教学中我们要慢慢地渗透这种思想,让学生能从另一个角度来思考问题,开拓他们解题的思路。
“周长”与“面积”是小学数学“空间与图形”领域的重要内容,小学生从学习周长到学习面积,从长度单位过渡到面积单位,是空间形式认识发展上的一次飞跃。搞清楚两者之间的关系,为学生后续关于“空间与图形”的学习,扫清很多障碍,值得我们一线老师重视。

