等效电源法的应用

王彦芸

摘要：文章阐述了等效电源的理论依据，结合实例介绍了等效电源法在一些电路问题中的应用，通过分析例题深刻感受等效电源法的妙用。

关键词：戴维南定理;等效电源法;误差分析

中图分类号：G642.0     文献标志码：A     文章编号：1674-9324（2020）15-0284-02

高中物理恒定电流部分，經常分析一些复杂电路中电流、电压变化问题，解决的方法是根据闭合电路欧姆定律采用分析法逐步得解，这种方法十分烦琐。针对这一问题我们介绍一种简单的方法——等效电源法.它把较复杂的含源部分电路等效为一个新的电源，可使问题简化，从而避免不必要的分析和复杂的运算，优化解题思路，提高解题效率。

一、等效电源的理论依据

等效电源法的理论依据是戴维南定理，其内容为：任一线性有源二端网络可用一恒压源与一个电阻的串联来等效替换，恒压源的电动势等于被换网络的开路电压，串联电阻的阻值等于被换网络的除源网络的等效电阻。电源的电动势和内电阻是电路的主要参数。一段含源电路等效为新电源后，其新电动势和新内电阻怎样确定呢？有戴维宁定理可知：新电动势等于新电源两端开路时两极间的电压，新内阻等于从两端看除源电路（电源仅看作电阻）的等效电阻，根据电路的串并联结构把含源电路分为两类并分别计算其电动势E′和内电阻r′。

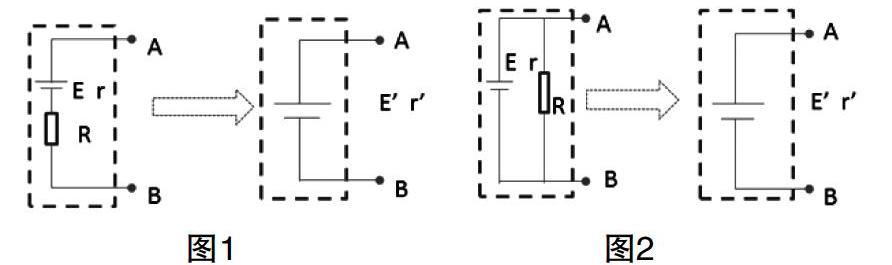
1.实际电源（电动势E，内阻r）与电阻R串联在一起形成部分电路，构成一个等效电源如图1，把虚线框内电路看作新电源，则电动势E和内阻r分别为：E=E，r=r+R。

2.实际电源（电动势E，内阻r）与电阻R并联在一起形成部分电路，构成一个等效电源如图2，把虚线框内电路看作新电源。则电动势E和内阻r分别为：E=ER/（R+r） r=Rr/（r+R）。

二、等效电源的应用

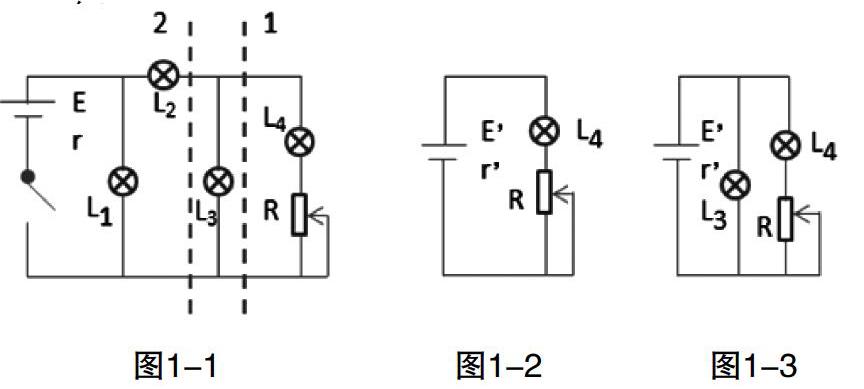
1.动态电路中相关问题的分析。当外电路中接入可变电阻时，此电阻的变化会导致电路中的路端电压、总电流、总电阻的变化，此时可把不变的部分与电源等效为新电源，然后再分析问题，可使问题得到简化。

2.分析测电池电动势和内电阻实验的系统误差。测电池电动势和内电阻实验的实验中，由于电压表和电流表都有内阻，造成实验出现了系统误差，使测量值和真实值出现了偏差，利用等效电源法来分析方便快捷。该实验的理论依据是闭合电路的欧姆定律，表达式为E=U+Ir，U为路端电压，I为干路电流，该实验可采用电流表外接法（图2-1）和电流表内接法（图2-2）。电压表 的作用是测量外电压U，电流表？髿的作用是测干路电流I。

参考文献：

[1]梁灿彬，等.电磁学[M].北京：高等教育出版社，1980.

[2]刘管福.邱晓蓉.等效电源法[J].物理教师，2005，（3）.

[3]张知礼.巧妙利用等效电源法解电路问题[J].湖南中学物理，2013，（12）.

[4]王松涛.等效电源法测电源电动势和内阻实验系统误差分析[J].物理通报，2014，（11）.