混凝土柱二阶效应计算的μ诺模图

章胜平， 陈 旭， 赖应良a， 毛德均， 吴克川

(1. 昆明理工大学 a. 建筑工程学院； b. 管理与经济学院， 云南 昆明 650504；2. 昆明学院 建筑工程学院， 云南 昆明 650214)

当今先进的计算机软件为设计师们提供了极大的工作便利，但另一方面也削弱了他们对设计方法的理解和计算结果的判断能力。在计算理论发达的德国、日本等国家，在应用软件的同时还非常注重设计师的手算复核能力的培养。

混凝土结构仍是应用最广泛的结构，随着高度增加和高强度材料的应用，基于变形后结构的二阶分析与设计更为重要[1]。二阶效应会增大结构或构件的变形和内力，相当于降低了结构或构件的刚度和承载力，如果在设计中忽略二阶效应，相当于降低了结构设计的安全度[2]。至今对简化二阶效应计算方法已开展了大量有益研究[3]，我国混凝土设计规范[4]在结构分析上区分有、无侧移，在截面配筋设计上区分轴压、小偏压和大偏压给出了不同的计算公式，使用不简捷。本文对二阶效应计算的μ诺模图法[5]进行了推导，对其背后的理论进行了分析和解释，期望对我国混凝土结构实用计算方法理论发展起到积极作用。

1 模型柱分析

任何结构中的柱都可简化成模型柱，简化的假设是：模型柱上的二阶位移与该柱在原结构中的二阶位移相等。通过确定该柱在原结构中计算长度l0，将l0代入模型柱中，这样就建立起了模型柱与原结构中该柱的联系。换言之，模型柱法是将构件从整体结构中剥离出来，以l0来考虑结构与构件之间的各种联系，如端部约束、侧向约束(有侧移还是无侧移)。按照弹性稳定理论，由结构屈曲图形获知计算长度l0。如图1(图中：N为轴力；Δ为侧移；δ为挠曲变形；l为柱的实际长度)，视横梁刚度的不同，在无侧移时框架柱的l0为实际长度l的0.7～1倍，在有侧移时为2～∞倍。ACI 318《美国混凝土结构规范》给出了l0的计算诺模图，JTG 3362-2018《公路钢筋混凝土及预应力混凝土桥涵设计规范》[6]给出了l0的解析式。有侧移结构柱的l0比实际长度大很多，长细比大，由于二阶效应与长细比的平方成比例，故有侧移结构的二阶效应显著，如活动支座高墩。有侧移结构只需考虑P-Δ效应(侧移二阶效应)，因为有侧移结构的P-δ效应(挠曲二阶效应)与P-Δ效应相比相对很小(见图1b)，常忽略不计。因此，GB 50010-2010《混凝土结构设计规范》[4]区分P-δ效应和P-Δ效应给出了不同计算方法，在有侧移的P-Δ效应计算上要区分荷载能否引起侧移，在截面配筋设计上要区分是轴心受压、小偏心受压还是大偏心受压而用不同的公式。

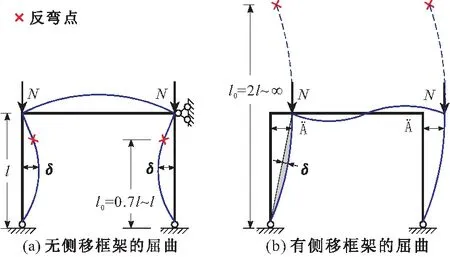
图1 计算长度

剥离出来的悬臂模型柱，可以考虑水平等各种荷载，不用区分P-Δ效应和P-δ效应，不用区分是否有侧移。将混凝土构件出现的混凝土开裂、钢筋屈服等材料非线性，反映在曲率图里面，再将弯矩图与曲率图相图乘，则悬臂模型柱就考虑了混凝土结构中的双重非线性(几何非线性和材料非线性)，见图2(图中：H为水平力；M为弯矩；M1N为轴力产生的一阶弯矩；M1H为水平力产生的一阶弯矩；e1为一阶偏心距；e2为二阶偏心距)。基于模型柱，配套相应的μ诺模图，便可以方便地实现二阶效应的实用计算。

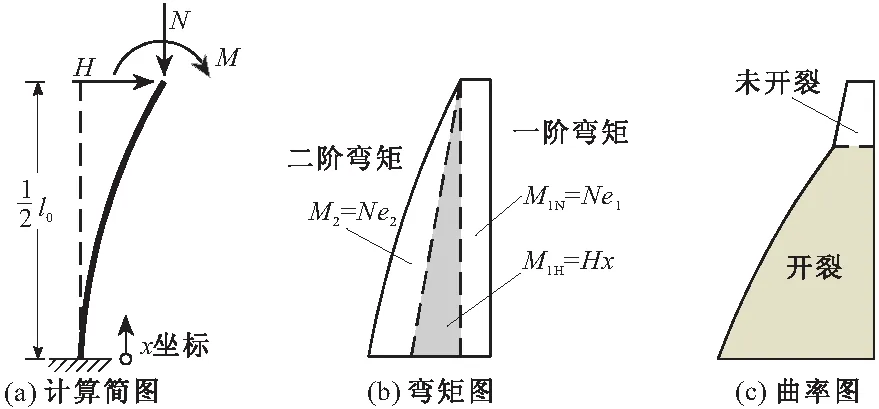
图2 悬臂模型柱

对混凝土结构按照小变形理论可知，曲率等于挠度的二阶导数，变形协调方程为二阶微分方程，所以考虑几何非线性是一个二阶问题。因此在模型柱中，按照二阶理论，计算二阶偏心(附加变形)，再计算二阶弯矩(附加弯矩)。

在模型柱中，材料非线性通过非线性的弯矩-轴力-曲率相关关系[7]来考虑，而不从材料的刚度变化来考虑。因为给定混凝土截面尺寸，还不能确定最终的截面，混凝土很容易开裂，一旦开裂，就有部分混凝土退出工作，钢筋的面积还是待求的未知量。通过计算曲率φ可以避开这些问题，也就是说可以不用知晓开裂的情况和钢筋面积，只要知道截面两边的应变(受压边缘应变εc和受拉钢筋应变εs)，就可确定曲率。而εc和εs又可分别取很多不同的值和组合，要精确计算又要借助数值方法。为此简化处理，直接取它们的极限值，即受拉和受压钢筋的屈服应变，进而得到相应的屈服曲率。换言之，模型柱法是直接由曲率计算二阶效应的一种直接设计法，避免了估计非线性刚度[8,9]的难题。

2 二阶静力平衡方程

2.1 二阶偏心距计算

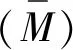
研究表明，不同曲率分布对二阶偏心距的结果影响并不大(见图3)。当细长柱的曲率为抛物线分布，抛物线曲率分布的二阶偏心距e2为：

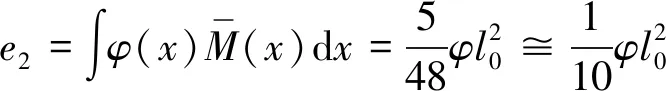
(1)

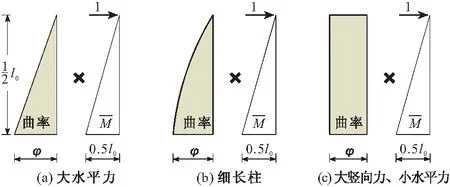
图3 曲率分布的影响

由此可见，通常抛物线曲率分布的结果介于两种极端荷载情况的中间，即便出现极端情况偏差也仅约为20%。所以最终的曲率分布假设为抛物线分布。

2.2 弯矩计算

假设图2a所示的力和弯矩为正方向，则柱底截面弯矩为：

M=M1H+M1N+M2=0.5Hl0+N(e0+ea+e2)

(2)

式中：初始偏心e0=M/N；ea为考虑构件几何缺陷的附加偏心距。

将式(1)代入式(2)得：

(3)

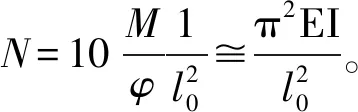
这时的轴力相当于欧拉屈曲荷载，即EI为常量，也就是说欧拉屈曲荷载是以整个杆件的EI为常量出发的。而对于钢筋混凝土构件，尤其是混凝土开裂和钢筋屈服后，实际情况EI沿杆长是变化的，EI为常量仅是一特例。

2.3 曲率计算

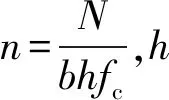
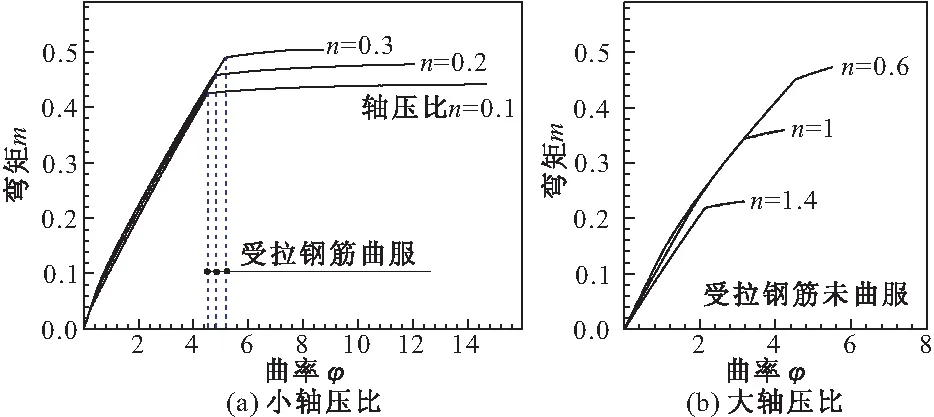
图4 曲率分布的影响

研究表明，在大轴压比的小偏心受压区，曲率与轴压比和强度配筋率的关系如图5[11]所示。

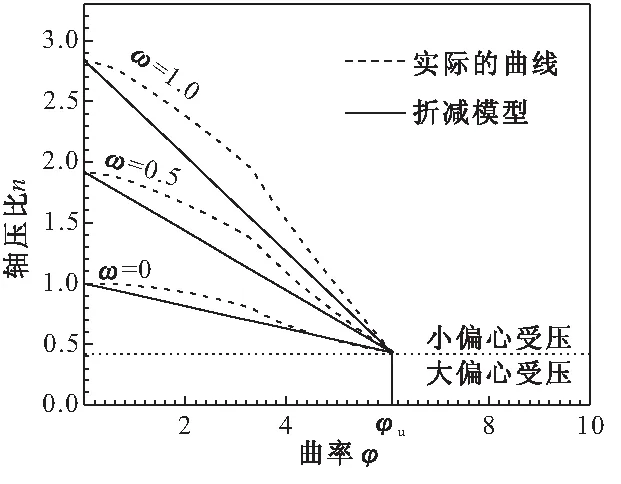
图5 轴力-曲率关系

因此，曲率φ的计算模型为：

(4)

式中：Ncu为截面轴心受压极限轴力，由截面承载力确定；极限曲率φu的计算式为：

φu=2εy/(h-2as)

(5)

式中：εy为钢筋屈服强度设计值；as为受拉钢筋合力至截面近边缘的距离。

2.4 静力平衡方程

细长柱的破坏属于材料强度破坏，构件极限承载力等于截面极限承载力Mu，则有：

(6)

将式(6)改写为无量纲形式：

(7)

式中：长细比λ=l0/h。

此至，式(7)给出了基于模型柱的混凝土压弯构件二阶计算的一种简化方法。该方程左边的截面承载力mu与截面材料、形状和配筋有关，右边与柱的受力、长细比和截面有关，虽然借助于计算机不难得到解析解，但运用诺模图技术可获得一种更为直观和直接的解答方式。

3 μ诺模图

诺模图是将方程组所有的可能解用图形方式表达，通过查图的方式实现非线性方程组的求解，在工程中有大量的应用。二阶效应计算的μ诺模图与计算公式法比较，虽然从表面上看，查图表在操作上复杂一点，但从前面的推导过程可见，诺模图法计算原理清晰、方法精细。诺模图法也补充了一种快速设计和估算的手算方式，能够方便地用于手算和有限元结果的验证。

3.1 图形的绘制

采用平行坐标系，分别以无量纲弯矩和长细比为左右坐标，见图6。

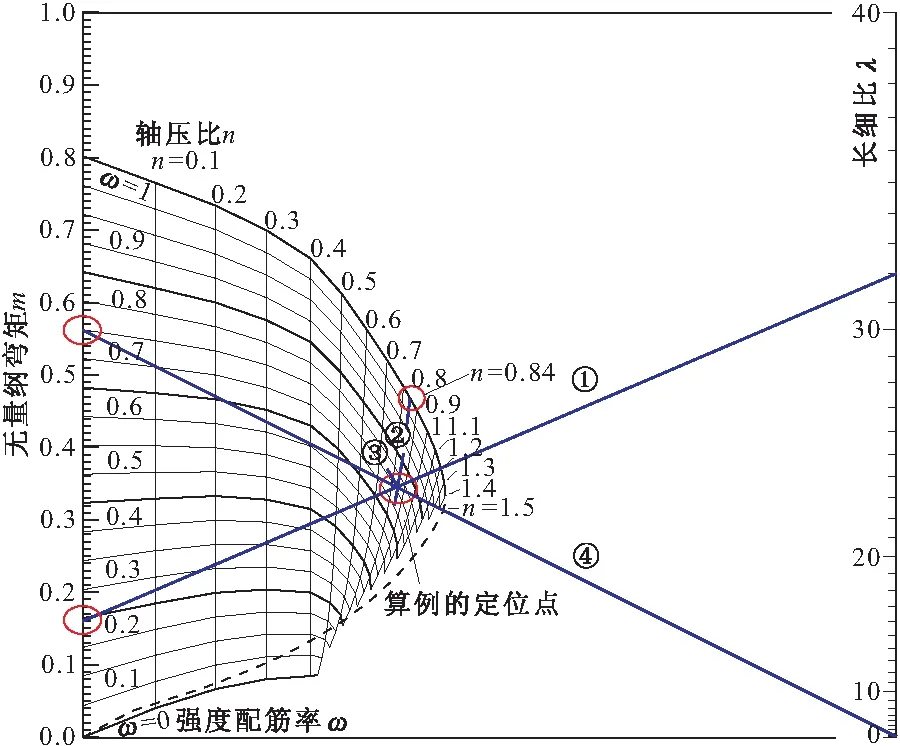
图6 μ诺模图

假设截面为矩形、对称配筋，受拉钢筋合力至截面近边缘的距离as=0.1h，钢筋屈服强度设计值fy=435 N/mm2，拉压强度相等。选择强度配筋率ω由0到1之间等间隔变化的21个值，得到21条ω不变的横向设计曲线；选择轴压比n由0～1.5之间等间隔变化的15个值，得到15条n不变的纵向设计曲线，这就是μ诺模图(图6)。μ诺模图将轴压比、一阶弯矩、弯矩设计值、配筋和长细比五个变量，表示在一张图里面，构思精巧。另外，采用无量纲图表，图表数量大为减少，使用更为方便。

从图6可以看到，当轴压比小于0.4时，在ω=0～1.0 范围内都有解。而随着轴压比的增加，可求解的区域(能得到强度配筋率的范围)在逐渐减小。

3.2 算 例

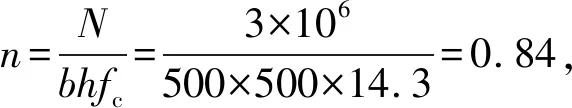
连接m1=0.16与λ=32得到第①条线，由内插法找到n=0.84的第②条线，由①和②的交点，得到第③条线，ω=0.72，钢筋面积As为：

连接①和②交点与长细比0点得第④条线，总弯矩mtot=0.56，柱底弯矩设计值Md=mtotbh2fc=0.56×5003×14.3×10-6=1001 kN·m。

在算例中，由轴压比、一阶无量纲弯矩和长细比三个已知量，作出图6所示的辅助线①②③④，在图中定位一个点，便可直接得截面配筋和弯矩设计值。反之，按照④③②①的顺序，则可进行截面配筋校核。

4 结 论

基于悬臂模型柱，给出了混凝土柱二阶效应计算的μ诺模图。该图同时考虑的二阶几何非线性和材料非线性，可以方便地实现二阶效应的实用计算，为快速设计和估算提供了一种方法，为有限元计算提供了一种验证手段。与我国混凝土结构设计规范中的方法比较，不用区分是否有侧移或无侧移，不用在有侧移时对荷载区分是否引起侧移，仅用一张图便可直接查询涵盖轴压、小偏压和大偏压的钢筋面积。

模型柱法与对模量E折减考虑材料非线性的刚度法有本质的不同，它是直接由承载力极限状态的极限曲率来计算二阶效应的一种直接设计方法。μ诺模图构思精巧，一张图表示了轴压比、一阶无量纲弯矩、弯矩设计值、配筋和长细比五个变量之间的逻辑关系，能够直接用于短柱和细长柱的配筋设计和配筋校核。