转体桥混凝土球铰磨心接触应力参数分析

范剑锋， 刘 涛， 彭自强， 尹耀霄， 王 佶

(武汉理工大学 土木工程与建筑学院， 湖北 武汉 430070)

桥梁转体施工[1,2]适合跨越既有铁路线、深谷等施工条件受限的场地。转体桥球铰[3]是此类结构最关键的结构构件。转体球铰分为钢球铰和混凝土球铰，钢球铰以其制作精度高，运输吊装工艺成熟而多用于城市及交通便利地区。混凝土球铰因为不需要大型运输吊装器械，在山区大跨桥梁建设中广泛运用[4]。混凝土球铰的设计要考虑到与模架施工、转动体系布置、转体施工准备及转体稳定性控制，是桥梁转体施工中的关键技术[5]。球铰的正常工作需保证表面接触应力处于准确受控状态，但对球铰磨心设计参数的研究较少。在以往的转体桥球铰设计中，都是先将球铰的球面假定为平面，进行平面的尺寸设计[6]，这样带来最大的误差就是球铰表面接触应力计算不精确。车晓军等[7]通过球铰表面应力差来预估转体桥的不平衡力矩。左敏等[8]基于弹性半空间理论推导了球铰接触应力的计算公式，验证了球铰强度理论相比于规范简化算法的优越性。范剑锋等[9]提出基于非赫兹接触理论的磨心表面接触应力公式。傅贤超等[10]通过对比平面铰和球铰，论证了平面铰受力性能更加合理。

综上研究成果，球铰的设计、监控中有如下不足之处：(1)球铰简化为平面进行参数设计带来误差；(2)弹性半空间理论适用于非协调接触[11]，球铰接触应力采用弹性半空间理论进行计算，虽结果相近，却不具有代表性；(3)球铰设计参数研究较少。

由于在球铰参数设计角度上，缺少参考性研究成果，因此本文运用基于非赫兹接触的理论解法与有限元模拟软件，对球铰矢高变化、球铰半径变化及同一矢径比不同球铰半径变化进行了理论计算和有限元模拟，以球铰表面接触应力为目标，对比分析了不同设计参数下，球铰磨心接触应力的分布，并分析球铰磨心参数的敏感性。

1 非赫兹接触理论应力计算

范剑锋等[9]在基于非赫兹接触理论的基础上，提出了磨心表面接触应力的公式，合力F和应力分布p(x)为：

(1)

(3)

(4)

式中：F为总荷载；r为接触带宽；E*为当量弹性模量；A2为非赫兹接触应力Steuermann模型中的系数；E1，E2分别为两弹性体的弹性模量；μ1，μ2分别为两弹性体的泊松比；R1，R2分别为两接触面的上、下半径。

若上下两接触面R1=R2，取R1=R2(1.0207-0.0024lnR2)。

接触带宽r为：

(5)

式(1)为轴对称共形接触(即协调接触)结构荷载函数，式(2)为轴对称共形接触应力分布值。

2 混凝土球铰磨心参数分析

本文以南渡江转体拱桥为依托，转体桥球铰磨心作为研究对象，以球铰磨心上表面应力为参数目标，对球铰尺寸参数进行敏感性分析。通过有限元模拟方式进行参数敏感性分析，并将结果与理论解进行对比分析，拟合出球铰参数敏感性参考公式。其中，实际球铰磨心尺寸如图1，其材料力学参数如表1。

图1 球铰磨心尺寸/mm

表1 材料力学参数

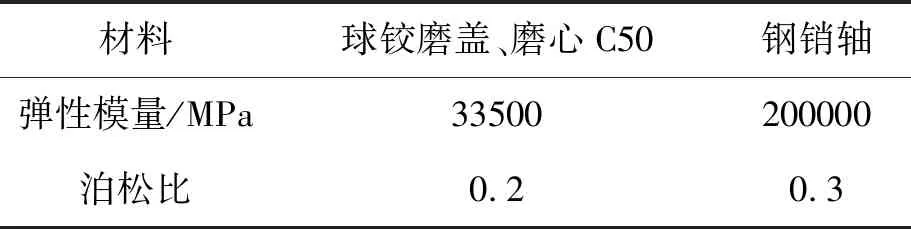
材料球铰磨盖、磨心C50钢销轴弹性模量/MPa33500200000泊松比0.20.3

运用通用有限元软件ABAQUS建立球铰磨心模型，由于ABAQUS无固定量纲，模型长度单位取mm，力取N，则相应的应力单位为MPa。采用径向六面体分割单元。全桥重量为56900 kN，施加在球铰磨盖上表面。施加作用力时，分为两步，第一步施加10 kN的力，以防止直接施加全桥重量导致计算不收敛；第二步施加全桥重量。球铰下磨盘底部边界全部约束。选择CPRESS查看球铰磨心上表面应力。上磨盖、下磨心与定位销轴模型如图2所示。

图2 有限元模型

球铰的力学模型示意图如图3所示(图中：1为上转盘；2为下转盘；3为撑脚；4为上球铰；5为

下球铰；R为球铰半径；R、为球铰平面半径；α为球铰支撑圆心角或球铰外边缘圆心角；θ为球铰径向角度)。

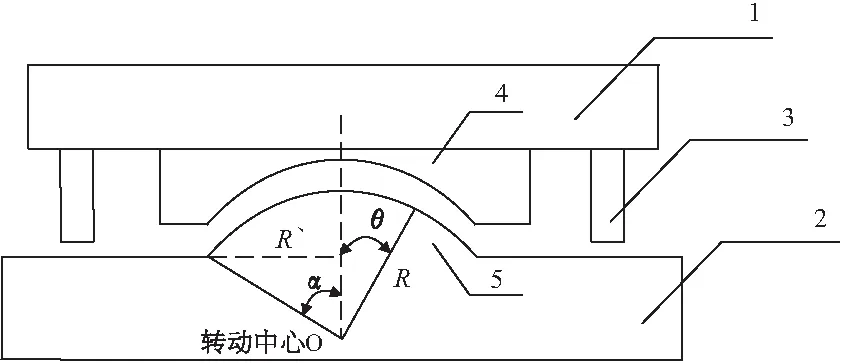
图3 球铰尺寸参数示意

2.1 球铰矢高变化对球铰受力的影响

在同样的荷载作用下，进行球铰矢高参数分析，保持球铰平面半径不变，因此球铰半径会随之变化，在ABAQUS中设置Path路径，从球铰一端至另一端，用来查看球铰磨心表面接触应力，查看组如图4，5所示。

图4 Path路径设置

图5 查看节点示意

球铰接触应力统计见图6。由图6可知，球铰表面接触应力变化趋势不因球铰矢高的变化而变化，球铰表面接触应力都从磨心圆点开始，沿着径向先增加，后减小。同时从图6可以看出，球铰矢高越小时，即球铰越平缓时，表面接触应力分布更加均匀，因为此时更加接近平面。

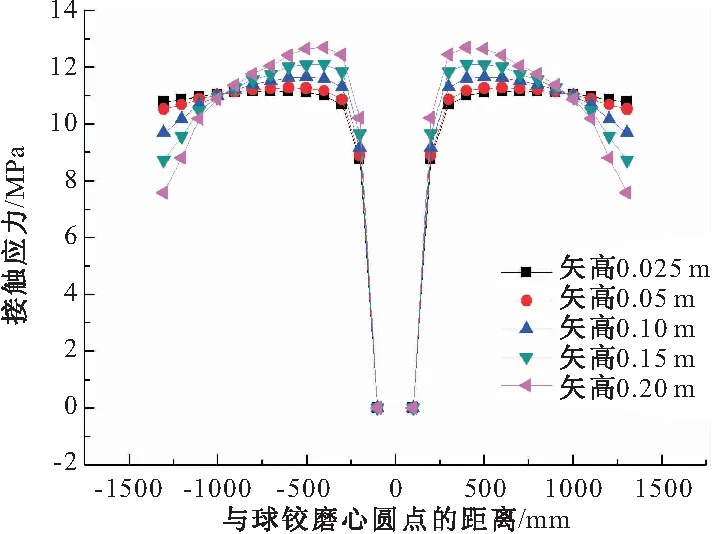
图6 同一球铰半径不同矢高自重荷载下球铰接触应力值统计

将应力最大值进行统计，并将计算参数代入公式(2)中，运用Mathematica计算软件得到应力理论解，并取出最大值。结果统计于表2中。

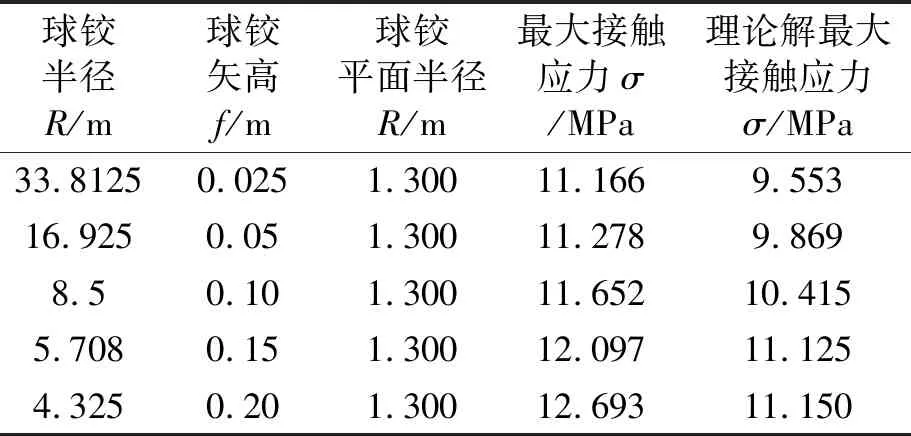
表2 球铰参数与最大接触应力

将不同矢高下的球铰表面最大接触应力统计于图7中。

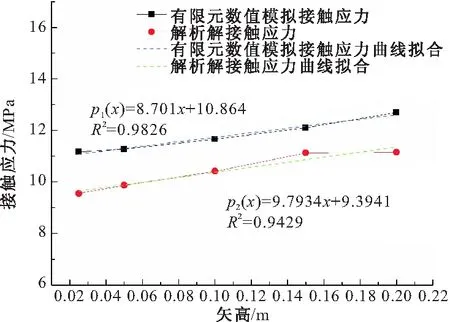
图7 不同矢高最大接触应力结果统计

在自重荷载作用下，当球铰平面半径不变时，球铰矢高变化导致球铰半径变化。由图7可知，此时将有限元数值模拟结果与理论解结果进行统计，并拟合出最大接触应力对矢高变化的公式。图中可明显看出，两者计算结果都呈现出随着矢高增加而最大接触应力增加的上升趋势。

有限元数值计算结果呈明显线性趋势，其最大接触应力拟合曲线为：

p1(x)=8.701x+10.864

(6)

理论解计算结果也呈明显线性趋势，其最大接触应力拟合曲线为：

p2(x)=9.7934x+9.3941

(7)

2.2 球铰半径变化对球铰受力的影响

在同样的荷载作用下，进行球铰半径参数分析，其矢高保持不变。球铰磨心表面接触应力变化规律不变，结果如图8所示。

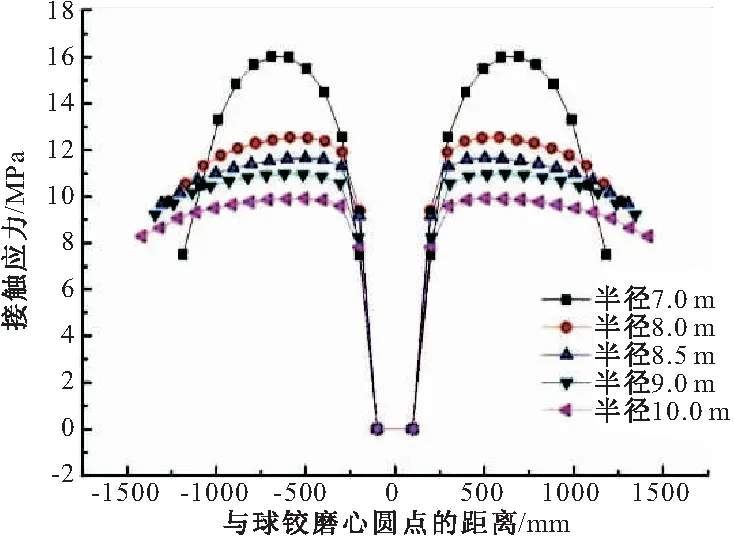
图8 同一矢高不同球铰半径自重荷载下球铰接触应力值统计

由图8可知，球铰表面接触应力变化趋势符合非赫兹接触理论，不因球铰半径的变化而变化，球铰表面接触应力都从磨心圆点开始，沿着径向先增加，后减小。球铰半径越小，其最大接触应力值越大。将接触应力最大值进行统计，可以得到表3。

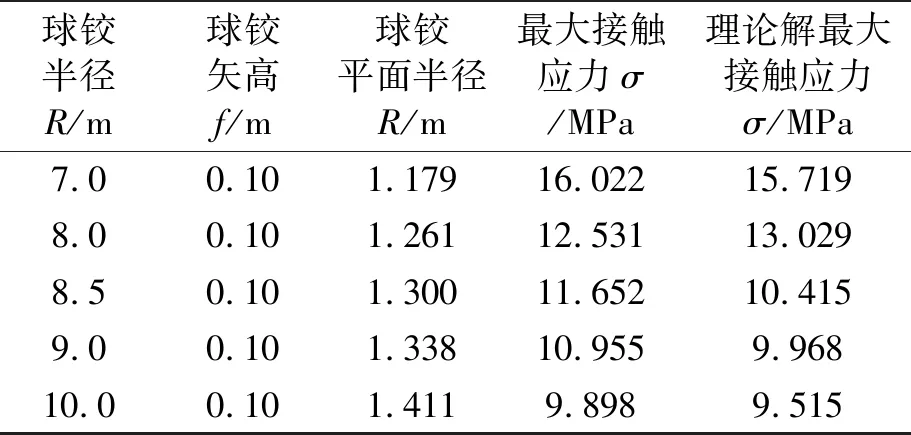
表3 球铰参数与最大接触应力

在自重荷载作用下，当球铰矢高不变时，球铰半径变化导致球铰平面半径变化。由图9可知，此时将有限元数值模拟结果与理论解结果进行统计，并拟合出最大接触应力对球铰半径变化的公式。图中可明显看出，两者计算结果都呈现出随球铰半径增加而最大接触应力减小的趋势。

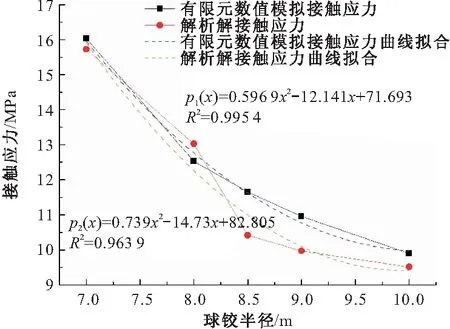
图9 不同球铰半径最大接触应力结果统计

有限元数值计算结果呈弱非线性趋势，其最大接触应力拟合曲线为：

p1(x)=0.5969x2-12.141x+71.69

(8)

理论解计算结果也呈弱非线性趋势，其最大接触应力拟合曲线为：

p2(x)=0.739x2-14.73x+82.805

(9)

对式(8)(9)求导得：

(10)

(11)

2.3 球铰矢高及球铰半径同步变化(矢径比不变)对球铰受力的影响

在同样矢径比及相同荷载作用下，进行球铰半径参数分析，结果如图10所示。

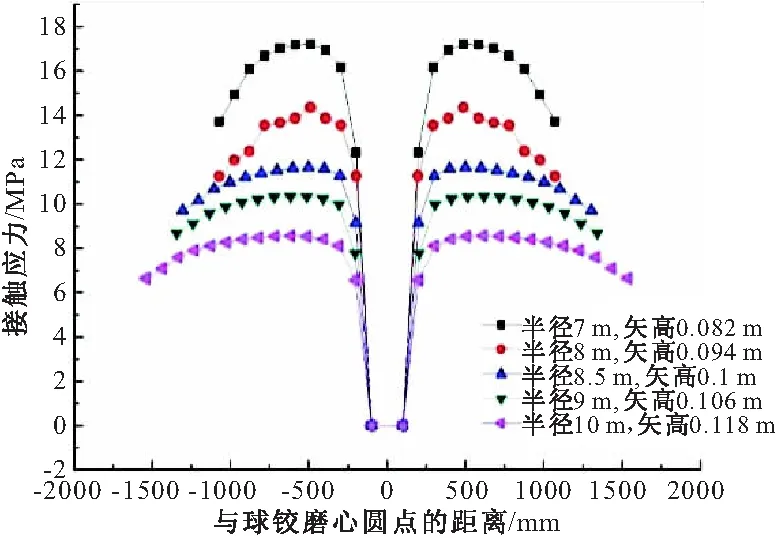
图10 同一矢径比自重荷载下球铰接触应力值统计

由图10可知，球铰表面接触应力变化趋势符合非赫兹接触理论，不因球铰半径的变化而变化，球铰表面接触应力都是从磨心圆点开始，沿着径向先增加，后减小。由于保持同一矢径比，球铰半径小会导致球铰平面半径小，因而最大接触应力会高于球铰半径大的研究对象。

将应力最大值进行统计，可以得到表4。

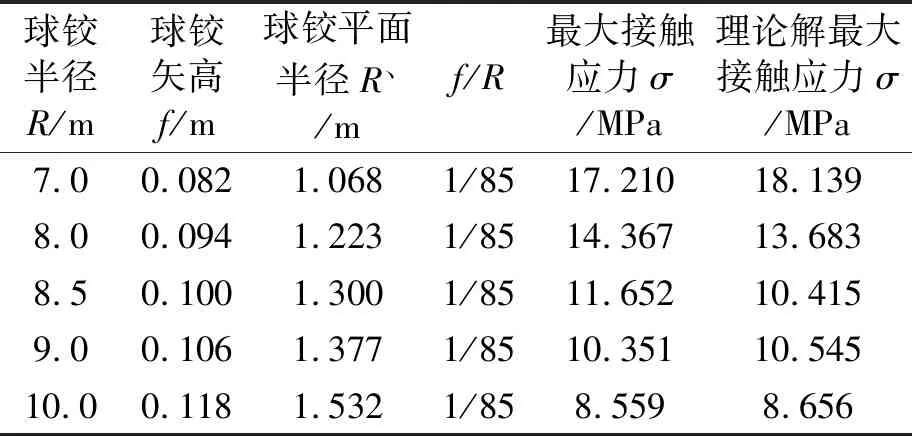
表4 球铰参数与最大接触应力

由图11可知，在自重荷载作用下，当球铰矢径比相同时，球铰半径变化与最大接触应力的变化呈现较明显的线性关系。图中可明显看出，矢径比相同时，半径越大，最大接触应力越大，增大半径对降低接触应力的作用明显。并且有限元数值模拟最大接触应力均大于理论解最大接触应力。

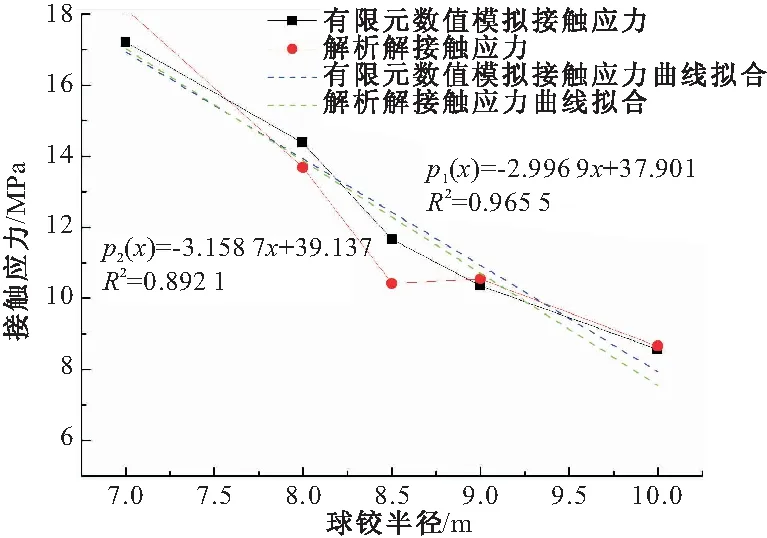
图11 相同矢径比最大接触应力结果统计

有限元数值计算结果呈明显线性趋势，其最大接触应力拟合曲线为：

p1(x)=-2.9969x+37.901

(12)

理论解计算结果也呈明显线性趋势，其最大接触应力拟合曲线为：

p2(x)=-3.1587x+39.137

(13)

根据图7，9，11，计算拟合的式(6)～(13)，结果统计如表5，6所示。

表5 线性拟合统计结果

表6 非线性拟合统计结果

4 结 论

(1)从有限元计算结果可以看出，球铰接触应力表面分布符合非赫兹接触理论，应力分布曲线规律呈现M形，即球铰圆心及边缘处应力相较于球铰水平半径中间部位低。

(2)球铰水平半径不变时，最大接触应力与矢高变化呈明显线性关系；球铰矢径比不变时，最大接触应力与球铰半径变化呈明显的线性关系；矢高不变时，最大接触应力与球铰半径变化呈弱非线性关系。其中球铰矢高变化系数最大，其影响敏感性最大。

(3)在分析球铰半径变化时，有限元数值模拟最大接触应力值与理论解最大接触应力值接近，误差最大值为12%。