大尺寸深埋锚栓套筒装置的抗拉承载力
张晋元, 秦泽斌, 朱 宇, 王金泽
(天津大学 建筑工程学院, 天津 300350)
为更好地进行建筑结构的抗震研究,目前越来越多的高校以及科研单位开始陆续建立地震模拟振动台系统。带端板的锚栓常被用来保证作动器与混凝土基础的可靠连接。目前对于锚栓在混凝土中锚固的研究已有不少成果。在拉力荷载作用下,锚固的破坏形式主要有三种:锚栓的拔断破坏、锚栓的拔出破坏、混凝土的锥体破坏[1]。假设锚栓强度与混凝土承压范围足够大,则锚固的破坏形式为混凝土的锥体破坏[2]。目前对于混凝土发生锥体破坏的计算方法主要有两种:基于45°锥体模型方法(45CM)和混凝土承载力设计方法(CCD法)。45CM最先被提出并被美国混凝土规范ACI 349-85[3]所采用,广泛用于核电设施中。CCD法被美国混凝土规范ACI 318-05[4]及欧洲规范[5]所采用。但是目前的计算方法都是基于浅埋深和较小端板尺寸下的试验结果,而在实际工程中,特别是振动台中,锚栓常常带有较大尺寸的端板且深埋于混凝土中,并且锚固装置并不由单一的锚栓构成,因此不能简单参照现有规范进行设计。本文提出一种用于振动台作动器的锚固装置,装置由带端板的锚栓与套筒组成,整体深埋于混凝土基础中,套筒起到安装定位与保护锚栓的作用,锚栓上部固定作动器端部,具体如图1所示,并在此基础上使用有限元软件ABAQUS进行数值模拟与分析,基于现有规范提出锚固装置受拉的初步设计公式。
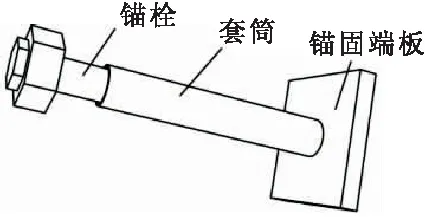
图1 锚固装置示意
1 有限元数值模型
1.1 混凝土属性
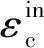
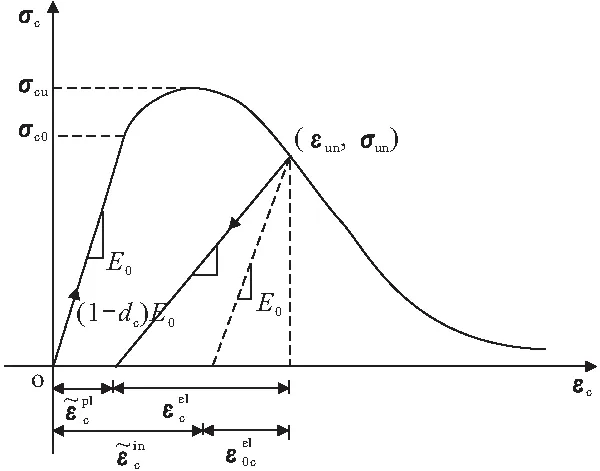
图2 混凝土损伤塑形模型受压应力-应变关系
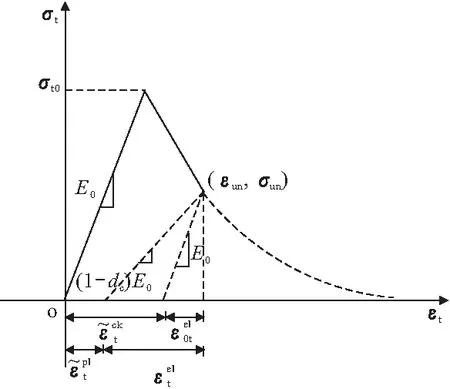
图3 混凝土损伤塑形模型受拉应力-应变关系
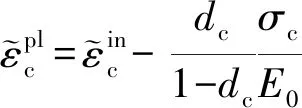
(1)
(2)
E=(1-dk)E0,k=t,c
(3)
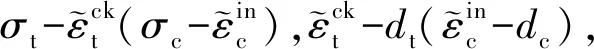
1.2 钢材属性
为保证锚固装置发生混凝土的锥体破坏,钢材假定为线弹性材料,弹性模量为2.06×105MPa,泊松比为0.3。
1.3 单元模拟
本文计算模型如图4所示,锚固端板厚度t均为50 mm,锚栓直径d′比套筒直径d小10 mm,其余几何尺寸见表1。锚栓中心到混凝土块体边缘的距离为埋深hef的2.5倍,从而保证锥体破坏面的形成。
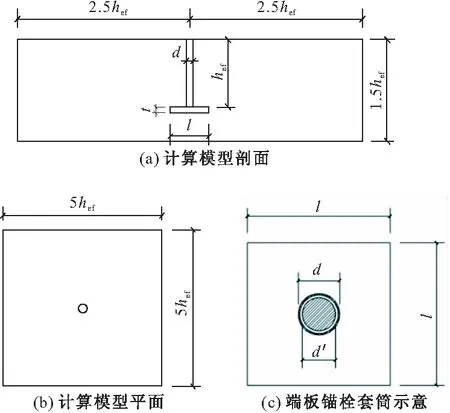
图4 计算模型构造示意
表1 计算模型几何尺寸
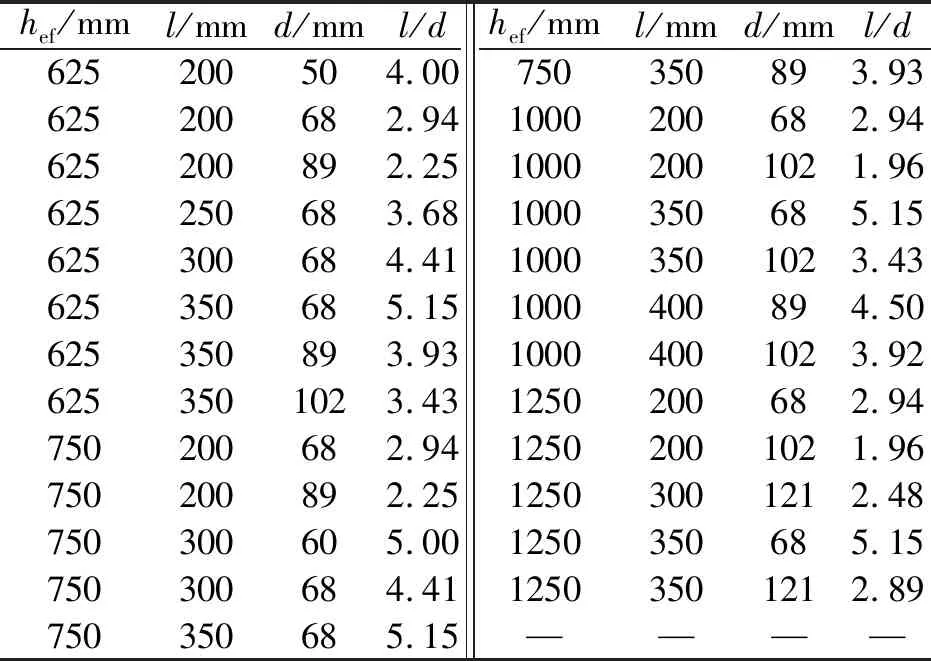
hef/mml/mmd/mml/dhef/mml/mmd/mml/d625200504.00750350893.93625200682.941000200682.94625200892.2510002001021.96625250683.681000350685.15625300684.4110003501023.43625350685.151000400894.50625350893.9310004001023.926253501023.431250200682.94750200682.9412502001021.96750200892.2512503001212.48750300605.001250350685.15750300684.4112503501212.89750350685.15————
由于模型的几何对称性与受力对称性,采用1/4建模方式分别建立各部分的有限元模型。模型均采用8节点的三维缩减积分实体单元C3D8R,锚栓、套筒均与锚固端板完全粘结,采用contact面面接触行为模拟锚固端板上部与混凝土的相互挤压作用,法向行为定义为硬接触,切向摩擦系数取0.3。根据已有的研究[8,9],锚固端板对抗拉承载力的贡献远大于套筒侧壁与混凝土间的粘结作用,因此忽略这种粘结作用,采用面面接触方式模拟。
约束混凝土块底面所有自由度,使用参考点耦合锚栓顶面,并施加竖向位移于参考点。锚固装置的有限元模型见图5。

图5 锚固装置的有限元模型
为保证上述计算的准确性,本文计算了文献[10]拉拔试验中的构件3,将数值模拟得到的荷载-位移曲线和试验曲线进行了比较,见图6所示。极限承载力试验值Nt=885.2 kN,模拟值Nc=920.3 kN,Nc/Nt=1.04。
从对比中可见,本文的计算方法与试验结果整体吻合较好,特别是在荷载较小的情况下,两条曲线基本重合,随着荷载的增大,两条曲线开始出现差异。这是因为,荷载较小的情况下混凝土处于线性状态,当荷载增大后混凝土开始开裂,表现出很强的非线性,使得数值模拟结果很难与试验情况完全对应。综合看来两者整体趋势相同,极限承载力结果接近,因此本文提出的计算方法是可行的。
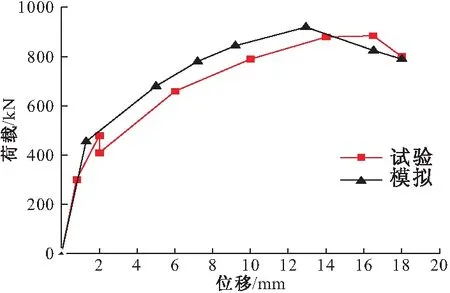
图6 计算曲线与试验曲线对比
2 计算结果分析
2.1 破坏模式
模型典型的破坏模式如图7所示,混凝土裂缝的发展如图8(图中“1000-350-68”表示埋深为1000 mm,锚固板边长为350 mm,套管外径为68 mm,下同)所示。由此可见,在锚栓受拉过程中,混凝土裂缝的发展主要分为两阶段,裂缝Ⅰ首先出现并大致沿着水平方向发展,随着拉力荷载逐渐增大,裂缝Ⅱ开始从锚固板边缘出现并沿与锚栓轴向一定的角度(60~65)斜向上发展,大致形成一个锥体破坏面,当裂缝Ⅱ出现后,裂缝Ⅰ的发展速度变缓,这与文献[11]中提到的现象相似。这是由于加载初期混凝土主要受锚固板的局部挤压作用,随着荷载的增加,混凝土受力模式向锥体破坏发展。
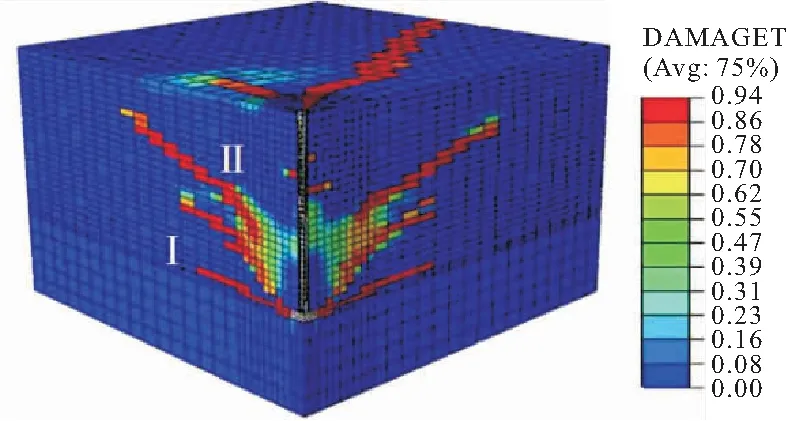
图7 破坏模式
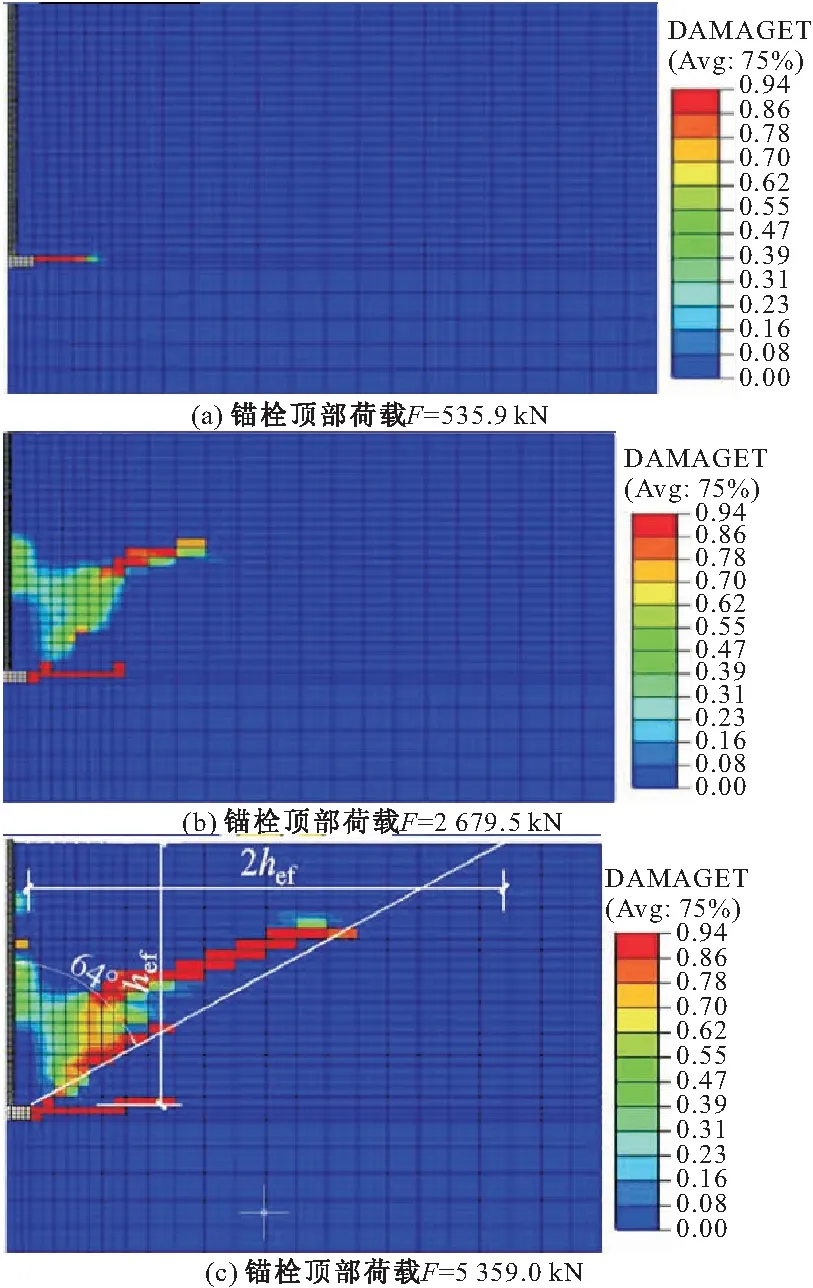
图8 混凝土裂缝发展(1000-350-68)
图9是锚栓底部某点位移与作用荷载的关系曲线,可以看出随着锚固端板与混凝土作用面积的增大,曲线峰值点对应的位移相应减少,这种趋势随着埋深的增加更为明显。
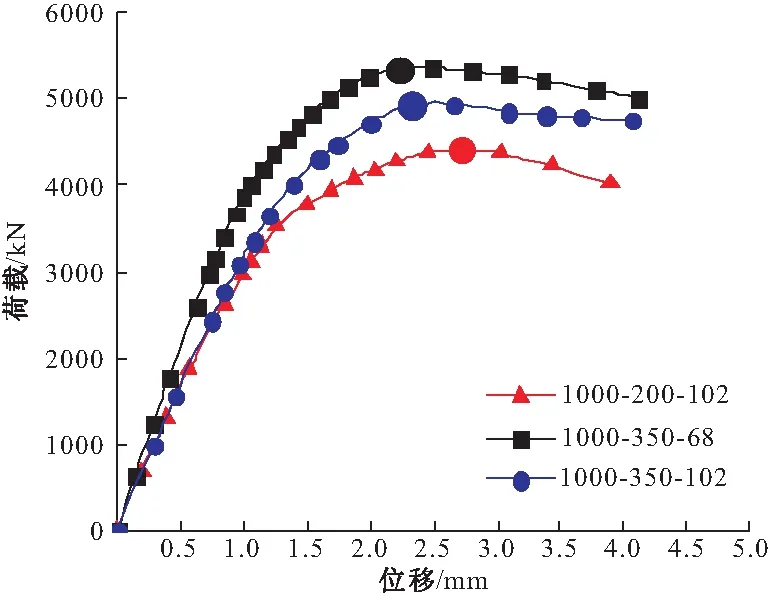
图9 典型的加载曲线
2.2 计算结果与现有理论结果对比
表2列出了本文计算的有限元模型的承载力以及采用CCD法与45CM法的预测承载力。
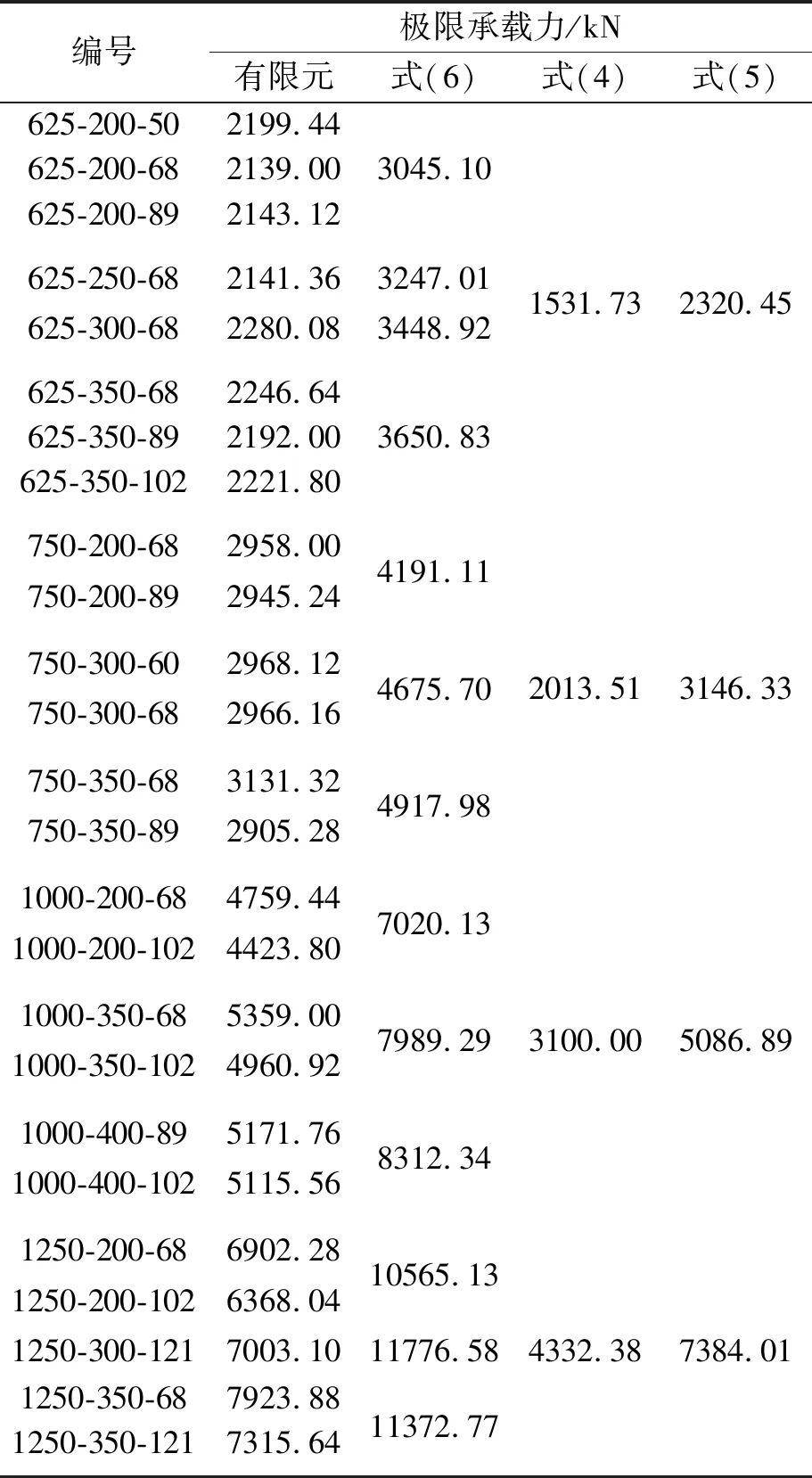
表2 构件承载力的模拟值与预测值
其中CCD法的计算公式见式(4),ACI 318-05对CCD法进行了补充,建议对于hef>280 mm的锚栓采用式(5)计算。45CM法的计算公式见式(6)。
(4)
(5)
(6)
式中:fcu为混凝土立方体抗压强度(MPa);hef为有效埋深(mm);dh为端头直径(mm),本文锚固板为正方形,因此按照等面积原则,取为边长的1.128倍。
图10a,10b分别表示使用有限元法计算的结构承载力Fc与CCD法中的式(4)(5)预测承载力Fpre的比值随锚栓埋深的变化。
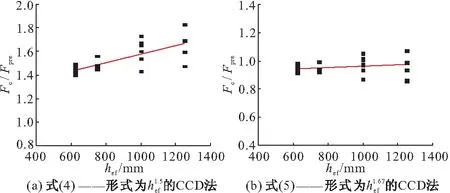
图10 模拟承载力与预测承载比值随埋深的变化
45CM法(式(6))认为承载力与hef2成比例,并且从表2的结果可以看出预测承载力均高于有限元计算结果,预测承载力大约为模拟承载力的1.5~1.7倍,显然使用式(6)会过高地估计结构的承载力,不能用于指导本装置的设计。CCD法中式(5)认为锚栓承载力与hef1.67成比例,从表2、图10b可以看出,整体上承载力模拟值小于预测值,两者的比值随着埋深的增大而略微增大,特别是对于hef≤750 mm的构件,有限元模拟值均小于预测值,因此采取这种方法用于设计是偏于不安全的。CCD法中式(4)认为锚栓承载力与hef1.5成比例,从图10a可以看出,这种方法计算的承载力均小于有限元模拟值,且Fc与Fpre的比值基本均在1.4之上,且两者的比值随着锚栓埋深的增大而增大,因此这种方法指导设计过于保守,特别是对于深埋构件。除此之外,式(4)(5)均没有考虑锚固端板尺寸的影响,从图10可以看出,随着埋深的增加,这种影响对于构件承载力的影响明显变大,并且本文中的锚固装置并不由单一带端板的锚栓组成,锚栓外套筒可能对承载力也有影响,这些都是式(4)~(6)所没有考虑到的,因此在现有理论基础上提出适合本装置的计算方法是必要的。
2.3 参数分析
2.3.1 埋深分析
为更好地研究锚固装置的埋深hef对其承载力的影响,对数据做以下处理:将表2中埋深≥750 mm模型对应的有限元计算承载力Fc分别除以与之相同锚固板边长、相同套筒直径、埋深为625 mm模型对应的承载力Fc(hef=625 mm),并对上述结果Fc/Fc(hef=625 mm)取对数作为纵坐标值,对与之对应的埋深hef取对数作为横坐标,如图11所示。
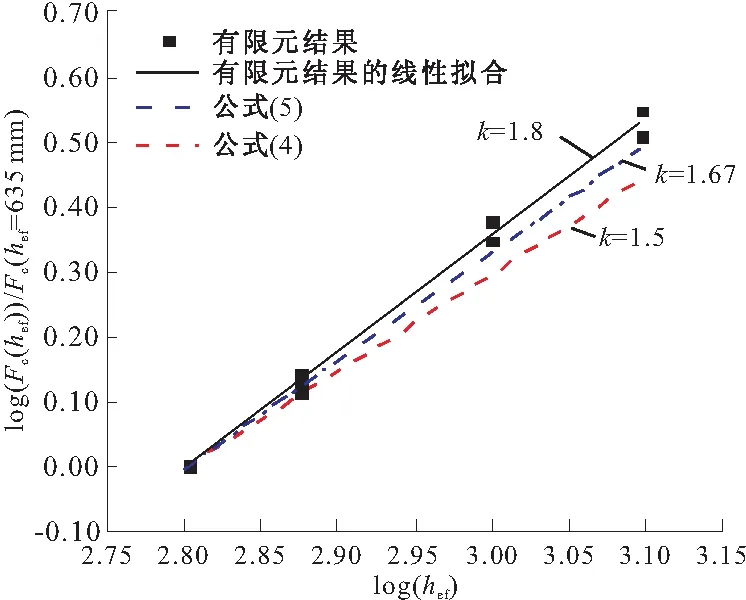
图11 hef对Fc的影响
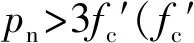
2.3.2 锚固端板及套筒尺寸分析
本文使用l/d来衡量端板及套筒尺寸的影响,基于2.3.1中埋深分析的结论与CCD法,认为承载力与fcu0.5hef1.8成比例,并对表2中数据做图12所示的处理,从图中可以看出,承载力与Fc与l/d的关系较为复杂,数据点分布较为分散,为了安全,承载力的取值采用图12中所示的下包线,即取偏下值。
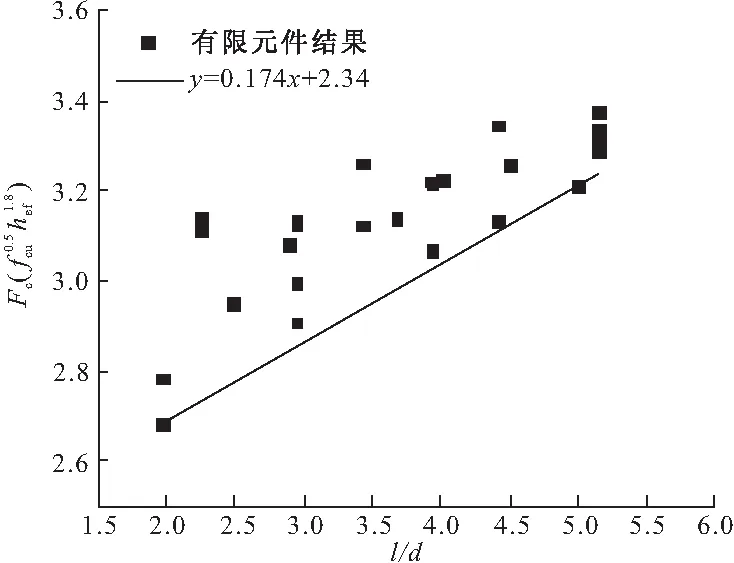
图12 l/d对Fc的影响
2.3.3 公式拟合
基于前文所述,发生混凝土锥体破坏时,保守地认为破坏锥体的半径为2hef+l/2,此时对应锥体倾角为64(见图8c),通过拟合数值计算结果得到锥体破坏下的计算式(7),将25个模型的计算结果与式(7)的拟合平面绘制于图13中,以l/d和hef为横坐标,以受拉承载力Fc为纵坐标。
(7)

图13 各数值点及式(7)对应的拟合平面
定义有限元结果得到的结果Fc及其与通过式(7)计算得到的Fc,p的比值为β,通过计算β的平均值为1.056,标准差为0.04。
2.4 锚固端板与锚杆的破坏分析
前文中模型均假定钢材为线弹性材料,因此不会发生钢材的屈服破坏,而实际中很可能出现钢构件的破坏先于混凝土的锥体破坏,导致结构最终的受拉承载力由钢构件的破坏所控制,因此有必要对锚固端板与锚杆的受力状态进行分析。
2.4.1 锚固端板分析
由于锚固端板处于复杂的空间受力状态,为了简化计算,如图14a,14b所示,假定锚固端板与混凝土接触面压力均匀分布,受拉锚栓直径为d′的圆形截面等效为边长为a的方形截面,其中a=0.8d′[13],将方形截面外的锚固端板沿虚线分为等大小的四部分,近似认为这四部分相互独立,每一部分可看作是一变截面悬挑梁,最大弯矩Mmax出现在端部,可按照图14c计算,q为锚固端板上的均布荷载,F为作用在锚栓上的拉拔力,q=F÷(l2-a2),则端部的最大正应力为:
σmax=Mmax/W
(8)
式中:W为截面抵抗矩。
最终得到锚固端板在力F的作用下最大正应力为:
(9)
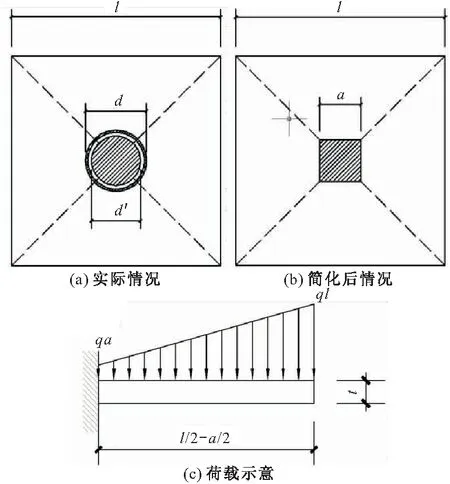
图14 锚固端板计算示意
为验证使用式(9)计算的正确性,以编号635-350-102模型为例对比分析公式计算结果与有限元计算结果。在F=100 kN时,式(9)的计算结果为199.66 MPa,有限元计算结果为187.02 MPa,如图15所示,可见式(9)可以较为准确地用来计算锚固端板的最大应力。
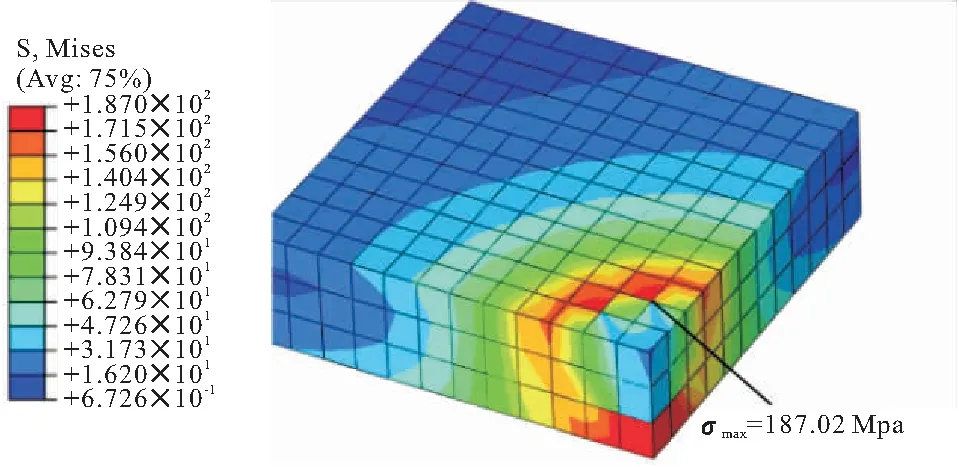
图15 锚固端板应力分布
不考虑截面的塑性发展,认为最大应力达到钢材的屈服应力为锚固端板所控制的承载力极限,则有:
σmax≤f
(10)
式中:f为钢材的抗弯强度设计值。
综合式(9)(10),可得由锚固端板控制的极限承载力Fp为:
(11)
2.4.2 锚栓分析
锚栓端部受拉力作用,认为锚栓的承载力是以截面的平均应力达到钢材的屈服应力为极限。锚栓的强度按式(12)计算:
(12)
式中:F为作用在锚栓上的拉拔力;A为锚栓的截面面积。
由此可得,由锚栓控制的极限承载力Fs为:
Fs=fA
(13)
因此综合考虑混凝土锥体破坏、锚固端板破坏、锚栓破坏三种破坏形式,锚栓套筒装置的抗拉承载力为Fc,Fp,Fs的较小值。
3 结 论
(1)本文针对振动台实际工程,提出了一种锚栓套筒装置,并对其锚固性能进行分析。计算发现,在保证钢材强度的情况下,锚固的破坏形式是装置周围混凝土的锥体破坏,同一埋深下,荷载-位移曲线中峰值点对应的位移随着锚固端板与混凝土接触面积的增大而增大。
(2)本文装置锚固端板尺寸较大且深埋于混凝土中,当基础尺寸大于4hef+l发生混凝土锥体破坏,现有的关于混凝土锥体破坏的设计公式不能很好地对应有限元计算结果,因此本文基于现有方法和数值拟合,提出了新的设计公式,修正了抗拉承载力与埋深的关系,并考虑了锚固端板与套筒尺寸的影响。
(3)除了混凝土锥体破坏外,本文还给出了锚固端板与锚栓单独破坏时的承载力计算方法,锚固装置最终的抗拉承载力为三种破坏形式分别对应承载力的较小者。

