在游戏体验中丰富数学思考
——《有余数的除法》教学案例(一)
王佳颖
【课前思考】
“有余数的除法”是表内除法知识的延伸和拓展。教材在内容的安排上,注重结合具体的情境将有余数的除法的意义内容置于实际生活的背景之下,加强对“余数”的意义理解。“有余数的除法”是以表内除法知识为基础进行学习的,学生虽然在实际生活中有一些感性的认识和经验,但缺乏清晰的认识和数学思考过程。
基于上述分析,设计本课教学时,笔者重点思考了这样一些问题:首先,如何激活并利用学生的已有经验展开教学,让课堂更加具有趣味性?其次,对于学生理解余数比除数小的道理大部分教学是在观察算式、分析、交流中发现到的,但是在这样的教学中,学生体会的仿佛不够深刻。如何将这个知识难点精准突破,让课堂有一种“课虽止而思未尽”的效果?
【教学过程】
一、课前游戏,激发兴趣
请8位学生上台做抱团游戏。游戏规则:其余的学生做裁判,齐喊“抱——抱——抱成团”,然后根据教师报出的数字,相应数量的学生抱在一起。
第一轮:教师报“2”。正好抱成4组,过关。
第二轮:教师报“4”。正好抱成2组,过关。
第三轮:教师报“3”。抱了2组,还剩2人。
师:出现了两种情况,一种是“正好”,还有一种是“有余”。今天我们就来研究数学中的“正好”和“有余”。(板书:正好 有余)
【思考:学生都喜欢玩游戏,这样可以提高课堂参与度,激发学生的学习兴趣,让课堂更加生动、热闹。在游戏中,引导学生直观理解“正好”和“有余”,寓教于乐。】
二、充分实践,感知意义
1.延续游戏。
用“小棒”继续玩“抱成团”的游戏。要求:(1)抱成团的小棒摆出一个图形;(2)想一想用哪个算式表示摆的过程。(两个学生上台摆,其他学生底下摆)游戏开始:“抱——抱——抱成团”,4。(有的学生拿到的是8根小棒,有的学生拿到的是9根小棒)

2.展示交流。
(1)关注摆法:以两位板演学生摆的作品为例,感受“正好”和“有余”。
(2)用算式表征“正好”:8根小棒,每4根摆1个正方形,正好可以摆2个正方形。怎样用算式来表示?[学生口答,教师板书:8÷4=2(个)]这个算式表示什么意思?每4根摆一个,8根里面正好有2个4根,也就是2个正方形。
(3)用算式表征“有余”:9根小棒,每4根摆1个正方形,摆了2个正方形,还余1根。像这种情况,又该怎样用算式表示呢?试一试,写在纸上。(学生尝试,教师巡视,并选取代表性作品展评)
3.感知范例。
(1)认识“余数”:同学们说的都很有道理。“有余”的情况,如果用除法来表示的话,就像刚才第三位同学想的那样,这里的“1根”就叫做余数。[板书:9÷4=2(个)……1(根)]
(2)结合摆出的图形,说说算式的意义,认识各部分的名称。
师:这就是“有余数的除法”,也是今天要重点学习的内容。
【思考:开课游戏继续延伸,学习热情得以保持。具体地说,把“学生抱成团”转化成“小棒抱成团”,组织学生经历“摆小棒”“写算式”的过程,让学生进一步体会“正好”和“有余”,从中认识了“余数”及“有余数的除法”。这个过程将学生的所想所做暴露在课堂现场,体现了“学为中心”的教学理念。同时,在自由创作、观察比较、表达发现的经历中,切实发展了学生的实践能力与推理素养。】
三、反复实践,探寻关联
1.研究“11根小棒摆正方形”。
师:大家都是正好摆了2个正方形,还余1根小棒。有不一样的情况吗?(学生回答:摆了2个正方形,还余3根小棒)请大家想想,他一共有几根小棒?为什么?[学生口答,教师板书:11÷4=2(个)……3(根)]看来 9根小棒摆正方形“有余”,11根小棒摆正方形也“有余”,都不能“抱成团”。
2.想想“10根小棒摆正方形”。
师:如果是10根小棒摆正方形,请你想象着摆图形,并写出算式。[学生口答,教师板书10÷4=2(个)……2(根)]摆了几个正方形?余几根?
3.推算“12至16根小棒摆正方形”。
师:如果总数再加1根,4根4根抱成团,能摆几个正方形?余几根?余4根可以吗?再增加小棒继续摆,你能推算出结果吗?
4.观察对比,发现“余数和除数的关系”。
(1)观察:仔细观察这些除法算式,你发现了什么?
(2)质疑:为什么余数总是1、2、3 而不是其他的数?
(3)猜想并验证:余数可能是4或5吗?为什么?
(4)归纳:余数既不能比4大,也不能和4相等。余数必须比除数小。(板书:余数<除数)
【思考:上述活动中,“数形结合”是极为重要的思想拐棍。并且,此处的“形”并非常规的“表象直观”,而是一种逐层递进的“思维图景”。从“实物摆小棒”的“形”到“脑中想小棒”的“形”,生动彰显了思维锤炼的层次性与达成度。有了“形”的支撑,学生对“数”(算式)的意义理解得以不断深入、扎实建构。与此同时,“余数与除法的关系”也已经“呼之欲出”。】
四、巩固运用,加深理解
1.猜一猜。
师:老师用一堆小棒摆五边形,想一想,如果有剩余,可能会剩几根?
师:为什么只有这几种可能性?说说你的理由。
师:如果摆三角形,可能会剩几根?
【思考:从“正方形”到“五边形”,实现了学习材料的变式,有利于凸显“有余数的除法”思维模式的广泛性与一般化。】
2.闯关游戏。
第一关:
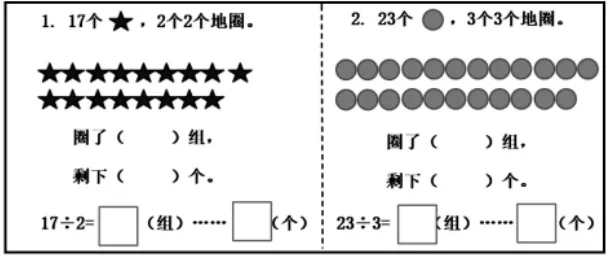
第二关:

第三关:
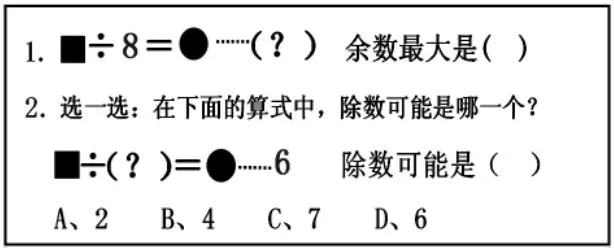
3.机动练习。
师:继续“8个同学抱成团”的游戏,如果要有剩余,想一想,除数不可能是几?可能是几?
8÷( )=( )……( )
【思考:开展生动活泼的课堂活动,教师不该忽视一个重要问题“学生学会了吗?”显然,达成度是数学教学最为基本的价值视点。为此,在课堂巩固阶段,笔者设计了富有挑战性的“闯关游戏”,引导学生在充满激情的问题解决中,真实呈现学习收获及客观疑难,进一步夯实了课时目标的达成度。】
【课后反思】
如果要用简洁的语言来概括本课的特点,那就是“动静相宜显效果”“逐层递进促发展”。首先,动静相宜显效果。很多数学课内容简单,但课堂设计不够吸引学生,导致学生参与度不高,教学效果一般。本节课的课前游戏环节,让课堂更加活泼且具有趣味性。学生通过玩游戏、摆一摆小棒,将抽象的算式转化成具体的图形,学生会感受到“原来数学课还可以这么有味道”,学生玩着、笑着就深刻地学习了知识。当然,全课不仅关注必须的“动”,更重视必要的“静”。比如,学生不仅“依托图形说算式”,又“根据算式想图形”,真正体会到了“数形结合”的好处。其次,逐层递进促发展。反观整节课,既基于直观,又有序抽象,切实帮助学生形成了对“余数”“有余数的除法”的概念认知,建立了“余数比除数小”的逻辑关联,真正促进了全体学生的数学发展。

