2020年高考解三角形考点预测
罗文军
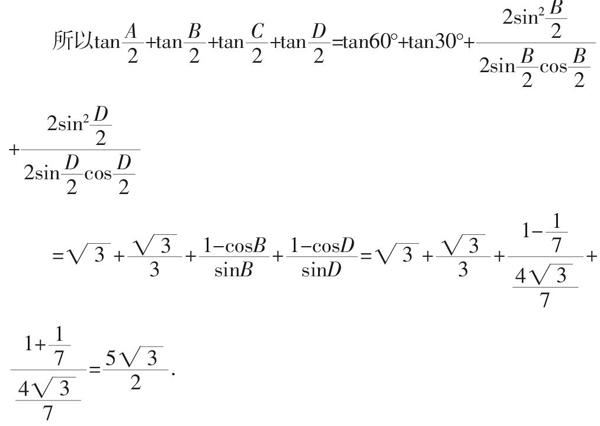
从近年高考真题来看,解三角形的考查在全国Ⅰ卷通常以解答题的形式出现在第17题,从考查内容上来看,以考查正弦定理、余弦定理、三角形的面积公式为主,通常与三角恒等变换和不等式交汇来考查,从考查的思想方法上来看,主要考查化归与转化、函数与方程和数形结合的思想,从考查的能力上来看,主要考查运算求解能力、推理论证能力,旨在考查考生的逻辑推理和数学运算的数学学科核心素养. 本文通过预测2020高考解三角形的核心考点,以期帮助同学们更高效地备考.
一、以四边形为载体,考查解三角形
这类试题从考查知识点来看,以四边形为载体,考查余弦定理、三角形面积公式和三角恒等变换,考查化归与转化和方程的思想,考查应用意识.
例1. 四边形ABCD的内角A与C互补,AB=2,BC=6,AD=CD=4.
(1)求A和BD;
(2)求四边形ABCD的面积和 tan■+tan■+tan■+tan■的值.
解析:(1)由题设及余弦定理得,
BD2= AB2+AD2-2AB·ADcosA=20-16cosA……①
BD2= BC2+CD2-2BC·CDcosC=52+48cosA……②
由①②得cosA=-■,故A=120°,BD=2■.
(2)四边形ABCD 的面积为:
S=■AB·AD sinA+■BC·CD sinC
=(■×2×4+■×6×4)sin120°=8■,
由题设及余弦定理得:
AC2=AB2+BC2-2AB·BCcosB=40-24cosB……(Ⅰ)
AC2=AD2+CD2-2AD·CDcosD=32+32cosB……(Ⅱ)
由(Ⅰ)(Ⅱ),得cosB=■,cosD=cos(B)=-cosB=-■.
因为0
所以sinD=sin(B)=sinB=■,
所以tan■+tan■+tan■+tan■=tan60°+tan30°+■+■
=■+■+■+■=■+■+■+■=■.
【评注】破解本题第(1)问先分别在对角线分成的两个三角形中利用余弦定理列出式子,根据诱导公式,代入已知条件,解方程组得出角A和对角线BD的值;第(2)问要把求四边形ABCD的面积问题化归求△ABD和△CBD的面积之和,结合三角形面积公式解之可得,求tan■+tan■+tan■+tan■的值,连另一条对角线AC,在AC分四边形ABCD所得的△BAC和△DAC中,分别利用余弦定理列出式子,解方程組得出cosB的值,运用诱导公式得出cosD的值,再由平方关系式得出sinB的值,再运用商式关系和二倍角的正弦公式、余弦公式计算可得.
二、三角形面积的最大值问题
这类试题通常第(1)问考查利用正弦定理或余弦定理解三角形,第(2)问三角形的面积的最大值问题,考查余弦定理、三角形面积公式和重要不等式,考查了化归与转化的思想,考查推理论证能力和运算求解能力,旨在考查考生的逻辑推理和数学运算的核心素养.
例2. △ABC的内角A, B, C的对边分别为a, b, c,已知3ccosB=(5a-3b)cosC.
(1)求sinC;
(2)若c=2,求△ABC的面积的最大值.
解析:(1)解法1:由正弦定理及已知得:
3sinCcosB=(5sinA-3sinB)cosC,
3(sinBcosC+cosBsinC)=5sinAcosC,
3sin(B+C)=5sinAcosC,
3sin(A)=5sinAcosC,3sinA=5sinAcosC.
因为0 所以cosC=■. 因为0 解法2: 由余弦定理可得: 3c·■=(5a-3b)·■, 所以■=■-■, 3a=■,所以a2+b2-c2=■ab. 由余弦定理,可得cosC=■=■=■,因为0 所以sinC=■=■. (2)由已知及余弦定理,得4=a2+b2-2abcosC=a2+b2-■ab, 由重要不等式,可得a2+b2≥2ab,故4≥2ab-■ab,ab≤5, 当且仅当a=b时,ab取得最大值5, △ABC的面积的最大值为S=■absinC=■ab=2. 【评注】第(1)问解法1是利用正弦定理化边为角后结合三角形内角和定理与三角恒等变换进行转化,得出cosC的值,再运用平方关系式得出 sinC的值;第(1)问解法2是利用余弦定理推论化为边的关系,整理后通过观察发现右边有项和左边分母相同,移项化简,再结合余弦定理推论和整体代换思想得出cosC的值,同解法1可得sinC的值;第(2)问运用余弦定理得出关于a和b边的等式,运用重要不等式将等式放缩为不等式,解得ab的最大值,再运用三角形面积公式可得△ABC的面积最大值. 三、与边有关的最值问题 这类题型第(1)问通常考查正余弦定理的应用,第(2)考查正弦定理和三角恒等变换以及三角函数的最值问题,考查化归与转化的思想和函数与方程的思想. 例3. △ABC的内角A, B, C的对边分别为a, b, c,设(sinA-sinB)2 = sin2C-sinAsinB. (1)求角C;
(2)若AB=■,求AC+2BC的最大值.
解析:(1)因为 sin2A+sin2B-sin2C=sinAsinB,
由正弦定理,可得 a2+b2-c2=ab,
由余弦定理,可得cosC=■=■=■,
因为0 (2)由余弦定理,可得■=■=■=■=2, 所以AC=2sinB,BC=2sinA, AC+2BC=2sinB+4sinA=4sinA+2sin[?仔-(A+■)] =4sinA+2sin(A+■)=4sinA+2(■sinA+■cosA)=5sinA+■cosA=2■sin(A+?渍),其中cos?渍=■,sin?渍=■. 因为0 【评注】第(1)问先运用正弦定理实现角化边,再运用余弦定理推论和整体代换的思想得出角C的余弦值,从而得出角C;第(1)问运用正弦定理实现边化角,应用三角形内角和定理和三角函数诱导公式转化成求关于角A的三角函数在给定范围上的值域问题,运用辅助角公式可得出最大值. 四、三角形的周长问题 这类解三角形中的求三角形周长的问题,通常考查正弦定理、余弦定理和三角形面积公式,也有时运到完全平方式. 例4. 在△ABC中,角A, B, C所对边分别为a, b, c,且■+■=■. (1)求 ■ 的值; (2)若△ABC的面积S=■,△ABC的外接圆的直径为2,求△ABC的周长. 解析:(1)由正弦定理和已知可得,■+■=■=1, 所以■=1, 所以■=1,所以■=1,所以■=1. (2)由正弦定理,得■=■,所以b=■, 所以S=■absinC=■a2■=■a2=■,所以a=1. 由正弦定理,可得■=■=2R=2,所以sinA=■,所以A=■. 由三角形面积公式,得S =■bcsinA=■bc=■,所以bc=2, 由余弦定理,可得a2=b2+c2-2bccosA,1= b2+c2-■bc. 所以(b+c)2-(2+■)bc=1,所以b+c=■, 所以△ABC的周长为1+■. 【评注】本题第(1)问借助正弦定理实现边化角,再运用三角恒等变化中的两角和的正弦公式,再运用三角形内角和定理和三角函数诱导公式可求出■ 的值;第(2)问先运用正弦定理和三角形面积公式可求出边a和角A的值,再运用三角形面积公式可得出bc的值,運用余弦定理和完全平方式可得出b+c的值,从而求出△ABC的周长值. 五、解三角形问题与三角恒等变换的综合问题 解三角形问题与三角恒等变换问题的综合问题,也是高考命题的一个热点问题. 例5. △ABC的内角A, B, C的对边分别为a, b, c,满足4S△ABC =■(a2+b2-c2). (1)求角C 的大小; (2)已知cos(B+■)=■,求cos2A的值. 解析:(1)由三角形面积公式及已知可得: 2absinC=■(a2+b2-c2). 由余弦定理,可得c2=a2+b2-2abcosC,所以2abcosC=a2+b2-c2, 所以2absinC =2■abcosC,所以tanC=■. 因为0 (2)令t=B+■,则B=t-■,cost=■, 由 B∈(0,■),则 t=B+■∈(■,■), 所以sint=■=■=■, 所以sin2t=2sintcost=2×■×■=■, cos2t=cos2t-sin2t=■-■=■, 所以cos2A=cos[2-B-C)]=cos(2B+2C)=cos[2(t-■)+■] =cos(2t+■)=cos2tcos■-sin2tsin■=■. 【评注】第(1)问要借助三角形面积公式、余弦定理和三角函数的商式关系可得出角C的正切值,从而得出角C 的大小;第(2)问换元后,根据三角形内角和定理得出B的范围,从而得出角t的范围,再运用平方关系式得出sint的值,再运用二倍角公式得出sin2t 和cos2t 的值,再运用三角形内角和定理、三角函数诱导公式和三角恒等变换可得出cos2A的值. 六、三角形的内切圆半径问题 这类问题,先要根据已知条件,通过解三角形得出三角形的所有边长和面积,再根据三角形的内切圆半径等于三角形面积的二倍除以三角形的周长可破解. 例6. △ABC的内角A, B, C所对的边分别为a, b, c,已知sin2B-2cos2■=■. (1)求B 的大小; (2)若b=3■,a+c=9,求△ABC的内切圆的半径. 解析:(1)由sin2B-2cos2 ■=■, 得4sin2B-8cos2■=1, 得4sin2B-8cos2(■-■)=1,得4sin2B-8sin2■=1, 4(1-cos2B)-8×■=1, 整理,可得4cos2B-4cosB+1=0, 所以cosB=■,因为0 (2)由余弦定理可知: b2=a2+c2-2accosB,b2=(a+c)2-2ac(1+cosB), 所以(3■)2=92-2ac(1+■),得ac=18.
由三角形面积公式S△ABC=■acsinB=■×18×■=■,
记△ABC的内切圆半径为r,
则 ■(a+b+c)r=S△ABC,所以r=■=■=■=■.
【评注】第(1)问根据三角形内角和定理、三角函数诱导公式、同角三角函数平方关系式和降幂扩角公式可得出关于cosB的一元二次方程,根据三角形内角B 的范围可得出角B 的值;第(2)问根据余弦定理和完全平方公式可得出ac的值,再运用三角形面积公式可得出△ABC的面积,再运用等面积法可求出△ABC的内切圆半径公式.
七、解三角形中的数学文化问题
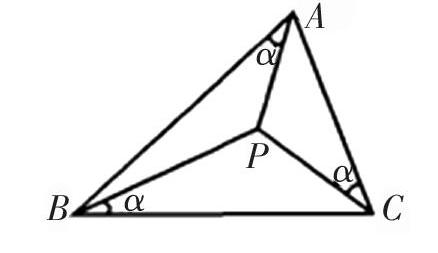
例7. 勃罗卡是法国著名的数学家,已知三角形△ABC中,P是其内部一点,如果∠PAB=∠PBC=∠PCA= ?琢,则称?琢为勃罗卡角,点P称做勃罗卡点(如图所示)
已知如图△ABC的内角A, B, C的对边分别为a, b, c,且a=3,b=7,c=5,
(1)求△ABC的面积;
(2)求△ABC的勃罗卡角a 的余弦值cosa.
解析:(1)在△ABC中,由余弦定理可得:
cos∠ABC=■=■=-■,
因为0<∠ABC<,所以∠ABC=120°,
所以S△ABC =■acsin∠ABC=■×3×5×■=■.
(2)设PA=x,PB=y,PC=z,
由三角形面积公式可得:
S△ABP =■cxsin=■xsin,
S△BCP =■aysin=■ysin,
S△CAP =■bzsin=■zsin,
由上可得,(5x+3y+7z)sin=2(S△ABP +S△BCP +S△CAP)=2S△ABC ,
所以(5x+3y+7z)sin=■……①
分别在△ABP、△BCP、△CAP中运用余弦定理可得:
y2=52+x2-10xcos,
z2=32+y2-6ycos,
x2=72+z2-14zcos,
将以上三式相加可得:
(5x+3y+7z)co=■×(52+32+72),
即(5x+3y+7z)cos=■……②
①式和②式两边平方相加可得:
(5x+3y+7z)2=1891,5x+3y+7z=■,
cos=■=■.
【評注】本题是一道给出背景的显性数学试题,取材于著名的数学名题勃罗卡点问题. 第(1)问根据余弦定理和三角形面积公式可求出三角形△ABC的问题;第(2)问先根据三角形面积公式可得出△ABP、△BCP、△CAP 的面积,再相加整理可得出①式,再分别在△ABP、△BCP、△CAP 中运用余弦定理,相加可得出②式,再把①和②平方相加整理可得出勃罗卡角?琢的余弦值cos?
责任编辑 徐国坚

