双重向量积展开法则的两种证明方法*

马宝林，李 帆

(河南科技学院 数学科学院，河南 新乡 453003)

双重向量积运算是解析几何中的重要内容，其展开法则更是向量代数的重点与难点.文献[1]中对双重向量积展开法则的证明是利用线性相关性化将一般形式化为特殊形式的方法进行，证明过程繁琐，套用结论较多，学生理解困难.文献[2]利用坐标法给出证明，较文献[1]简单，但逻辑性太强，只适用于程度较好的学生.文献[3]的证明比较特殊，相对比较直观简单，但证明过程不够完整.本文在以上文献的基础上，给出两种更为一般的证明方法，且通过课堂实践发现教学效果更佳.

1 预备知识

定义1[1]59给定空间三向量，先作其中两个向量的向量积，再作所得向量与第三个向量的向量积，那么最后的结果仍然是一个向量，叫做所给的三个向量的双重向量积.

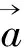
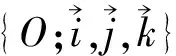
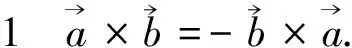
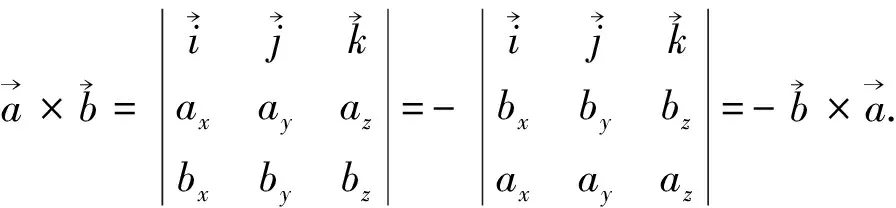
2 双重向量积展开法则

(*)

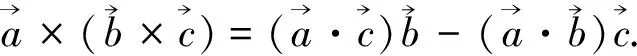
依据引理2可知，

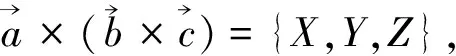
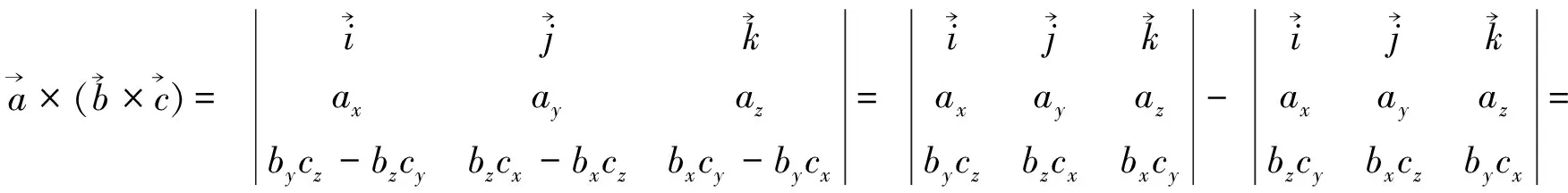
将二阶行列式展开有

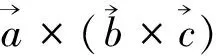
X=aybxcy-aybycx-azbzcx+azbxcz=(aycy+azcz)bx-(ayby+azbz)cx

同理可得

所以，(*)成立，定理得证.

该证明方法依据双重向量积与三阶行列式的对应关系而进行，关键点在于行列式的展开与项的合并，最后利用加项减项凑得数量积的运算.思路清晰，过程简单，利于学生独立完成证明.

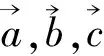
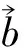
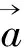
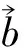
由引理2得

依据内积的定义可知，

所以，(*)成立.

该证明方法利用将三个向量置于直角标架的特殊位置后产生的特殊坐标而进行，关键点在于向量坐标的特殊性以及内积的定义，等式两端左右开弓，形成结论.运算简单，逻辑清晰，更有利于学生发散性思维的培养.

(**)

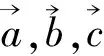
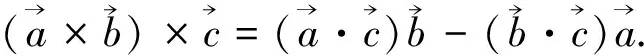
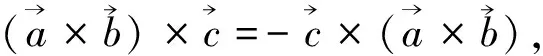
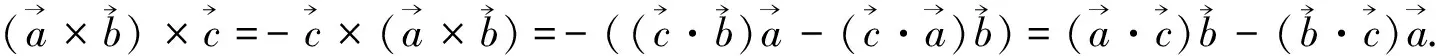
3 结语

三向量的双重向量积是解析几何中的一个重要内容，其应用也非常广泛，特别在向量代数、恒等式证明和基本图形的位置关系以及公垂线方程的求解等方面有着重要的应用，本文的两种证明方法更为一般化，第一种适合运算能力较强的学生，第二种适合逻辑能力较强的学生，二者具有互补作用，为学习解析几何与相关专业研究提供参考.