勒贝格积分与黎曼积分的关系*
张永立 ,黄 芳 ,王学军 ,范志勇
(1焦作师范高等专科学校 数学学院, 河南 焦作 464000;2山西大学 计算机与信息技术学院 ,山西 太原 030000)
黎曼积分[1-2](下文简称“R积分”) 和勒贝格积分[3-4](下文简称“L积分”)是近代分析数学的最基本概念之一,L积分是想克服R积分的一些缺陷,使得微分与积分的运算更加完善,但他们之间既有区别又有联系.Corporation H P[5],Henstock R[6]等分别从不同的角度阐述了这两种积分的联系与区别. 近年来,国内一些学者也从不同的视角比较了两种积分的优劣[7-10],那么,仅从函数的范围来看,L积分要比R积分广泛得多,同时L积分也比R积分优越许多,利用L积分来研究R积分的许多概念,可以得到许多更深刻的结果,提出了R积分本身无法解决的一些问题的理论依据.
本文从积分的定义出发,对可积的充要条件、可积函数的连续性、积分的可加性、积分极限定理以及两种积分的区别与联系进行了比较,同时对鲁津定理做了一个小推论,并证明了该推论,说明了L可积函数是R可积的条件.
1 预备知识
1.1 R积分的定义
设f(x)在[a,b]上有界,T表示[a,b]上的任一分划
a=x0 将区间[a,b]分成n个小区间,设Mi,mi分别是f(x)在每个小区间[xi-1,xi]上的上、下确界, 则称f(x)在[a,b]上R可积,记为 设f(x)是可测集E⊂Rq(mE<∞)上的有界勒贝格可测函数,对于可测集E的任一分划T={E1,E2,…,En},记 f(x)在可测集E上的上、下积分分别为 如果 则称它为f(x)在E上关于勒贝格测度的积分,即L积分,记作 我们知道Dirichler函数 定理1 函数f(x)在[a,b]上的有界函数,则函数f(x)在[a,b]上黎曼可积的充要条件是f(x)在[a,b]上不连续点集构成一个零测度集. 定理2 设f(x)是可测集E⊂R(m(E)<∞)上的有界函数,则f(x)在E上勒贝格可积的充要条件是f(x)在E上勒贝格可测. 定理1告诉我们,对于区间[a,b]上的有界函数,其黎曼可积性并非由该函数在不连续点处的状态所致,而是取决于他的不连续点集的测度. 事实上,对于仅仅在所有的无理点是连续,但在所有的有理点不连续的黎曼函数 同时,定理2表明对于Rq中测度有限的可测集上的有界函数可测和勒贝格可积是同一回事. 现在再来看R可积与L可积具有什么样的性质. 定理3 设f(x)是定义在集合E上的连续R可积函数,则对任意的δ>0,存在闭子集Eδ⊂E,使f(x)在Eδ是连续函数,且 m(EEδ)=0. 定理4 设f(x)是可测集E上几乎处处有限的可测函数,则对任意的δ>0,存在闭子集Eδ⊂E,使f(x)在Eδ是连续函数,且 m(EEδ)<δ. 定理3表明,对于黎曼可积函数的情形,在集合E⊂Rn上,若有界函数f(x)最多有有限个间断点,则函数f(x)为一个几乎处处连续的函数.同时,如果一个函数是几乎处处连续的,那么这个函数就几乎处处等于一个连续函数,即是说它也是E⊂Rn上的可测函数. 定理4表明,几乎处处可测的函数是“基本上连续”的函数. 从而由定理3和定理4我们可以知道黎曼可积函数是几乎处处连续,勒贝格可积函数是“基本上连续”的函数,故黎曼可积函数必是勒贝格可积函数. 由于黎曼可积函数是建立在约当测度的基础之上,那么由定理5,对于黎曼可积函数的情形只有有限可加性.反观建立在勒贝格测度之上的勒贝格积分,具有可数可加性,克服了黎曼积分一些缺陷。 定理7 若函数列{fn(x)}在E上一致收敛,且每一项都连续,则 定理8 设 (1){fn(x)}是可测集E上的可测函数列; (2)|fn(x)|≤F(x)几乎处处于E,n=1,2,…,且F(x)在E上可积,称{fn(x)}为F(x)所控制,而F(x)叫做控制函数; (3)fn(x)⟹F(x),则f(x)在E上可积,且 定理7给出了黎曼积分与极限交换的条件,要求被积函数必须一致收敛,此条件限制极强,不仅使得条件的检验不方便,而且运算难度大. 定理8表明了勒贝格积分与极限交换的条件,要求存在控制函数F(x),且使得|f(x)| 比较定理8和定理9,我们不难发现黎曼可积的积分与极限的交换条件较为严格,但是勒贝格积分的交换条件较弱,相较而言具有一定优越性。 定理9 设f(x)在[a,b]上R可积,则它必同时L可积,且有相同的积分值 另一方面,却存在有R不可积,但却L可积的函数,例如我们已经提到过的Dirichler函数就是R不可积,但它却是L可积的. 但值得注意的是,我们知道L可积是一种绝对收敛积分,而R反常积分不一定绝对收敛,可见L积分是R积分的推广但却不是R反常积分的推广. 那么,具备什么样性质的L可积函数类是R可积的.我们借助鲁津定理来证明如下定理. 定理10 设E⊂Rn,f(x)是E上a.e有限的可测函数,则对任意的δ>0,存在闭子集F和Rn上的连续函数g(x),使得: (1)m({x∈E:f(x)≠g(x)})<δ; (2)f(x)为F上几乎处处连续的函数. 证明 据鲁津定理,f(x)是E上a.e有限的可测函数,则对任意δ>0,存在闭子集Fδ⊂E与Rn上的连续函数g(x),使得m(EFδ)<δ,且f(x)=g(x),x∈Fδ,又({x∈E:f(x)≠g(x)})⊂m(EFδ),从而: m({x∈E:f(x)≠g(x)})<δ. (1)式得证,为了达到证明(2)式的目的,我们构造Rn上的连续函数列gn(x),使得当x∈Fδ时,有gn(x)=f(x).所以对任意的η>0,有 E[|f-gn|≥η]⊂EFδ, 由此即得 mE[|f-fn|≥η]≤m(EFδ)<δ, 因此 注:1).我们的定理10建立在鲁津定理的基础之上,因此可以看成是鲁津定理的推论; 2).我们知道R可积必L可积,但L可积不R可积,定理10给出了L可积函数是R可积的条件. 我们知道,若f(x)是R可积的,则|f(x)|也R可积,但若|f(x)|R可积,那么f(x)不一定R可积,相反,对于L可积而言,若函数f(x)在集合E上可测,函数f(x)是L可积的充分必要条件是|f(x)|是L可积的. 无论是可积的充要条件、可积函数的连续性、可加性、积分极限定理还是二重积分化成累次积分的计算,黎曼积分的条件都是比较严苛的,运算复杂,条件验证难度大,然而,勒贝格可积条件宽松易于验证,运算复杂度低等特点,同时黎曼积分中的一些结论也必须借助于勒贝格积分才能得到,用L积分可以解决R积分中比较困难的问题,这也是我们以后研究的一个方向.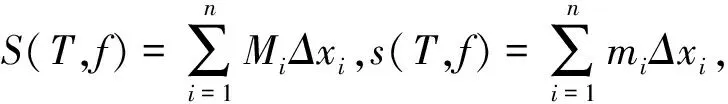


1.2 勒贝格积分的定义

1.3 两种积分定义的比较

2 主要的区别与联系
2.1 R可积与L可积的充要条件

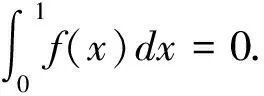
2.2 可积函数的连续性
2.3 积分的可加性


2.4 积分极限定理
3 结论
3.1 L积分与R积分的关系

3.2 L积分优点与R积分的缺点


