基于数学建模思想的高等数学案例教学研究*

宋长明，张建林

(中原工学院 理学院，河南 郑州 450007)

习近平总书记在全国教育大会上指出，培养什么人是教育的首要问题，并强调要在增强学生综合素质上下功夫。教育部在《关于加快建设高水平本科教育 全面提高人才培养能力的意见》中指出：要坚持学生中心，全面发展，激发学生学习兴趣和潜能，增强学生的创新精神和实践能力。教育部部长陈宝生提出“要着力推动课堂革命”，课堂革命可以看作是大学数学改革的深化，而课堂革命必须落实在每一门课堂教学中去才具有现实意义[1]。因而，有必要在高等数学课程中融入数学建模思想[2- 4]，将高等数学与专业知识相结合，从而改革课堂教学内容，进一步激发学生的学习兴趣，培养学生自主学习的习惯，提高课堂教学质量，更有利于培养学生的综合素质、创新能力和实践能力[5]，进一步提升人才培养质量。目前，随着高新技术产业的兴起，加上对于环境保护的考虑，对利用高新技术开发纺织品，也提出了更高的要求，而纺织学科与其他工程学科的联系日益紧密，因此进一步提升纺织专业的人才培养质量，有利于服务社会经济发展。

一、以纺织科学与工程专业为例，看数学建模思想

数学建模的思想主要体现在运用数学知识、技能和方法解决实际生活中遇到的问题。对实际问题进行建模的主要思路是：1) 用精炼的数学语言把实际问题化简为数学问题；2)通过建立数学模型并进行求解，来获得相应实际问题的解决方案。以纺织学科为例，近年来，数学建模在纺织科学与工程研究方面得到了广泛的应用，已经成为人们从事生产实践的重要手段之一。在纺织配棉方面，将线性规划模型用于配棉方案和设计洗呢工艺的优化，将线性回归方法用于描述纱线的品质与支数之间的数量关系，将层次分析法用于纺纱工艺配置方案的优化，将人工神经网络用于预测成纱质量[6]；在纺丝设计方面，将流体力学、空气动力学、气泡动力学等交汇融合，设计新的纺丝工艺——气泡静电纺丝，这成为生产纳米纤维的重要方法[7]；根据纺织品的多孔介质特性，采用“平行圆柱孔”结构特征的纺织热湿传递模型，预测设计效果、形状和功能等[8]；通过研究织物的起毛起球过程的特征模式，并结合主要的影响因素，构建相应的数学模型，从而研究织物起球质量的变化趋势[9]；在纺织品纹样设计方面，利用分形数学模型，对面料纹理的图像进行分析，进一步构建新的公式、配制着色方案以及调整相关公式参数，再创作生成分形艺术品[10]；将微生物对水中污染物降解过程进行数学表达，构建相应的数学模型，揭示这些生物化学反应的基本规律，这不仅有助于对污水生物处理原理的深入理解，而且是优化设计和运行条件的有效工具[11]。

高等数学作为理工科学生的重要公共必修课，随着科技信息技术的飞速发展，要求施教者在教学内容和体系上必须有所创新。在高等数学教学过程中融入建模思想和方法，对培养学生的学习兴趣和解决实际问题的能力，以及进一步拓展学生的学习思维有着非常重要的意义。然而，在实际教学中，融入数学建模思想的精髓需要任课教师下一番功夫。原因在于数学建模往往与具体的问题和方法紧密相连，如何将实际问题中的数学原理抽象出来，使得它既能激发学生的学习兴趣，又能将与所学专业的相关案例融入高等数学教学中，这将成为施教者所面临的重要问题[12]。

二、基于数学建模思想的高等数学案例

以实际问题为导向，尤其是以所学专业中的实际问题为导向，是目前高校教学改革的一个重要方向。在对基础理论知识的讲述中，要积极采用以学生为主体的启发式教学方式，设计一系列问题促使学生思考，使他们拓展思路[13]。下面以纺织科学与工程专业为例，探讨将建模思想融入到高等数学教学的案例。

(一)案例一：函数极限问题

在函数极限教学中，发现学生对函数极限的概念和求解比较难掌握。高等数学课程中在描述函数极限时，主要分为两种情形：一种是自变量趋于无穷大时函数的变化趋势，另一种是自变量趋于有限值时函数的变化趋势。对纺织专业学生的实际教学中，可以选取纺织印染废水生物处理方面的案例对此部分进行分析讲解。例如，微生物的生长速度和底物的浓度之间存在下列关系式[14]：

(1)

其中μ为微生物的生长速度，μmax为微生物的最大生长速度，x为底物的浓度，k为半饱和常数。当x→∞时，μ→μmax，此时该反应相对于底物是零级反应，增加底物浓度不能提高反应速度；当x→0，μ→0，此时反应相对于底物是一级反应，增加底物浓度可以提高反应速度。

在实际教学中，引入此案例，并结合图形，利用专业术语数学思想来解释，使学生了解了函数的变化趋势，学会了函数极限的计算方法，并且体会解决这类专业问题时所用到的极限的思想与精髓。

(二)案例二：定积分问题

在定积分的实际教学过程中发现大多学生较难掌控，主要体现在不会应用定积分解决实际问题以及后续学习中不理解多重积分的概念。在对纺织专业学生的实际教学中，可以选取纺织科学方面的实际问题对此部分进行分析，具体案例如下：

(水污染问题)某纺织印染工厂排出大量废水，造成了严重的水污染问题，于是工厂通过减产来控制废水的排放量。若第t年废水的排放量为C(t)(为连续函数)，则该厂在t=0到t=5年间排出的总废水量是多少？

模型假设：由于C(t)为连续函数，故在很小的时间区间上，C(t)可以近似地看做一常量，把区间[0,5]细分为n个小区间[ti-1,ti]，Δti=ti-ti-1,i=1,2,…,n。

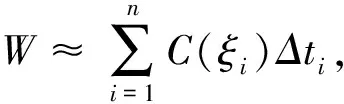
≈10.694

在教学中，利用此专业案例，可以使学生了解定积分在专业中的应用背景，理解定积分“分割、近似、求和、取极限”的重要思想，更能使学生掌握处理问题的方法，从而更好地把所学知识应用到专业问题及实际问题中。

(三)案例三：微分方程求解问题

在高等数学中，微分方程的定义引入是通过几何及物理学中的函数与导函数的关系式进行的。下面这个案例是纺织专业领域中运用微分方程解决的一类实际问题。

设U(t)为时刻t时织物的质量，那么织物的瞬时变化率为

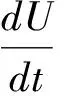
(2)

其中k表示织物上毛羽的抽拨率，如果在t=0时织物质量为U0，则方程(1)的解为U=U0exp(-kt)。对于织物起毛的初始阶段，即t→0时，U→U0，可将U=U0exp(-kt)等价于U=U0(1-kt)；当t→∞时，U→0。注意到，模型(2)中毛羽的变化率为常数，然而在现实生活中毛羽的变化率往往与时间有关，从而得到如下的修正模型

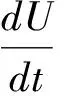
(3)

求解得

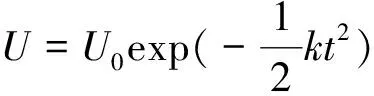
在教学中，可通过模型的一步步修正或考虑因素的增多，引导学生使用数学建模思维来思考专业问题。通过此案例，学生不仅了解了微分方程的概念，学会了方程的求解方法，了解了指数函数的线性近似方法，对提高学生的专业学习兴趣、拓宽学习思维模式大有裨益。

三、结束语

理工科高等数学教学过程中不仅需要教师有数学建模与数学实验教学经验，还需要教师对数学在所教专业中的应用有较为深刻的理解，并对该专业最新相关研究成果有所了解。此外，如何结合不同的专业特点和要求，在高等数学的教学中选择合适的教学内容和案例,也是开展数学建模的“融入”教学的一个重要研究方向[15]。