基于等级年龄结构种群模型的最优收获问题
夏洪涛,刘 炎
(中国计量大学 理学院,浙江 杭州 310018)
1926年内科医生A.G.McKendrick首次将年龄结构引进单种群动力学模型,McKendrick模型是将关于种群总数(或密度)的函数用时间和年龄两个变量来刻画。基于McKendrick模型的研究在过去几十年间成果丰富[1-9]。
传统的年龄结构种群模型研究工作对于出生率和死亡率主取决于年龄、时间,但是在许多生物种群中可以观察到在同一种群中个体之间的活动也会对生存率产生影响[10],虽然分层结构模型可以很好地模拟大多数生物物种,但是由于生物的出生率和死亡率是高阶非线性的,处理分层结构模型是具有挑战性的工作。
在最优收获问题上,基于年龄结构的研究成果丰富[11-15],从自然界种群内部之间的关系来看,等级年龄结构模型相对于年龄结构模型可以更好的描述自然界中的种群,畜牧业、渔业、林业等产业既要要求获得最大的经济效益,又要保证种群的可持续发展,如何使得这一矛盾达到平衡?即如何在保证生物种群可持续发展的同时使得养殖业达到最大的经济效益;基于此,本文主要研究基于等级年龄结构种群模型的最优收获问题。首先助特征线的方法求解基于等级年龄结构模型的最优收获问题的解及其性质并借助Banach不动点定理、Gronwall不等式研究解的相关性质。
1 最优收获模型
具有年龄结构种群模型的最优收获问题在过去几十年内得到充分研究,然而对于有些种群(森林、鱼类等)来说,等级年龄结构种群模型可以更好地描述种群的发展趋势,由于相对于传统的年龄结构模型,等级年龄结构考虑了个体之间的影响,基于此考虑等级年龄结构种群模型的最优收获问题:
(1)
这里,c(a)表示年龄为a的生物个体的经济效益,u(a,t)表示时间t对年龄为a的种群个体的收获力度且u∈U={u(a,t):u(a,t)∈L∞(Qt);ξ1(a,t)≤u(a,t)≤ξ2(a,t);ξi(a,t)≥0(i=1,2)},p(a,t)表示年龄a在t时刻的个体密度且p(a,t)满足:
(2)
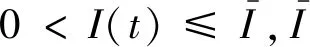

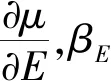
|β(a,s1)-β(a,s2)|≤L(M)|s1-s2|,
|μ(a,s1)-μ(a,s2)|≤L(M)|s1-s2|
对于所有满足有界条件的s1,s2均成立;
3)对于任意a∈(0,A),p0(a)非负有界;
4)c(a)∈C1(0,A),c(a)非负有界。
2 最优解存在性
定义3.1如果在每一条特征线t-a=h(h为常数)上p(a,t)都是绝对连续的,且满足以下条件,则称p(a,t)是模型(2)的解
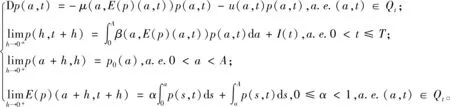
(3)
定理3.1存在性证明可以参见文献[15],此处从略,下证唯一性对于任意给定的u∈U,模型(2)存在唯一的解pu(a,t),且是非负有界的。
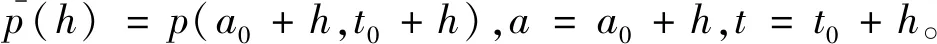
求解方程得到
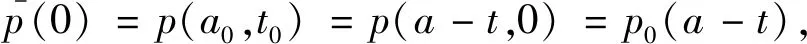
(4)
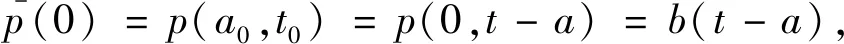
(5)
再由模型(2)对于t∈(0,T]
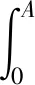
(6)
其中
由假设(1)—(4)可知K∈L∞(Qt),F∈L∞(0,T]且:
F(t)≥0,a.e.t∈(0,T];
K(t,a)≥0,a.e.(a,t)∈Qt。
(7)
选取λ>0,在L∞(0,T]上定义范数
定义映射

那么对于∀b1,b2∈L∞(0,T],有

其中||·||∞表示空间L∞(Qt)中的通常范数。那么当λ>||K||∞时,映射J是压缩映射,则存在唯一不动点,即式(6)存在唯一的解,再由式(4)(5)可知模型(2)存在唯一解p(a,t)。
下证非负有界性:
由不动点定理可知,式(6)的解b(t)亦可由以下迭代过程得到:
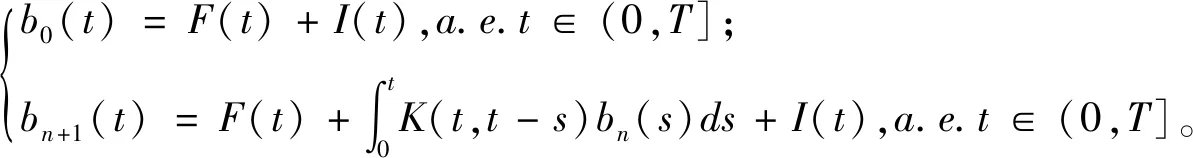
由上式可知序列{bn(t)}收敛于b(t),对于由(7)式可以得到{bn(t)}≥0a.e.t∈(0,T],借此推得b(t)≥0a.e.t∈(0,T],再由(4)(5)可知模型(2.1)的解p(a,t)非负。
根据式(6)可得
由Gronwall不等式推导可得
因此b(t)有是有界的,则模型p(a,t)是有界的,证毕。
定理3.2设模型(2)对应的解是pu(a,t),则:
1)如果u1(a,t)≥u2(a,t)a.e.(a,t)∈Qt,则pu1(a,t)≤pu2(a,t)a.e.(a,t)∈Qt;
2)如果在L∞(Qt),当n→∞时有un→u则在L∞(0,T;L1(0,A))上有pun→pu。
证明设φi(a,t,E(P)(a,t))=μ(a,E(P)(a,t))+ui(a,t)i=1,2,则由u1(a,t)≥u2(a,t)a.e.(a,t)∈Qt可得φ1(a,t,E(P)(a,t))≥φ2(a,t,E(P)(a,t))a.e.(a,t)∈Qt,由定理3.1证明过程可知,式(6)的解可以下迭代过程得到:
Fφ1(t)≤Fφ2(t),a.e.t∈(0,T];
(8)
由(7)式及φ1(a,t,E(P)(a,t))≥φ2(a,t,E(P)(a,t))a.e.(a,t)∈Qt,可得
再由(8)式能够得到bφ1(t)≤bφ2(t)a.e.t∈(0,T],再由(4)(5)易证定理3.2结论1)成立,下证结论2)成立。
记pun,pu分别为等级年龄结构收获模型(1)(2)相对应于收获函数un,u的解,在Qt上令
对于a≥t,有
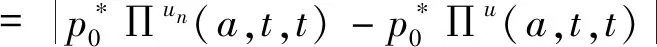
成立,其中M1是一个正常数。另一方面,存在正常数M2对于a |pun(a,t)-pu(a,t)|=|b(t-a)unun(a,t,a)-b(t-a)uu(a,t,a)| ≤|[b(t-a)un-b(t-a)u]un(a,t,a)|+|b(t-a)u[un(a,t,a)-u(a,t,a)]| 设z=t-a,在Qt上,由(6)可得 其中 这里 另一方面,存在正常数M3使得 综上所述,可以得到存在正常数M4、M5 再由Gronwall不等式可以推得 ||pun-pu||L∞(Qt)≤M6||un-u||∞。 其中M6是正常数且与pun,pu无关,则由不动点定理在L∞(Qt),当n→∞时有un→u在L∞(0,T;L1(0,A))上有pun→pu知结论2)成立,证毕。 本文主要研究基于等级年龄结构模型的最优问题的两个方面。运用特征线方法求解基于等级年龄结构种群模型的最优收获问题的解,借助Banach不动点定理、Gronwall不等式以及Bellman不等式证明了解的唯一性、非负性、有界性以及连续依赖性。本文进行解的相关性质的研究,基于此可以研究等级年龄结构种群模型的控制问题,即如何在保证可持续发展的同时获得最佳的经济效益。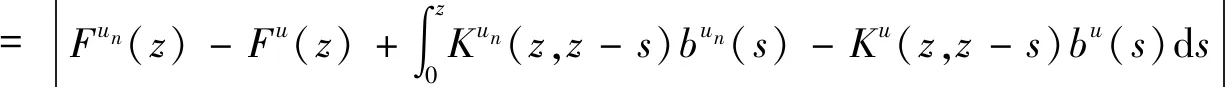
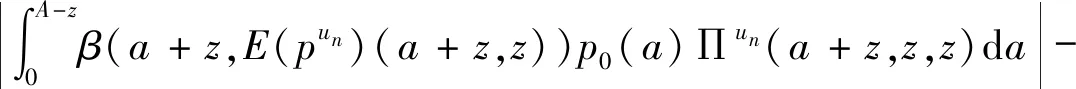

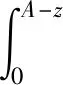
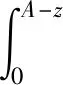
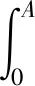



3 结 语

